How to find the area of an acute / obtuse triangle - Math

Card 1 of 164

0

Didn't Know

0

Didn't Know

Knew It

0

1 of 2019 left

Question

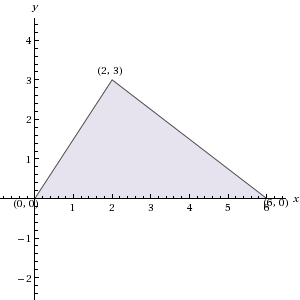
If triangle ABC has vertices (0, 0), (6, 0), and (2, 3) in the xy-plane, what is the area of ABC?

Tap to reveal answer

Answer

Sketching ABC in the xy-plane, as pictured here, we see that it has base 6 and height 3. Since the formula for the area of a triangle is 1/2 * base * height, the area of ABC is 1/2 * 6 * 3 = 9.

← Didn't Know|Knew It →

Question

The height, , of triangle in the figure is one-fourth the length of . In terms of h, what is the area of triangle ?

Tap to reveal answer

Answer

If h=\frac{1}{4}$ *$\overline{PQ}$, then the length of $\overline{PQ}$ must be 4h.

Using the formula for the area of a triangle ($\frac{1}{2}$bh), with b=4h, the area of the triangle must be $2h^{2}$.

← Didn't Know|Knew It →

Question

Find the area of a triangle whose base is and whose height is .

Tap to reveal answer

Answer

This problem is solved using the geometric formula for the area of a triangle.

$A=\frac{1}{2}$bh$

Convert feet to inches.

$\dpi{100} $\frac{2ft}{1}$$\frac{12in}{1ft}$=24in$

$A=\frac{1}{2}$14in24in$

← Didn't Know|Knew It →

Question

What is the area of a triangle with a height of and a base of ?

Tap to reveal answer

Answer

When searching for the area of a triangle we are looking for the amount of the space enclosed by the triangle.

The equation for area of a triangle is

Plug the values for base and height into the equation yielding

$$\frac{1}{2}$(4)(7)=Area$

Then multiply the numbers together to arrive at the answer .

← Didn't Know|Knew It →

Question

In ΔABC: a = 8, b = 13, c = 9.

Find the area of ΔABC (to the nearest tenth).

Tap to reveal answer

Answer

In order to determine the area of a non-right triangle, we can use Heron's formula:

$Area =$\sqrt{s(s-a)(s-b)(s-c)}$$
$s=\frac{a+b+c}{2}$$

Using the information from the question, we obtain:
$s=\frac{8+13+9}{2}$=15$
$Area =$\sqrt{15(15-8)(15-13)(15-9)}$=35.5$

← Didn't Know|Knew It →

Question

In ΔABC: a = 16, b = 11, c = 19.

Find the area of ΔABC (to the nearest tenth).

Tap to reveal answer

Answer

In order to determine the area of a non-right triangle, we can use Heron's formula:

$Area =$\sqrt{s(s-a)(s-b)(s-c)}$$
$s=\frac{a+b+c}{2}$$

Using the information from the question, we obtain:
$s=\frac{16+11+19}{2}$=23$
$Area =$\sqrt{23(23-16)(23-11)(23-19)}$=87.9$

← Didn't Know|Knew It →

Question

Find the height of a triangle if its base is long and its area is .

Tap to reveal answer

Answer

The formula to find the area of a triangle is

$$\text{Area}$=\frac{\text{base }$\times$\text{height}$}{2}$

Substitute in the given values for area and base to solve for the height, :

$24=\frac{12h}{2}$$

← Didn't Know|Knew It →

Question

In terms of , what is the area of a triangle with a height of and a base of ?

Tap to reveal answer

Answer

The formula to find the area of a triangle is

$\text{Area}$=\frac{base\times height}{2}$

Substitute in the given values for the base and the height to find the area.

$\text{Area}$=\frac{5a\times $2a}{2}$=\frac{10a^2$$}{2}$=5a^2$$:units^2$

← Didn't Know|Knew It →

Question

Find the area of the triangle below. Round to the nearest tenths place.

Tap to reveal answer

Answer

The formula used to find the area of the triangle is

$\text{Area}$=\frac{base\times height}{2}$

Now, we will need to use a trigonometric ratio to find the length of the height. Because of the angle given, we will need to use $\text{cosine}$ , because we are looking for the length of the adjacent side, the triangle's height, and we know the length of the hypotenuse of the smaller triangle formed by the height.

Remember that $\text{cosine }$\theta=\frac{adjacent}{hypotenuse}$

Now, solve for the height.

Now you can find the area of the triangle:

← Didn't Know|Knew It →

Question

Find the area of the triangle below. Round to the nearest tenths place.

Tap to reveal answer

Answer

The formula used to find the area of the triangle is

$\text{Area}$=\frac{base\times height}{2}$

Now, we will need to use a trigonometric ratio to find the length of the height. Because of the angle given, we will need to use $\text{cosine}$ , because we are looking for the length of the adjacent side, the triangle's height, and we know the length of the hypotenuse of the smaller triangle formed by the height.

Remember that $\text{cosine }$\theta=\frac{adjacent}{hypotenuse}$

Now, solve for the height.

Now you can find the area.

$\text{Area}$=\frac{45\times $10.05}{2}$=226.1:units^2$

← Didn't Know|Knew It →

Question

Find the area of the triangle below. Round to the nearest tenths place.

Tap to reveal answer

Answer

The formula used to find the area of the triangle is

$\text{Area}$=\frac{base\times height}{2}$

Now, we will need to use a trigonometric ratio to find the length of the height. Because of the angle given, we will need to use $\text{cosine}$ , because we are looking for the length of the adjacent side—the triangle's height—and we know the length of the hypotenuse of the smaller triangle formed by the height.

Remember that $\text{cosine }$\theta =\frac{adjacent}{hypotenuse}$

Now, solve for the height.

Now you can find the area.

$\text{Area}$=\frac{8\times $4.70}{2}$=18.8:units^2$

← Didn't Know|Knew It →

Question

Find the area of the triangle below. Round to the nearest tenths place.

Tap to reveal answer

Answer

The formula used to find the area of the triangle is

$\text{Area}$=\frac{base\times height}{2}$

Now, we will need to use a trigonometric ratio to find the length of the height. Because of the angle given, we will need to use $\text{cosine}$ , because we are looking for the length of the adjacent side—the triangle's height—and we know the length of the hypotenuse of the smaller triangle formed by the height.

Remember that $\text{cosine }$\theta=\frac{adjacent}{hypotenuse}$

Now, solve for the height.

Now you can find the area.

$\text{Area}$=\frac{7\times $2.85}{2}$=10.0:units^2$

← Didn't Know|Knew It →

Question

Find the area of the triangle below. Round to the nearest tenths place.

Tap to reveal answer

Answer

The formula used to find the area of the triangle is

$\text{Area}$=\frac{base\times height}{2}$

Now, we will need to use a trigonometric ratio to find the length of the height. Because of the angle given, we will need to use $\text{cosine}$ , because we are looking for the length of the adjacent side—the triangle's height—and we know the length of the hypotenuse of the smaller triangle formed by the height.

Remember that $\text{cosine }$\theta=\frac{adjacent}{hypotenuse}$

Now, solve for the height.

Now you can find the area.

$\text{Area}$=\frac{24\times $12.79}{2}$=153.5:units^2$

← Didn't Know|Knew It →

Question

Find the area of the triangle below. Round to the nearest tenths place.

Tap to reveal answer

Answer

The formula used to find the area of the triangle is

$\text{Area}$=\frac{base\times height}{2}$

Now, we will need to use a trigonometric ratio to find the length of the height. Because of the angle given, we will need to use $\text{sine}$ , because we are looking for the height of the triangle, which in this case is the side opposite to the known angle, and we also know the length of the hypotenuse of the smaller triangle formed by the height.

Remember that $\text{sin }$\theta=\frac{opposite}{hypotenuse}$

Now, solve for the height.

Now you can find the area.

$\text{Area}$=\frac{14\times $9.83}{2}$=68.8:units^2$

← Didn't Know|Knew It →

Question

Find the area of the triangle. Round to the nearest tenths.

Tap to reveal answer

Answer

The formula used to find the area of the triangle is

$\text{Area}$=\frac{base\times height}{2}$

Now, we will need to use a trigonometric ratio to find the length of the height. Because of the angle given, we will need to use $\text{sine}$ , because we are looking for the height of the triangle, which in this case is the side opposite to the known angle, and we also know the length of the hypotenuse of the smaller triangle formed by the height.

Remember that $\text{sin }$\theta=\frac{opposite}{hypotenuse}$

Now, solve for the height.

Now you can find the area.

$\text{Area}$=\frac{12\times $5.90}{2}$=35.4:units^2$

← Didn't Know|Knew It →

Question

Find the area of the triangle below. Round to the nearest tenths place.

Tap to reveal answer

Answer

The formula used to find the area of the triangle is

$\text{Area}$=\frac{base\times height}{2}$

Now, we will need to use a trigonometric ratio to find the length of the height. Because of the angle given, we will need to use $\text{sine}$ , because we are looking for the height of the triangle, which in this case is the side opposite to the known angle, and we also know the length of the hypotenuse of the smaller triangle formed by the height.

Remember that $\text{sin }$\theta=\frac{opposite}{hypotenuse}$

Now, solve for the height.

Now you can find the area.

$\text{Area}$=\frac{14\times $2.35}{2}$=16.5:units^2$

← Didn't Know|Knew It →

Question

Find the area of the triangle below. Round to the nearest tenths place.

Tap to reveal answer

Answer

The formula used to find the area of the triangle is

$\text{Area}$=\frac{base\times height}{2}$

Now, we will need to use a trigonometric ratio to find the length of the height. Because of the angle given, we will need to use $\text{sine}$ , because we are looking for the height of the triangle, which in this case is the side opposite to the known angle, and we also know the length of the hypotenuse of the smaller triangle formed by the height.

Remember that $\text{sin }$\theta=\frac{opposite}{hypotenuse}$

Now, solve for the height.

Now you can find the area.

$\text{Area}$=\frac{30\times $5.35}{2}$=80.3:units^2$

← Didn't Know|Knew It →

Question

Find the area of the triangle below. Round to the nearest tenths place.

Tap to reveal answer

Answer

The formula used to find the area of the triangle is

$\text{Area}$=\frac{base\times height}{2}$

Now, we will need to use a trigonometric ratio to find the length of the height. Because of the angle given, we will need to use $\text{sine}$ , because we are looking for the height of the triangle, which in this case is the side opposite to the known angle, and we also know the length of the hypotenuse of the smaller triangle formed by the height.

Remember that $\text{sin }$\theta=\frac{opposite}{hypotenuse}$

Now, solve for the height.

Now you can find the area.

$\text{Area}$=\frac{26\times $8.92}{2}$=116.0:units^2$

← Didn't Know|Knew It →

Question

In the figure, a triangle that shares its base with the width of the rectangle has a height that is half the length of the rectangle. Find the area of the shaded region.

Tap to reveal answer

Answer

In order to find the area of the shaded region, we must first find the areas of the triangle and the rectangle.

Recall how to find the area of a rectangle:

$\text{Area of Rectangle}$=$\text{length}$\times$\text{width}$

Substitute in the given length and width to find the area.

$$\text{Area of Rectangle}$=8 \times 12$

$$\text{Area of Rectangle}$= 96$

Next, recall how to find the area of a triangle:

$\text{Area of Triangle}$=\frac{1}{2}$\times$\text{base}$\times$\text{height}$

From the question, we know that the height of the triangle is half the length of the rectangle. Use the length of the rectangle to find the height of the triangle:

$$\text{height}$=\frac{\text{length}$}{2}$

$\text{height}$=\frac{8}{2}$

$$\text{height}$=4$

Since the base of the triangle and the width of the rectangle are the same, we can find the area of the triangle:

$$\text{Area of Triangle}$=\frac{1}{2}$\times 12\times 4$

$$\text{Area of Triangle}$=24$

To find the area of the shaded region, subtract the area of the triangle from the area of the rectangle.

$\text{Area of Shaded Region}$=$\text{Area of Rectangle}$-$\text{Area of Triangle}$

$$\text{Area of Shaded Region}$=96-24$

Solve.

$$\text{Area of Shaded Region}$=72$

← Didn't Know|Knew It →

Question

In the figure, a triangle that shares its base with the width of the rectangle has a height that is half the length of the rectangle. Find the area of the shaded region.

Tap to reveal answer

Answer

In order to find the area of the shaded region, we must first find the areas of the triangle and the rectangle.

Recall how to find the area of a rectangle:

$\text{Area of Rectangle}$=$\text{length}$\times$\text{width}$

Substitute in the given length and width to find the area.

$$\text{Area of Rectangle}$=6 \times 12$

$$\text{Area of Rectangle}$= 72$

Next, recall how to find the area of a triangle:

$\text{Area of Triangle}$=\frac{1}{2}$\times$\text{base}$\times$\text{height}$

From the question, we know that the height of the triangle is half the length of the rectangle. Use the length of the rectangle to find the height of the triangle:

$$\text{height}$=\frac{\text{length}$}{2}$

$\text{height}$=\frac{6}{2}$

$$\text{height}$=3$

Since the base of the triangle and the width of the rectangle are the same, we can find the area of the triangle:

$$\text{Area of Triangle}$=\frac{1}{2}$\times 12\times 3$

$$\text{Area of Triangle}$=18$

To find the area of the shaded region, subtract the area of the triangle from the area of the rectangle.

$\text{Area of Shaded Region}$=$\text{Area of Rectangle}$-$\text{Area of Triangle}$

$$\text{Area of Shaded Region}$=72-18$

Solve.

$$\text{Area of Shaded Region}$=54$

← Didn't Know|Knew It →

0

Knew It