How to find the area of a 45/45/90 right isosceles triangle - Math
Card 1 of 192
The base of a right isosceles triangle is 8 inches. The hypotenuse is not the base. What is the area of the triangle in inches?
The base of a right isosceles triangle is 8 inches. The hypotenuse is not the base. What is the area of the triangle in inches?
Tap to reveal answer
To find the area of a triangle, multiply the base by the height, then divide by 2. Since the short legs of an isosceles triangle are the same length, we need to know only one to know the other. Since, a short side serves as the base of the triangle, the other short side tells us the height.

To find the area of a triangle, multiply the base by the height, then divide by 2. Since the short legs of an isosceles triangle are the same length, we need to know only one to know the other. Since, a short side serves as the base of the triangle, the other short side tells us the height.
← Didn't Know|Knew It →
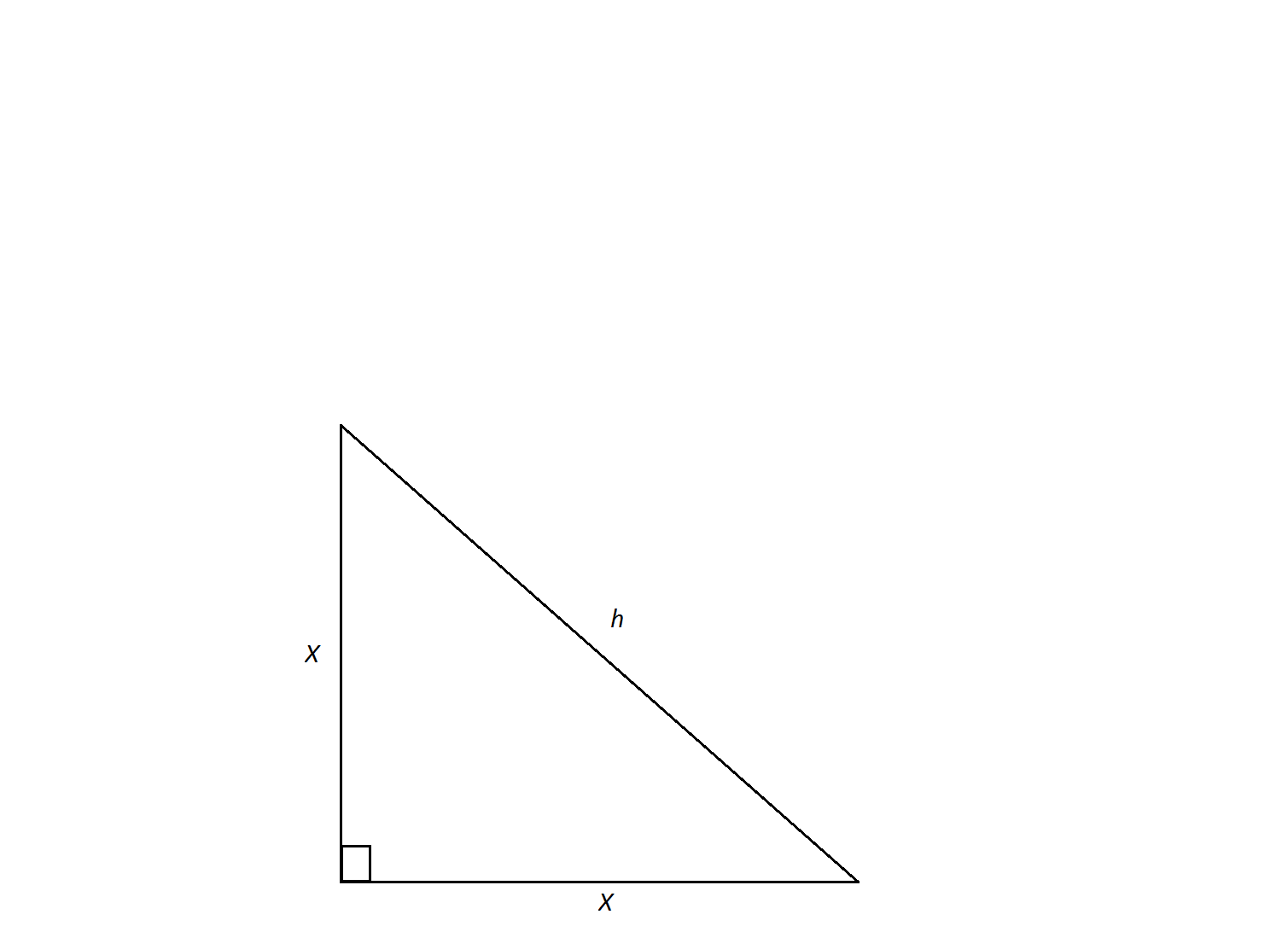
An isosceles right triangle has a hypotenuse of  . Find its area.
. Find its area.

An isosceles right triangle has a hypotenuse of 
Tap to reveal answer
In order to calculate the triangle's area, we need to find the lengths of its legs. An isosceles triangle is a special triangle due to the values of its angles. These triangles are referred to as  triangles and their side lengths follow a specific pattern that states that one can calculate the length of the legs of an isoceles triangle by dividing the length of the hypotenuse by the square root of 2.
triangles and their side lengths follow a specific pattern that states that one can calculate the length of the legs of an isoceles triangle by dividing the length of the hypotenuse by the square root of 2.

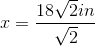

Now we can calculate the area using the formula



Now, convert to feet.

In order to calculate the triangle's area, we need to find the lengths of its legs. An isosceles triangle is a special triangle due to the values of its angles. These triangles are referred to as 
Now we can calculate the area using the formula
Now, convert to feet.
← Didn't Know|Knew It →
The base of a right isosceles triangle is 8 inches. The hypotenuse is not the base. What is the area of the triangle in inches?
The base of a right isosceles triangle is 8 inches. The hypotenuse is not the base. What is the area of the triangle in inches?
Tap to reveal answer
To find the area of a triangle, multiply the base by the height, then divide by 2. Since the short legs of an isosceles triangle are the same length, we need to know only one to know the other. Since, a short side serves as the base of the triangle, the other short side tells us the height.

To find the area of a triangle, multiply the base by the height, then divide by 2. Since the short legs of an isosceles triangle are the same length, we need to know only one to know the other. Since, a short side serves as the base of the triangle, the other short side tells us the height.
← Didn't Know|Knew It →

An isosceles right triangle has a hypotenuse of  . Find its area.
. Find its area.

An isosceles right triangle has a hypotenuse of 
Tap to reveal answer
In order to calculate the triangle's area, we need to find the lengths of its legs. An isosceles triangle is a special triangle due to the values of its angles. These triangles are referred to as  triangles and their side lengths follow a specific pattern that states that one can calculate the length of the legs of an isoceles triangle by dividing the length of the hypotenuse by the square root of 2.
triangles and their side lengths follow a specific pattern that states that one can calculate the length of the legs of an isoceles triangle by dividing the length of the hypotenuse by the square root of 2.

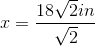

Now we can calculate the area using the formula



Now, convert to feet.

In order to calculate the triangle's area, we need to find the lengths of its legs. An isosceles triangle is a special triangle due to the values of its angles. These triangles are referred to as 
Now we can calculate the area using the formula
Now, convert to feet.
← Didn't Know|Knew It →

Tap to reveal answer
← Didn't Know|Knew It →
Consider an isosceles triangle with a height of 24 and a base of 12. What is the area of this triangle?

Consider an isosceles triangle with a height of 24 and a base of 12. What is the area of this triangle?

Tap to reveal answer
The formula for the area of a trianlge is A = base * height * (1/2).
We're lucky here, because the question gives us all of the values we need. We simply need to plug them in:
A = base * height * (1/2) = 12 * 24 * (1/2) = 12 * 12 = 144
The formula for the area of a trianlge is A = base * height * (1/2).
We're lucky here, because the question gives us all of the values we need. We simply need to plug them in:
A = base * height * (1/2) = 12 * 24 * (1/2) = 12 * 12 = 144
← Didn't Know|Knew It →
The side length of the 45-45-90 right triangle is  , find the area of the right triangle.
, find the area of the right triangle.
The side length of the 45-45-90 right triangle is 
Tap to reveal answer
The area of a triangle is:
 where b=base, h=height, and A=area
where b=base, h=height, and A=area

The area of a triangle is:

← Didn't Know|Knew It →
Calculate the area of an isosceles right triangle who's hypotenuse is  inches.
inches.
Calculate the area of an isosceles right triangle who's hypotenuse is 
Tap to reveal answer
The formula for the area of a triangle, right or not, is one half the base times height.
In this case, they are both  Therefore, the respective values are entered, yielding:
Therefore, the respective values are entered, yielding:

The formula for the area of a triangle, right or not, is one half the base times height.
In this case, they are both 
← Didn't Know|Knew It →
Find the area of the triangle below.

Find the area of the triangle below.

Tap to reveal answer
The key to finding the area of our triangle is to reaize that it is isosceles and therefore is a 45-45-90 triangle; therefore, we know the legs of our triangle are congruent and that each can be found by dividing the length of the hypotenuse by  .
.

Rationalizing the denominator simplifies our result; however, we are interested in the area, not just the length of a leg; we remember that the formula for the area of a triangle is

where  is the base and
is the base and  is the height; however, in our right triangle, the base and height are simply the two legs; therefore, we can calculate the area by substituting.
is the height; however, in our right triangle, the base and height are simply the two legs; therefore, we can calculate the area by substituting.

The key to finding the area of our triangle is to reaize that it is isosceles and therefore is a 45-45-90 triangle; therefore, we know the legs of our triangle are congruent and that each can be found by dividing the length of the hypotenuse by 
Rationalizing the denominator simplifies our result; however, we are interested in the area, not just the length of a leg; we remember that the formula for the area of a triangle is
where 

← Didn't Know|Knew It →
Find the area of a  triangle that has a hypotenuse of
triangle that has a hypotenuse of  .
.
Find the area of a 

Tap to reveal answer
To find the area of a triangle, we must use  where b=base and h=height.
where b=base and h=height.
In the problem, the only information given is what type the triangle is and what its hypotenuse is.
Given the area equation, the problem hasn't given any numbers that can be substituted into the equation to solve for an area. This means that the hypotenuse value must be used to determine the height and the base.
Because this is a 45/45/90 triangle, this means that it is also isosceles. Therefore, we can logic out that the base and the height must be the same.
The missing sides can be calulated in one of two ways:
1. Using the Pythagorean Theorem 
2. Or using 
If we were to use the Pythagorean Theorem, since we've already determined that b=h, that mean a=b in the equation. Let's say that  .
.
That means the Pythagorean Theorem can be rewritten as:


Now to substitute in the value of c to solve for the height and base.






Now that we have the base and the height, we can substitute the values into the area equation and get the triangle's area.




To find the area of a triangle, we must use 
In the problem, the only information given is what type the triangle is and what its hypotenuse is.
Given the area equation, the problem hasn't given any numbers that can be substituted into the equation to solve for an area. This means that the hypotenuse value must be used to determine the height and the base.
Because this is a 45/45/90 triangle, this means that it is also isosceles. Therefore, we can logic out that the base and the height must be the same.
The missing sides can be calulated in one of two ways:
1. Using the Pythagorean Theorem
2. Or using
If we were to use the Pythagorean Theorem, since we've already determined that b=h, that mean a=b in the equation. Let's say that 
That means the Pythagorean Theorem can be rewritten as:
Now to substitute in the value of c to solve for the height and base.
Now that we have the base and the height, we can substitute the values into the area equation and get the triangle's area.
← Didn't Know|Knew It →
Find the area of a  triangle with a hypotenuse of
triangle with a hypotenuse of  .
.
Find the area of a 

Tap to reveal answer
To find the area of a triangle, we must use  where b=base and h=height.
where b=base and h=height.
In the problem, the only information given is what type the triangle is and what its hypotenuse is.
Given the area equation, the problem hasn't given any numbers that can be substituted into the equation to solve for an area. This means that the hypotenuse value must be used to determine the height and the base.
Because this is a 45/45/90 triangle, this means that it is also isosceles. Therefore, we can logic out that the base and the height must be the same.
The missing sides can be calulated in one of two ways:
1. Using the Pythagorean Theorem 
2. Or using 
If we were to use the Pythagorean Theorem, since we've already determined that b=h, that means a=b in the equation. Let's say that  .
.
That means the Pythagorean Theorem can be rewritten as:


Now to substitute in the value of c to solve for the height and base.






Now that we have the base and the height, we can substitute the values into the area equation and get the triangle's area.



To find the area of a triangle, we must use 
In the problem, the only information given is what type the triangle is and what its hypotenuse is.
Given the area equation, the problem hasn't given any numbers that can be substituted into the equation to solve for an area. This means that the hypotenuse value must be used to determine the height and the base.
Because this is a 45/45/90 triangle, this means that it is also isosceles. Therefore, we can logic out that the base and the height must be the same.
The missing sides can be calulated in one of two ways:
1. Using the Pythagorean Theorem
2. Or using
If we were to use the Pythagorean Theorem, since we've already determined that b=h, that means a=b in the equation. Let's say that 
That means the Pythagorean Theorem can be rewritten as:
Now to substitute in the value of c to solve for the height and base.
Now that we have the base and the height, we can substitute the values into the area equation and get the triangle's area.
← Didn't Know|Knew It →
If the hypotenuse of an isosceles right triangle is  cm, what is the area of the triangle in square centimeters?
cm, what is the area of the triangle in square centimeters?

If the hypotenuse of an isosceles right triangle is 

Tap to reveal answer
Isosceles right triangles are special triangles because they possess angles of the following measures:  ,
,  , and
, and  . These triangles are known as 45-45-90 triangles and have special characteristics. Recall the Pythagorean theorem:
. These triangles are known as 45-45-90 triangles and have special characteristics. Recall the Pythagorean theorem:

In this equation,  is the length of the triangle's base,
is the length of the triangle's base,  is equal to its height, and
is equal to its height, and  is equal to the length of its hypotenuse. In an isosceles right triangle, the base and the height have the same length; therefore,
is equal to the length of its hypotenuse. In an isosceles right triangle, the base and the height have the same length; therefore,  is equal to
is equal to  , and you can rewrite the Pythagorean theorem like this:
, and you can rewrite the Pythagorean theorem like this:

Rearrange the equation so that  is isolated on one side of the equals sign. First, simplify by dividing both sides of the equation by 2.
is isolated on one side of the equals sign. First, simplify by dividing both sides of the equation by 2.


Next, take the square root of both sides.


Now, plug in the value of the hypotenuse to find the height/base of the given triangle.


Now, recall how to find the area of a triangle:

Since the base and the height are the same length, we can find the area of the given triangle.


Solve.

Isosceles right triangles are special triangles because they possess angles of the following measures: 


In this equation, 




Rearrange the equation so that 
Next, take the square root of both sides.
Now, plug in the value of the hypotenuse to find the height/base of the given triangle.
Now, recall how to find the area of a triangle:
Since the base and the height are the same length, we can find the area of the given triangle.
Solve.
← Didn't Know|Knew It →
If the hypotenuse of an isosceles right triangle is  , what is the area of the triangle?
, what is the area of the triangle?
If the hypotenuse of an isosceles right triangle is 
Tap to reveal answer
An isosceles right triangle is another way of saying that the triangle is a  triangle.
triangle.

Now, recall the Pythagorean Theorem:

Because we are working with a  triangle, the base and the height have the same length. We can rewrite the above equation as the following:
triangle, the base and the height have the same length. We can rewrite the above equation as the following:




Now, plug in the value of the hypotenuse to find the height for the given triangle.

Now, recall how to find the area of a triangle:

Since the base and the height are the same length, we can then find the area of the given triangle.

An isosceles right triangle is another way of saying that the triangle is a 

Now, recall the Pythagorean Theorem:
Because we are working with a 
Now, plug in the value of the hypotenuse to find the height for the given triangle.
Now, recall how to find the area of a triangle:
Since the base and the height are the same length, we can then find the area of the given triangle.
← Didn't Know|Knew It →
If the hypotenuse of an isosceles right triangle is  , what is the area of the triangle?
, what is the area of the triangle?
If the hypotenuse of an isosceles right triangle is 
Tap to reveal answer
An isosceles right triangle is another way of saying that the triangle is a  triangle.
triangle.

Now, recall the Pythagorean Theorem:

Because we are working with a  triangle, the base and the height have the same length. We can rewrite the above equation as the following:
triangle, the base and the height have the same length. We can rewrite the above equation as the following:




Now, plug in the value of the hypotenuse to find the height for the given triangle.

Now, recall how to find the area of a triangle:

Since the base and the height are the same length, we can then find the area of the given triangle.

An isosceles right triangle is another way of saying that the triangle is a 

Now, recall the Pythagorean Theorem:
Because we are working with a 
Now, plug in the value of the hypotenuse to find the height for the given triangle.
Now, recall how to find the area of a triangle:
Since the base and the height are the same length, we can then find the area of the given triangle.
← Didn't Know|Knew It →
If the hypotenuse of an isosceles right triangle is  , what is the area of the triangle?
, what is the area of the triangle?
If the hypotenuse of an isosceles right triangle is 
Tap to reveal answer
An isosceles right triangle is another way of saying that the triangle is a  triangle.
triangle.

Now, recall the Pythagorean Theorem:

Because we are working with a  triangle, the base and the height have the same length. We can rewrite the above equation as the following:
triangle, the base and the height have the same length. We can rewrite the above equation as the following:




Now, plug in the value of the hypotenuse to find the height for the given triangle.

Now, recall how to find the area of a triangle:

Since the base and the height are the same length, we can then find the area of the given triangle.

An isosceles right triangle is another way of saying that the triangle is a 

Now, recall the Pythagorean Theorem:
Because we are working with a 
Now, plug in the value of the hypotenuse to find the height for the given triangle.
Now, recall how to find the area of a triangle:
Since the base and the height are the same length, we can then find the area of the given triangle.
← Didn't Know|Knew It →
If the hypotenuse of a right isosceles triangle is  , what is the area of the triangle?
, what is the area of the triangle?
If the hypotenuse of a right isosceles triangle is 
Tap to reveal answer
An isosceles right triangle is another way of saying that the triangle is a  triangle.
triangle.

Now, recall the Pythagorean Theorem:

Because we are working with a  triangle, the base and the height have the same length. We can rewrite the above equation as the following:
triangle, the base and the height have the same length. We can rewrite the above equation as the following:




Now, plug in the value of the hypotenuse to find the height for the given triangle.

Now, recall how to find the area of a triangle:

Since the base and the height are the same length, we can then find the area of the given triangle.

An isosceles right triangle is another way of saying that the triangle is a 

Now, recall the Pythagorean Theorem:
Because we are working with a 
Now, plug in the value of the hypotenuse to find the height for the given triangle.
Now, recall how to find the area of a triangle:
Since the base and the height are the same length, we can then find the area of the given triangle.
← Didn't Know|Knew It →
If the hypotenuse of a right isosceles triangle is  , what is the area of the triangle?
, what is the area of the triangle?
If the hypotenuse of a right isosceles triangle is 
Tap to reveal answer
An isosceles right triangle is another way of saying that the triangle is a  triangle.
triangle.

Now, recall the Pythagorean Theorem:

Because we are working with a  triangle, the base and the height have the same length. We can rewrite the above equation as the following:
triangle, the base and the height have the same length. We can rewrite the above equation as the following:




Now, plug in the value of the hypotenuse to find the height for the given triangle.

Now, recall how to find the area of a triangle:

Since the base and the height are the same length, we can then find the area of the given triangle.

An isosceles right triangle is another way of saying that the triangle is a 

Now, recall the Pythagorean Theorem:
Because we are working with a 
Now, plug in the value of the hypotenuse to find the height for the given triangle.
Now, recall how to find the area of a triangle:
Since the base and the height are the same length, we can then find the area of the given triangle.
← Didn't Know|Knew It →
If the hypotenuse of a right isosceles triangle is  , what is the area of the triangle?
, what is the area of the triangle?
If the hypotenuse of a right isosceles triangle is 
Tap to reveal answer
An isosceles right triangle is another way of saying that the triangle is a  triangle.
triangle.

Now, recall the Pythagorean Theorem:

Because we are working with a  triangle, the base and the height have the same length. We can rewrite the above equation as the following:
triangle, the base and the height have the same length. We can rewrite the above equation as the following:




Now, plug in the value of the hypotenuse to find the height for the given triangle.

Now, recall how to find the area of a triangle:

Since the base and the height are the same length, we can then find the area of the given triangle.

An isosceles right triangle is another way of saying that the triangle is a 

Now, recall the Pythagorean Theorem:
Because we are working with a 
Now, plug in the value of the hypotenuse to find the height for the given triangle.
Now, recall how to find the area of a triangle:
Since the base and the height are the same length, we can then find the area of the given triangle.
← Didn't Know|Knew It →
If the hypotenuse of a right isosceles triangle is  , what is the area of the triangle?
, what is the area of the triangle?
If the hypotenuse of a right isosceles triangle is 
Tap to reveal answer
An isosceles right triangle is another way of saying that the triangle is a  triangle.
triangle.

Now, recall the Pythagorean Theorem:

Because we are working with a  triangle, the base and the height have the same length. We can rewrite the above equation as the following:
triangle, the base and the height have the same length. We can rewrite the above equation as the following:




Now, plug in the value of the hypotenuse to find the height for the given triangle.

Now, recall how to find the area of a triangle:

Since the base and the height are the same length, we can then find the area of the given triangle.

An isosceles right triangle is another way of saying that the triangle is a 

Now, recall the Pythagorean Theorem:
Because we are working with a 
Now, plug in the value of the hypotenuse to find the height for the given triangle.
Now, recall how to find the area of a triangle:
Since the base and the height are the same length, we can then find the area of the given triangle.
← Didn't Know|Knew It →
If the hypotenuse of a right isosceles triangle is  , what is the area of the triangle?
, what is the area of the triangle?
If the hypotenuse of a right isosceles triangle is 
Tap to reveal answer
An isosceles right triangle is another way of saying that the triangle is a  triangle.
triangle.

Now, recall the Pythagorean Theorem:

Because we are working with a  triangle, the base and the height have the same length. We can rewrite the above equation as the following:
triangle, the base and the height have the same length. We can rewrite the above equation as the following:




Now, plug in the value of the hypotenuse to find the height for the given triangle.

Now, recall how to find the area of a triangle:

Since the base and the height are the same length, we can then find the area of the given triangle.

An isosceles right triangle is another way of saying that the triangle is a 

Now, recall the Pythagorean Theorem:
Because we are working with a 
Now, plug in the value of the hypotenuse to find the height for the given triangle.
Now, recall how to find the area of a triangle:
Since the base and the height are the same length, we can then find the area of the given triangle.
← Didn't Know|Knew It →













