Quadratic Functions - Math
Card 1 of 76
A parabola is one example of a quadratic function, regardless of whether it points upwards or downwards.
The red line represents a quadratic function and will have a formula similar to  .
.
The blue line represents a linear function and will have a formula similar to  .
.
The green line represents an exponential function and will have a formula similar to  .
.
The purple line represents an absolute value function and will have a formula similar to  .
.
A parabola is one example of a quadratic function, regardless of whether it points upwards or downwards.
The red line represents a quadratic function and will have a formula similar to 
The blue line represents a linear function and will have a formula similar to 
The green line represents an exponential function and will have a formula similar to 
The purple line represents an absolute value function and will have a formula similar to 
← Didn't Know|Knew It →
Which of the following functions represents a parabola?
Which of the following functions represents a parabola?
Tap to reveal answer
A parabola is a curve that can be represented by a quadratic equation. The only quadratic here is represented by the function  , while the others represent straight lines, circles, and other curves.
, while the others represent straight lines, circles, and other curves.
A parabola is a curve that can be represented by a quadratic equation. The only quadratic here is represented by the function 
← Didn't Know|Knew It →
Find the  -intercepts for the circle given by the equation:
-intercepts for the circle given by the equation:

Find the 
Tap to reveal answer
To find the  -intercepts (where the graph crosses the
-intercepts (where the graph crosses the  -axis), we must set
-axis), we must set  . This gives us the equation:
. This gives us the equation:

Because the left side of the equation is squared, it will always give us a positive answer. Thus if we want to take the root of both sides, we must account for this by setting up two scenarios, one where the value inside of the parentheses is positive and one where it is negative. This gives us the equations:
 and
and 
We can then solve these two equations to obtain  .
.
To find the 


Because the left side of the equation is squared, it will always give us a positive answer. Thus if we want to take the root of both sides, we must account for this by setting up two scenarios, one where the value inside of the parentheses is positive and one where it is negative. This gives us the equations:

We can then solve these two equations to obtain 
← Didn't Know|Knew It →
Find the  -intercepts for the circle given by the equation:
-intercepts for the circle given by the equation:

Find the 
Tap to reveal answer
To find the  -intercepts (where the graph crosses the
-intercepts (where the graph crosses the  -axis), we must set
-axis), we must set  . This gives us the equation:
. This gives us the equation:


Because the left side of the equation is squared, it will always give us a positive answer. Thus if we want to take the root of both sides, we must account for this by setting up two scenarios, one where the value inside of the parentheses is positive and one where it is negative. This gives us the equations:
 and
and 
We can then solve these two equations to obtain
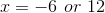
To find the 


Because the left side of the equation is squared, it will always give us a positive answer. Thus if we want to take the root of both sides, we must account for this by setting up two scenarios, one where the value inside of the parentheses is positive and one where it is negative. This gives us the equations:

We can then solve these two equations to obtain
← Didn't Know|Knew It →
Find the  -intercepts for the circle given by the equation:
-intercepts for the circle given by the equation:

Find the 
Tap to reveal answer
To find the  -intercepts (where the graph crosses the
-intercepts (where the graph crosses the  -axis), we must set
-axis), we must set  . This gives us the equation:
. This gives us the equation:

Because the left side of the equation is squared, it will always give us a positive answer. Thus if we want to take the root of both sides, we must account for this by setting up two scenarios, one where the value inside of the parentheses is positive and one where it is negative. This gives us the equations:
 and
and 
We can then solve these two equations to obtain  .
.
To find the 


Because the left side of the equation is squared, it will always give us a positive answer. Thus if we want to take the root of both sides, we must account for this by setting up two scenarios, one where the value inside of the parentheses is positive and one where it is negative. This gives us the equations:

We can then solve these two equations to obtain 
← Didn't Know|Knew It →
Find the  -intercepts for the circle given by the equation:
-intercepts for the circle given by the equation:

Find the 
Tap to reveal answer
To find the  -intercepts (where the graph crosses the
-intercepts (where the graph crosses the  -axis), we must set
-axis), we must set  . This gives us the equation:
. This gives us the equation:


Because the left side of the equation is squared, it will always give us a positive answer. Thus if we want to take the root of both sides, we must account for this by setting up two scenarios, one where the value inside of the parentheses is positive and one where it is negative. This gives us the equations:
 and
and 
We can then solve these two equations to obtain
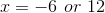
To find the 


Because the left side of the equation is squared, it will always give us a positive answer. Thus if we want to take the root of both sides, we must account for this by setting up two scenarios, one where the value inside of the parentheses is positive and one where it is negative. This gives us the equations:

We can then solve these two equations to obtain
← Didn't Know|Knew It →
Find the center and radius of the circle defined by the equation:

Find the center and radius of the circle defined by the equation:
Tap to reveal answer
The equation of a circle is:  where
where  is the radius and
is the radius and  is the center.
is the center.
In this problem, the equation is already in the format required to determine center and radius. To find the  -coordinate of the center, we must find the value of
-coordinate of the center, we must find the value of  that makes
that makes  equal to 0, which is 3. We do the same to find the y-coordinate of the center and find that
equal to 0, which is 3. We do the same to find the y-coordinate of the center and find that  . To find the radius we take the square root of the constant on the right side of the equation which is 6.
. To find the radius we take the square root of the constant on the right side of the equation which is 6.
The equation of a circle is: 


In this problem, the equation is already in the format required to determine center and radius. To find the 



← Didn't Know|Knew It →
Find the center and radius of the circle defined by the equation:

Find the center and radius of the circle defined by the equation:
Tap to reveal answer
The equation of a circle is:  where
where  is the radius and
is the radius and  is the center.
is the center.
In this problem, the equation is already in the format required to determine center and radius. To find the  -coordinate of the center, we must find the value of
-coordinate of the center, we must find the value of  that makes
that makes  equal to
equal to  , which is
, which is  . We do the same to find the y-coordinate of the center and find that
. We do the same to find the y-coordinate of the center and find that  . To find the radius we take the square root of the constant on the right side of the equation which is 10.
. To find the radius we take the square root of the constant on the right side of the equation which is 10.
The equation of a circle is: 


In this problem, the equation is already in the format required to determine center and radius. To find the 





← Didn't Know|Knew It →
Find the radius of the circle given by the equation:

Find the radius of the circle given by the equation:
Tap to reveal answer
To find the center or the radius of a circle, first put the equation in the standard form for a circle:  , where
, where  is the radius and
is the radius and  is the center.
is the center.
From our equation, we see that it has not yet been factored, so we must do that now. We can use the formula  .
.
 , so
, so  .
.
 and
and  , so
, so  and
and  .
.
Therefore,  .
.
Because the constant, in this case 4, was not in the original equation, we need to add it to both sides:



Now we do the same for  :
:


We can now find  :
:

To find the center or the radius of a circle, first put the equation in the standard form for a circle: 


From our equation, we see that it has not yet been factored, so we must do that now. We can use the formula 






Therefore, 
Because the constant, in this case 4, was not in the original equation, we need to add it to both sides:
Now we do the same for 
We can now find 
← Didn't Know|Knew It →
Find the center of the circle given by the equation:

Find the center of the circle given by the equation:
Tap to reveal answer
To find the center or the radius of a circle, first put the equation in standard form:  , where
, where  is the radius and
is the radius and  is the center.
is the center.
From our equation, we see that it has not yet been factored, so we must do that now. We can use the formula  .
.
 , so
, so  .
.
 and
and  , so
, so  and
and  .
.
This gives  .
.
Because the constant, in this case 9, was not in the original equation, we must add it to both sides:



Now we do the same for  :
:


We can now find the center: (3, -9)
To find the center or the radius of a circle, first put the equation in standard form: 


From our equation, we see that it has not yet been factored, so we must do that now. We can use the formula 






This gives 
Because the constant, in this case 9, was not in the original equation, we must add it to both sides:
Now we do the same for 
We can now find the center: (3, -9)
← Didn't Know|Knew It →
The graph of the equation

is a circle with what as the length of its radius?
The graph of the equation
is a circle with what as the length of its radius?
Tap to reveal answer
Rewrite the equation of the circle in standard form

as follows:


Since  and
and  , we complete the squares by adding:
, we complete the squares by adding:


The standard form of the equation sets
 ,
,
so the radius of the circle is

Rewrite the equation of the circle in standard form
as follows:
Since 

The standard form of the equation sets

so the radius of the circle is
← Didn't Know|Knew It →
Determine the graph of the equation

Determine the graph of the equation
Tap to reveal answer
The equation of a circle in standard for is:

Where the center  and the radius of the cirlce is
and the radius of the cirlce is  .
.
Dividing by 4 on both sides of the equation yields

or

an equation whose graph is a circle, centered at (2,3) with radius = .5
The equation of a circle in standard for is:
Where the center 

Dividing by 4 on both sides of the equation yields
or
an equation whose graph is a circle, centered at (2,3) with radius = .5
← Didn't Know|Knew It →
Give the radius and the center of the circle for the equation below.

Give the radius and the center of the circle for the equation below.
Tap to reveal answer
Look at the formula for the equation of a circle below.

Here  is the center and
is the center and  is the radius. Notice that the subtraction in the center is part of the formula. Thus, looking at our equation it is clear that the center is
is the radius. Notice that the subtraction in the center is part of the formula. Thus, looking at our equation it is clear that the center is  and the radius squared is
and the radius squared is  . When we square root this value we get that the radius must be
. When we square root this value we get that the radius must be  .
.
Look at the formula for the equation of a circle below.
Here 




← Didn't Know|Knew It →
Determine the equation of a circle whose center lies at the point  and has a radius of
and has a radius of  .
.
Determine the equation of a circle whose center lies at the point 

Tap to reveal answer
The equation for a circle with center  and radius
and radius  is :
is :

Our circle is centered at  with radius
with radius  , so the equation for this circle is :
, so the equation for this circle is :

The equation for a circle with center 

Our circle is centered at 

← Didn't Know|Knew It →

What is the radius of the circle?
What is the radius of the circle?
Tap to reveal answer
The parent equation of a circle is represented by  . The radius of the circle is equal to
. The radius of the circle is equal to  . The radius of the cirle is
. The radius of the cirle is  .
.
The parent equation of a circle is represented by 


← Didn't Know|Knew It →
What is the center of the circle expressed by the funciton  ?
?
What is the center of the circle expressed by the funciton 
Tap to reveal answer
The equation can be rewritten so that it looks like the parent equation for a circle  . After completeing the square, the equation changes from
. After completeing the square, the equation changes from  to
to  . From there it can be expressed as
. From there it can be expressed as  . Therefore the center of the circle is at
. Therefore the center of the circle is at  .
.
The equation can be rewritten so that it looks like the parent equation for a circle 




← Didn't Know|Knew It →
What are the coordinates of the center of a circle with the equation  ?
?
What are the coordinates of the center of a circle with the equation 
Tap to reveal answer
The equation of a circle is  , in which (h, k) is the center of the circle. To derive the center of a circle from its equation, identify the constants immediately following x and y, and flip their signs. In the given equation, x is followed by -1 and y is followed by -6, so the coordinates of the center must be (1, 6).
, in which (h, k) is the center of the circle. To derive the center of a circle from its equation, identify the constants immediately following x and y, and flip their signs. In the given equation, x is followed by -1 and y is followed by -6, so the coordinates of the center must be (1, 6).
The equation of a circle is 
← Didn't Know|Knew It →
What is the radius of a circle with the equation  ?
?
What is the radius of a circle with the equation 
Tap to reveal answer
To convert the given equation into the format  , complete the square by adding
, complete the square by adding  to the x-terms and to the y-terms.
to the x-terms and to the y-terms.




The square root of 4 is 2, so the radius of the circle is 2.
To convert the given equation into the format 

The square root of 4 is 2, so the radius of the circle is 2.
← Didn't Know|Knew It →
What is the radius of a circle with the equation  ?
?
What is the radius of a circle with the equation 
Tap to reveal answer
To convert the given equation into the format  , complete the square by adding
, complete the square by adding  to the x-terms and to the y-terms.
to the x-terms and to the y-terms.




The square root of 25 is 5, so the radius of the circle is 5.
To convert the given equation into the format 

The square root of 25 is 5, so the radius of the circle is 5.
← Didn't Know|Knew It →
Which equation does this graph represent?

Which equation does this graph represent?

Tap to reveal answer
The equation of a circle is  , in which (h, k) is the center of the circle and r is its radius. Because the graph of the circle is centered at (0, 0), h and k are both 0. Because the radius is 3, the right side of the equation is equal to 9.
, in which (h, k) is the center of the circle and r is its radius. Because the graph of the circle is centered at (0, 0), h and k are both 0. Because the radius is 3, the right side of the equation is equal to 9.
The equation of a circle is 
← Didn't Know|Knew It →








