Finding Zeros of a Polynomial - Math
Card 1 of 92
Find the zeros of the following polynomial:

Find the zeros of the following polynomial:
Tap to reveal answer
First, we need to find all the possible rational roots of the polynomial using the Rational Roots Theorem:

Since the leading coefficient is just 1, we have the following possible (rational) roots to try:
±1, ±2, ±3, ±4, ±6, ±12, ±24
When we substitute one of these numbers for  , we're hoping that the equation ends up equaling zero. Let's see if
, we're hoping that the equation ends up equaling zero. Let's see if  is a zero:
is a zero:
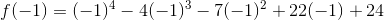


Since the function equals zero when  is
is  , one of the factors of the polynomial is
, one of the factors of the polynomial is  . This doesn't help us find the other factors, however. We can use synthetic substitution as a shorter way than long division to factor the equation.
. This doesn't help us find the other factors, however. We can use synthetic substitution as a shorter way than long division to factor the equation.



Now we can factor the function this way:
(x%5E%7B3%7D-5x%5E%7B2%7D-2x+24) $"f(x)=(x+1)(x^{3}$$-5x^{2}$-2x+24)")
We repeat this process, using the Rational Roots Theorem with the second term to find a possible zero. Let's try  :
:
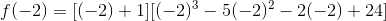

When we factor using synthetic substitution for  , we get the following result:
, we get the following result:

Using our quadratic factoring rules, we can factor completely:

Thus, the zeroes of  are
are 
First, we need to find all the possible rational roots of the polynomial using the Rational Roots Theorem:
Since the leading coefficient is just 1, we have the following possible (rational) roots to try:
±1, ±2, ±3, ±4, ±6, ±12, ±24
When we substitute one of these numbers for 

Since the function equals zero when 


Now we can factor the function this way:
(x%5E%7B3%7D-5x%5E%7B2%7D-2x+24) $"f(x)=(x+1)(x^{3}$$-5x^{2}$-2x+24)")
We repeat this process, using the Rational Roots Theorem with the second term to find a possible zero. Let's try 
When we factor using synthetic substitution for 
Using our quadratic factoring rules, we can factor completely:
Thus, the zeroes of 
← Didn't Know|Knew It →
Find the zeros of the following polynomial:

Find the zeros of the following polynomial:
Tap to reveal answer
First, we need to find all the possible rational roots of the polynomial using the Rational Roots Theorem:

Since the leading coefficient is just 1, we have the following possible (rational) roots to try:
±1, ±2, ±3, ±4, ±6, ±12, ±24
When we substitute one of these numbers for  , we're hoping that the equation ends up equaling zero. Let's see if
, we're hoping that the equation ends up equaling zero. Let's see if  is a zero:
is a zero:
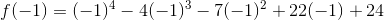


Since the function equals zero when  is
is  , one of the factors of the polynomial is
, one of the factors of the polynomial is  . This doesn't help us find the other factors, however. We can use synthetic substitution as a shorter way than long division to factor the equation.
. This doesn't help us find the other factors, however. We can use synthetic substitution as a shorter way than long division to factor the equation.



Now we can factor the function this way:
(x%5E%7B3%7D-5x%5E%7B2%7D-2x+24) $"f(x)=(x+1)(x^{3}$$-5x^{2}$-2x+24)")
We repeat this process, using the Rational Roots Theorem with the second term to find a possible zero. Let's try  :
:
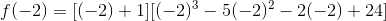

When we factor using synthetic substitution for  , we get the following result:
, we get the following result:

Using our quadratic factoring rules, we can factor completely:

Thus, the zeroes of  are
are 
First, we need to find all the possible rational roots of the polynomial using the Rational Roots Theorem:
Since the leading coefficient is just 1, we have the following possible (rational) roots to try:
±1, ±2, ±3, ±4, ±6, ±12, ±24
When we substitute one of these numbers for 

Since the function equals zero when 


Now we can factor the function this way:
(x%5E%7B3%7D-5x%5E%7B2%7D-2x+24) $"f(x)=(x+1)(x^{3}$$-5x^{2}$-2x+24)")
We repeat this process, using the Rational Roots Theorem with the second term to find a possible zero. Let's try 
When we factor using synthetic substitution for 
Using our quadratic factoring rules, we can factor completely:
Thus, the zeroes of 
← Didn't Know|Knew It →
Find the zeros of the following polynomial:

Find the zeros of the following polynomial:
Tap to reveal answer
First, we need to find all the possible rational roots of the polynomial using the Rational Roots Theorem:

Since the leading coefficient is just 1, we have the following possible (rational) roots to try:
±1, ±2, ±3, ±4, ±6, ±12, ±24
When we substitute one of these numbers for  , we're hoping that the equation ends up equaling zero. Let's see if
, we're hoping that the equation ends up equaling zero. Let's see if  is a zero:
is a zero:
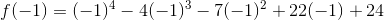


Since the function equals zero when  is
is  , one of the factors of the polynomial is
, one of the factors of the polynomial is  . This doesn't help us find the other factors, however. We can use synthetic substitution as a shorter way than long division to factor the equation.
. This doesn't help us find the other factors, however. We can use synthetic substitution as a shorter way than long division to factor the equation.



Now we can factor the function this way:
(x%5E%7B3%7D-5x%5E%7B2%7D-2x+24) $"f(x)=(x+1)(x^{3}$$-5x^{2}$-2x+24)")
We repeat this process, using the Rational Roots Theorem with the second term to find a possible zero. Let's try  :
:
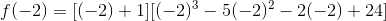

When we factor using synthetic substitution for  , we get the following result:
, we get the following result:

Using our quadratic factoring rules, we can factor completely:

Thus, the zeroes of  are
are 
First, we need to find all the possible rational roots of the polynomial using the Rational Roots Theorem:
Since the leading coefficient is just 1, we have the following possible (rational) roots to try:
±1, ±2, ±3, ±4, ±6, ±12, ±24
When we substitute one of these numbers for 

Since the function equals zero when 


Now we can factor the function this way:
(x%5E%7B3%7D-5x%5E%7B2%7D-2x+24) $"f(x)=(x+1)(x^{3}$$-5x^{2}$-2x+24)")
We repeat this process, using the Rational Roots Theorem with the second term to find a possible zero. Let's try 
When we factor using synthetic substitution for 
Using our quadratic factoring rules, we can factor completely:
Thus, the zeroes of 
← Didn't Know|Knew It →
Solve for x.

Solve for x.
Tap to reveal answer

- Split up the middle term so that factoring by grouping is possible.
Factors of 10 include:
1 * 10= 10 1 + 10 = 11
2 * 5 =10 2 + 5 = 7
–2 * –5 = 10 –2 + –5 = –7 Good!

- Now factor by grouping, pulling "x" out of the first pair and "-5" out of the second.

- Now pull out the common factor, the "(x-2)," from both terms.

- Set both terms equal to zero to find the possible roots and solve using inverse operations.
x – 5 = 0, x = 5
x – 2 = 0, x = 2
- Split up the middle term so that factoring by grouping is possible.
Factors of 10 include:
1 * 10= 10 1 + 10 = 11
2 * 5 =10 2 + 5 = 7
–2 * –5 = 10 –2 + –5 = –7 Good!
- Now factor by grouping, pulling "x" out of the first pair and "-5" out of the second.
- Now pull out the common factor, the "(x-2)," from both terms.
- Set both terms equal to zero to find the possible roots and solve using inverse operations.
x – 5 = 0, x = 5
x – 2 = 0, x = 2
← Didn't Know|Knew It →
Solve for  :
:

Solve for 
Tap to reveal answer
To solve for  , you need to isolate it to one side of the equation. You can subtract the
, you need to isolate it to one side of the equation. You can subtract the  from the right to the left. Then you can add the 6 from the right to the left:
from the right to the left. Then you can add the 6 from the right to the left:



Next, you can factor out this quadratic equation to solve for  . You need to determine which factors of 8 add up to negative 6:
. You need to determine which factors of 8 add up to negative 6:


Finally, you set each binomial equal to 0 and solve for  :
:

To solve for 

Next, you can factor out this quadratic equation to solve for 
Finally, you set each binomial equal to 0 and solve for 
← Didn't Know|Knew It →
Find the roots of the function:

Find the roots of the function:
Tap to reveal answer
Factor:


Double check by factoring:




Add together: 
Therefore:


Factor:
Double check by factoring:
Add together:
Therefore:
← Didn't Know|Knew It →
Find the roots of  .
.
Find the roots of 
Tap to reveal answer
If we recognize this as an expression with form  , with
, with  and
and  , we can solve this equation by factoring:
, we can solve this equation by factoring:


 and
and 
 and
and 
If we recognize this as an expression with form 




← Didn't Know|Knew It →
Find the zeros of the given polynomial:

Find the zeros of the given polynomial:
Tap to reveal answer
To find the values for  in which the polynomial equals
in which the polynomial equals  , we first want to factor the equation:
, we first want to factor the equation:






To find the values for 

← Didn't Know|Knew It →
If the following is a zero of a polynomial, find another zero.

If the following is a zero of a polynomial, find another zero.
Tap to reveal answer
When finding zeros of a polynomial, you must remember your rules. Without a function this may seem tricky, but remember that non-real solutions come in conjugate pairs. Conjugate pairs differ in the middle sign. Thus, our answer is:

When finding zeros of a polynomial, you must remember your rules. Without a function this may seem tricky, but remember that non-real solutions come in conjugate pairs. Conjugate pairs differ in the middle sign. Thus, our answer is:
← Didn't Know|Knew It →
Tap to reveal answer
← Didn't Know|Knew It →
Tap to reveal answer
← Didn't Know|Knew It →
Tap to reveal answer
← Didn't Know|Knew It →
Tap to reveal answer
← Didn't Know|Knew It →
Tap to reveal answer
← Didn't Know|Knew It →
Tap to reveal answer
← Didn't Know|Knew It →
Tap to reveal answer
← Didn't Know|Knew It →
Tap to reveal answer
← Didn't Know|Knew It →
Tap to reveal answer
← Didn't Know|Knew It →
Tap to reveal answer
← Didn't Know|Knew It →
Tap to reveal answer
← Didn't Know|Knew It →





















