Finding Sides - Math

Card 1 of 220

0

Didn't Know

0

Didn't Know

Knew It

0

1 of 2019 left

Question

What is the length of CB?

Tap to reveal answer

Answer

$\tan X= $\frac{OPPOSITE}{ADJACENT}$$

$\tan C=\frac{AB}{CB}$$

$CB= $\frac{AB}{\tan C}$$

← Didn't Know|Knew It →

Question

If $\theta$ equals and is , how long is ?

Tap to reveal answer

Answer

This problem can be easily solved using trig identities. We are given the hypotenuse and $\theta $(55^{\circ}$)$ . We can then calculate side using the $\sin$ .

$\sin=\frac{opposite}{hypotenuse}$$

Rearrange to solve for .

$\dpi{100} \rightarrow 12.3ft$

If you calculated the side to equal then you utilized the $\cos$ function rather than the $\sin$ .

← Didn't Know|Knew It →

Question

Solve for .

(Figure not drawn to scale).

Tap to reveal answer

Answer

The side-angle-side (SAS) postulate can be used to determine that the triangles are similar. Both triangles share the angle farthest to the right. In the smaller triangle, the upper edge has a length of , and in the larger triangle is has a length of . In the smaller triangle, the bottom edge has a length of , and in the larger triangle is has a length of . We can test for comparison.

$\frac{Upper\ edge_1}{Upper\ edge_2}$=\frac{Lower\ edge_1}{Lower\ edge_2}$

$\frac{8}{16}$=\frac{6}{12}$=\frac{1}{2}$

The statement is true, so the triangles must be similar.

We can use this ratio to solve for the missing side length.

$\frac{Upper\ edge_1}{Upper\ edge_2}$=\frac{Lower\ edge_1}{Lower\ edge_2}$=\frac{x}{Left\ edge_2}$

To simplify, we will only use the lower edge and left edge comparison.

$\small $\frac{6}{12}$=\frac{x}{5}$$

Cross multiply.

$\small 12x=30$

$\small x=\frac{30}{12}$=\frac{5}{2}$=2.5$

← Didn't Know|Knew It →

Question

Solve for .

(Figure not drawn to scale).

Tap to reveal answer

Answer

We can solve using the trigonometric definition of tangent.

$\small tan\Theta =\frac{opp}{adj}$$

We are given the angle and the adjacent side.

$\small $tan(22^o$)=\frac{z}{18}$$

We can find $\small $tan(22^o$)$ with a calculator.

$\small $tan(22^o$)=0.4$

$0.4=\frac{z}{18}$$

$\small 18*0.4=z$

$\small z=7.3$

← Didn't Know|Knew It →

Question

What is the length of CB?

Tap to reveal answer

Answer

$\tan X= $\frac{OPPOSITE}{ADJACENT}$$

$\tan C=\frac{AB}{CB}$$

$CB= $\frac{AB}{\tan C}$$

← Didn't Know|Knew It →

Question

If $\theta$ equals and is , how long is ?

Tap to reveal answer

Answer

This problem can be easily solved using trig identities. We are given the hypotenuse and $\theta $(55^{\circ}$)$ . We can then calculate side using the $\sin$ .

$\sin=\frac{opposite}{hypotenuse}$$

Rearrange to solve for .

$\dpi{100} \rightarrow 12.3ft$

If you calculated the side to equal then you utilized the $\cos$ function rather than the $\sin$ .

← Didn't Know|Knew It →

Question

Solve for .

(Figure not drawn to scale).

Tap to reveal answer

Answer

The side-angle-side (SAS) postulate can be used to determine that the triangles are similar. Both triangles share the angle farthest to the right. In the smaller triangle, the upper edge has a length of , and in the larger triangle is has a length of . In the smaller triangle, the bottom edge has a length of , and in the larger triangle is has a length of . We can test for comparison.

$\frac{Upper\ edge_1}{Upper\ edge_2}$=\frac{Lower\ edge_1}{Lower\ edge_2}$

$\frac{8}{16}$=\frac{6}{12}$=\frac{1}{2}$

The statement is true, so the triangles must be similar.

We can use this ratio to solve for the missing side length.

$\frac{Upper\ edge_1}{Upper\ edge_2}$=\frac{Lower\ edge_1}{Lower\ edge_2}$=\frac{x}{Left\ edge_2}$

To simplify, we will only use the lower edge and left edge comparison.

$\small $\frac{6}{12}$=\frac{x}{5}$$

Cross multiply.

$\small 12x=30$

$\small x=\frac{30}{12}$=\frac{5}{2}$=2.5$

← Didn't Know|Knew It →

Question

Solve for .

(Figure not drawn to scale).

Tap to reveal answer

Answer

We can solve using the trigonometric definition of tangent.

$\small tan\Theta =\frac{opp}{adj}$$

We are given the angle and the adjacent side.

$\small $tan(22^o$)=\frac{z}{18}$$

We can find $\small $tan(22^o$)$ with a calculator.

$\small $tan(22^o$)=0.4$

$0.4=\frac{z}{18}$$

$\small 18*0.4=z$

$\small z=7.3$

← Didn't Know|Knew It →

Question

Note: Figure NOT drawn to scale.

Refer to the above diagram. Evaluate .

Tap to reveal answer

Answer

The altitude perpendicular to the hypotenuse of a right triangle divides that triangle into two smaller triangles similar to each other and the large triangle. Therefore, the sides are in proportion. The hypotenuse of the triangle is equal to

Therefore, we can set up, and solve for in, a proportion statement involving the shorter side and hypotenuse of the large triangle and the larger of the two smaller triangles:

$\frac{N}{12}$ = $\frac{5}{13}$

$$\frac{N}{12}$ \times 12 = $\frac{5}{13}$ \times 12$

$N = $\frac{60}{13}$ = 4$\frac{8}{13}$$

This is not one of the choices.

← Didn't Know|Knew It →

Question

What is the length of the diagonals of trapezoid ? Assume the figure is an isoceles trapezoid.

Tap to reveal answer

Answer

To find the length of the diagonal, we need to use the Pythagorean Theorem. Therefore, we need to sketch the following triangle within trapezoid :

We know that the base of the triangle has length . By subtracting the top of the trapezoid from the bottom of the trapezoid, we get:

Dividing by two, we have the length of each additional side on the bottom of the trapezoid:

$$\frac{6: m}{2}$ = 3: m$

Adding these two values together, we get .

The formula for the length of diagonal uses the Pythagoreon Theorem:

, where is the point between and representing the base of the triangle.

Plugging in our values, we get:

$AC = $\sqrt{97}$: m$

← Didn't Know|Knew It →

Question

Note: Figure NOT drawn to scale.

Refer to the above diagram. Evaluate the length of the hypotenuse of the blue triangle.

Tap to reveal answer

Answer

The inscribed rectangle is a 20 by 20 square. Since opposite sides of the square are parallel, the corresponding angles of the two smaller right triangles are congruent; therefore, the two triangles are similar and, by definition, their sides are in proportion.

The small top triangle has legs 10 and 20. Therefore, the length of its hypotenuse can be determined using the Pythagorean Theorem:

$c = $$\sqrt{10^{2}$$+ $20^{2}$} = $\sqrt{100 + 400}$ = $\sqrt{500}$ = $\sqrt{100}$ \cdot $\sqrt{5}$ = 10 $\sqrt{5}$$

The small top triangle has short leg 10 and hypotenuse $10 $\sqrt{5}$$ . The blue triangle has short leg 20 and unknown hypotenuse , where can be calculated with the proportion statement

$\frac{N}{10\sqrt{5}$} = $\frac{20}{10}$

$\frac{N}{10\sqrt{5}$} \cdot 10$\sqrt{5}$ = $\frac{20}{10}$ \cdot 10$\sqrt{5}$

$N = 20 $\sqrt{5}$$

← Didn't Know|Knew It →

Question

Which of the following describes a triangle with sides one kilometer, 100 meters, and 100 meters?

Tap to reveal answer

Answer

One kilometer is equal to 1,000 meters, so the triangle has sides of length 100, 100, and 1,000. However,

That is, the sum of the least two sidelengths is not greater than the third. This violates the Triangle Inequality, and this triangle cannot exist.

← Didn't Know|Knew It →

Question

Note: figure NOT drawn to scale.

Refer to the triangle in the above diagram.

.

Evaluate .

Tap to reveal answer

Answer

By the Law of Sines,

$$\frac{BC}{\sin $a^{\circ }$$ } = $\frac{AC}{\sin $b^{\circ }$$}$

Substitute and solve for :

$$\frac{BC}{\sin $60^{\circ }$$ } = $\frac{25}{\sin $45^{\circ }$$}$

$\frac{BC}{\sin $60^{\circ }$$ } \cdot \sin $60^{\circ }$ = $\frac{25}{\sin $45^{\circ }$$} \cdot \sin $60^{\circ }$

$BC = $\frac{25\sin $60^{\circ }$$}{\sin $45^{\circ }$}$

$BC= $\frac{25 \cdot \frac{\sqrt{3}$}{2} }{ $\frac{\sqrt{2}$}{2}}$

$BC= $\frac{ \frac{25 \sqrt{3}$}{2} }{ $\frac{\sqrt{2}$}{2}}$

$BC= $\frac{25 \sqrt{3}$}{2} \cdot $\frac{2}{\sqrt{2}$}$

$BC= $\frac{25\sqrt{3}$}{ $\sqrt{2}$ }$

$BC = $\frac{25\sqrt{3}$}{ $\sqrt{2}$ } \cdot $\frac{\sqrt{2}$}{$\sqrt{2}$}$

$BC = $\frac{25\sqrt{6}$}{ 2 }$

← Didn't Know|Knew It →

Question

Note: figure NOT drawn to scale.

Refer to the triangle in the above diagram.

Evaluate . Round to the nearest tenth, if applicable.

Tap to reveal answer

Answer

By the Law of Cosines,

$\left (AC \right $)^{2}$ =\left (AB \right $)^{2}$+ \left (BC \right $)^{2}$ - 2 (AB)(BC) \cos $b^{\circ }$$

Substitute :

$\left (AC \right $)^{2}$ $=15^{2}$$+20^{2}$ - 2 \cdot15 \cdot 20 \cos $45^{\circ }$$

$\left(AC \right $)^{2}$ =225+400 - 600 \cdot $\frac{\sqrt{2}$}{2}$

$\left(AC \right $)^{2}$ \approx 625 -424.26$

$\left(AC \right $)^{2}$ \approx 200.74$

$AC \approx $\sqrt{200.74}$ \approx 14.2$

← Didn't Know|Knew It →

Question

The above figure is a regular pentagon. Evaluate to the nearest tenth.

Tap to reveal answer

Answer

Two sides of the triangle formed measure 4 each; the included angle is one angle of the regular pentagon, which measures

$m = \left [$\frac{180(5-2)}{5}$ \right ] ^{\circ }= $108^{\circ }$$

The length of the third side can be found by applying the Law of Cosines:

where :

$x \approx $\sqrt{41.88}$ \approx 6.5$

← Didn't Know|Knew It →

Question

In triangle $\Delta GHJ$ , $m\angle G = $50^{\circ }$$ and $m \angle H = $65^{\circ }$$ .

Which of the following statements is true about the lengths of the sides of $\Delta GHJ$ ?

Tap to reveal answer

Answer

In a triangle, the shortest side is opposite the angle of least measure; the longest side is opposite the angle of greatest measure. Therefore, if we order the angles, we can order their opposite sides similarly.

Since the measures of the three interior angles of a triangle must total ,

$m \angle J + m \angle G + m \angle H = $180^{\circ }$$

$m \angle J + 50 ^{\circ }+ $65^{\circ }$ = $180^{\circ }$$

$m \angle J + $115^{\circ }$ = $180^{\circ }$$

$m \angle J $=65^{\circ }$$

$\angle G$ has the least degree measure, so its opposite side, $\overline{HJ}$ , is the shortest. $\angle H \cong \angle J$ , so by the Isosceles Triangle Theorem, their opposite sides $\overline{GJ}$ and $\overline{GH}$ are congruent. Therefore, the correct choice is

.

← Didn't Know|Knew It →

Question

Assume quadrilateral $\small ABCD$ is a rhombus. The perimeter of $\small ABCD$ is , and the length of one of its diagonals is $\small 12$ . What is the area of $\small ABCD$ ?

Tap to reveal answer

Answer

To solve for the area of the rhombus $\small ABCD$ , we must use the equation $\small A=\frac{pq}{2}$$ , where $\small p$ and $\small q$ are the diagonals of the rhombus. Since the perimeter of the rhombus is $\small 40$ , and by definition all 4 sides of a rhombus have the same length, we know that the length of each side is $\small 10$ . We can find the length of the other diagonal if we recognize that the two diagonals combined with a side edge form a right triangle. The length of the hypotenuse is $\small 10$ , and each leg of the triangle is equal to one-half of each diagonal. We can therefore set up an equation involving Pythagorean's Theorem as follows:

$\small $10^2$$=x^2$$+6^2$$ , where $\small x$ is equal to one-half the length of the unknown diagonal.

We can therefore solve for $\small x$ as follows:

$\small $x^2$$=10^2$$-6^2$=100-36=64$

$\small x$ is therefore equal to 8, and our other diagonal is 16. We can now use both diagonals to solve for the area of the rhombus:

$\small A=\frac{(16)(12)}{2}$=\frac{192}{2}$=96$

The area of rhombus $\small ABCD$ is therefore equal to $\small 96$

← Didn't Know|Knew It →

Question

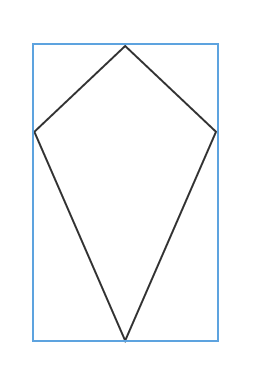
The area of the rectangle is , what is the area of the kite?

Tap to reveal answer

Answer

The area of a kite is half the product of the diagonals.

$A=\frac{p \cdot q}{2}$$

The diagonals of the kite are the height and width of the rectangle it is superimposed in, and we know that because the area of a rectangle is base times height.

Therefore our equation becomes:

$A=\frac{l \cdot w}{2}$$ .

We also know the area of the rectangle is $A=l \cdot w=80$ . Substituting this value in we get the following:

$A=\frac{l \cdot w}{2}$=\frac{80}{2}$=40$

Thus,, the area of the kite is .

← Didn't Know|Knew It →

Question

is a rhombus with side length . Diagonal $\overline{BD}$ has a length of . Find the length of diagonal $\overline{AC}$ .

Tap to reveal answer

Answer

A rhombus is a quadrilateral with four sides of equal length. Rhombuses have diagonals that bisect each other at right angles.

Thus, we can consider the right triangle to find the length of diagonal $\overline{AC}$ . From the problem, we are given that the sides are and $$\overline{BD}$ = 12:cm$ . Because the diagonals bisect each other, we know:

$$\overline{AD}$ = 10:cm$

$$\overline{ED}$ = 6:cm$

Using the Pythagorean Theorem,

$$\overline{AE}$ = 8:cm$

$$\overline{AC}$ = 16:cm$

← Didn't Know|Knew It →

Question

is a rhombus. $$\overline{AB}$ = 17:cm$ $$\overline{AB}$ = 17$ and $$\overline{AC}$ = 30:cm$ . Find $\overline{BD}$ .

Tap to reveal answer

Answer

A rhombus is a quadrilateral with four sides of equal length. Rhombuses have diagonals that bisect each other at right angles.

Thus, we can consider the right triangle to find the length of diagonal $\overline{BD}$ . From the problem, we are given that the sides are and $$\overline{AC}$ = 30:cm$ . Because the diagonals bisect each other, we know:

$$\overline{AD}$ = 17:cm$

$$\overline{AE}$ = 15:cm$

Using the Pythagorean Theorem,

$$\overline{ED}$ = 8:cm$

$$\overline{BD}$ = 16:cm$

← Didn't Know|Knew It →

0

Knew It