Equilateral Triangles - Math
Card 0 of 504
What is the height of an equilateral triangle with a side length of 8 in?
What is the height of an equilateral triangle with a side length of 8 in?
Tap to see back →
An equilateral triangle has three congruent sides, and is also an equiangular triangle with three congruent angles that each meansure 60 degrees.
To find the height we divide the triangle into two special 30 - 60 - 90 right triangles by drawing a line from one corner to the center of the opposite side. This segment will be the height, and will be opposite from one of the 60 degree angles and adjacent to a 30 degree angle. The special right triangle gives side ratios of 
, 
, and 
. The hypoteneuse, the side opposite the 90 degree angle, is the full length of one side of the triangle and is equal to 
. Using this information, we can find the lengths of each side fo the special triangle.
The side with length 
will be the height (opposite the 60 degree angle). The height is 
inches.
An equilateral triangle has three congruent sides, and is also an equiangular triangle with three congruent angles that each meansure 60 degrees.
To find the height we divide the triangle into two special 30 - 60 - 90 right triangles by drawing a line from one corner to the center of the opposite side. This segment will be the height, and will be opposite from one of the 60 degree angles and adjacent to a 30 degree angle. The special right triangle gives side ratios of
The side with length
ΔABC is an equilateral triangle with side of length 8.
Find the height (to the nearest tenth).
ΔABC is an equilateral triangle with side of length 8.
Find the height (to the nearest tenth).
Tap to see back →
Equilateral triangles have sides of equal length, with angles of 60°. To find the height, we can draw an altitude to one of the sides in order to split the triangle into two equal 30-60-90 triangles.
Now, the side of the original equilateral triangle (lets call it "a") is the hypotenuse of the 30-60-90 triangle. Because the 30-60-90 triange is a special triangle, we know that the sides are x, x
, and 2x, respectively.
Thus, a = 2x and x = a/2.
Height of the equilateral triangle = 
Equilateral triangles have sides of equal length, with angles of 60°. To find the height, we can draw an altitude to one of the sides in order to split the triangle into two equal 30-60-90 triangles.
Now, the side of the original equilateral triangle (lets call it "a") is the hypotenuse of the 30-60-90 triangle. Because the 30-60-90 triange is a special triangle, we know that the sides are x, x
Thus, a = 2x and x = a/2.
Height of the equilateral triangle =
ΔABC is an equilateral triangle with side 12.
Find the height of ΔABC (to the nearest tenth).
ΔABC is an equilateral triangle with side 12.
Find the height of ΔABC (to the nearest tenth).
Tap to see back →
Equilateral triangles have sides of all equal length and angles of 60°. To find the height, we can draw an altitude to one of the sides in order to split the triangle into two equal 30-60-90 triangles.
Now, the side of the original equilateral triangle (lets call it "a") is the hypotenuse of the 30-60-90 triangle. Because the 30-60-90 triange is a special triangle, we know that the sides are x, x
, and 2x, respectively.
Thus, a = 2x and x = a/2.
Height of the equilateral triangle = 
Equilateral triangles have sides of all equal length and angles of 60°. To find the height, we can draw an altitude to one of the sides in order to split the triangle into two equal 30-60-90 triangles.
Now, the side of the original equilateral triangle (lets call it "a") is the hypotenuse of the 30-60-90 triangle. Because the 30-60-90 triange is a special triangle, we know that the sides are x, x
Thus, a = 2x and x = a/2.
Height of the equilateral triangle =
Find the height of an equilateral triangle with a side length of 
. Round your answer to the nearest tenth.
Find the height of an equilateral triangle with a side length of
Tap to see back →
An equilateral triangle has three equal sides, as can be deduced from its name. This also means that as a result, the triangle is also equiangular. That is, all its interior angles are the same. Because the sum of internal angles of a triangle is 
, that means that each interior angle is 
.
The height (the dotted line in the diagram) is the length that bisects the apical angle while bisecting the base of the triangle. Drawing the dotted line splits the equilateral triangle into two congruent right triangles. Because they're the same, we only need to consider one of the two smaller triangles to obtain our answer. Keeping in mind that the base of the equilateral triangle has been bisected, this means that the base of the right triangle has the length of 
. With a base of 
and a hypotenuse of 
, we can easily solve for the height (the third side) with the Pythagorean Theorem.
This problem can also be solved using trigonometric functions or even revisiting 30-60-90 triangle rules.
Using the Pythagorean Theorem,
Therefore, the height of the equilateral triangle is 
.
An equilateral triangle has three equal sides, as can be deduced from its name. This also means that as a result, the triangle is also equiangular. That is, all its interior angles are the same. Because the sum of internal angles of a triangle is
The height (the dotted line in the diagram) is the length that bisects the apical angle while bisecting the base of the triangle. Drawing the dotted line splits the equilateral triangle into two congruent right triangles. Because they're the same, we only need to consider one of the two smaller triangles to obtain our answer. Keeping in mind that the base of the equilateral triangle has been bisected, this means that the base of the right triangle has the length of
This problem can also be solved using trigonometric functions or even revisiting 30-60-90 triangle rules.
Using the Pythagorean Theorem,
Therefore, the height of the equilateral triangle is
What is the height of a triangle with side lengths 4, 4, 4?
What is the height of a triangle with side lengths 4, 4, 4?
Tap to see back →
To solve, it's easiest to first visualize the height's relationship with the rest of the triangle's sides:
The height is one of the legs of a right triangle. The hypotenuse is 4, and the other leg is 2, or half of the base side, 4. To determine the height, use Pythagorean Theorem:
subtract 4 from both sides
take the square root of both sides
To solve, it's easiest to first visualize the height's relationship with the rest of the triangle's sides:
The height is one of the legs of a right triangle. The hypotenuse is 4, and the other leg is 2, or half of the base side, 4. To determine the height, use Pythagorean Theorem:
If an equilateral triangle has a length of 
for all sides, what would be the heigh of the triangle? Round to the nearest tenth.
If an equilateral triangle has a length of
Tap to see back →
The following formula can be used to determine the height of an equilateral triangle when we are given the length of the sides:
The following formula can be used to determine the height of an equilateral triangle when we are given the length of the sides:
The equilateral triangle shown below has a side length of 
. Given this information, solve for the height of the triangle.
The equilateral triangle shown below has a side length of
Tap to see back →
To solve for the height of an equilateral triangle, we can divide the triangle into two right triangles. In the below image, the bisecting line represents the height, and we can solve for height by applying the Pythagorean Theorem:
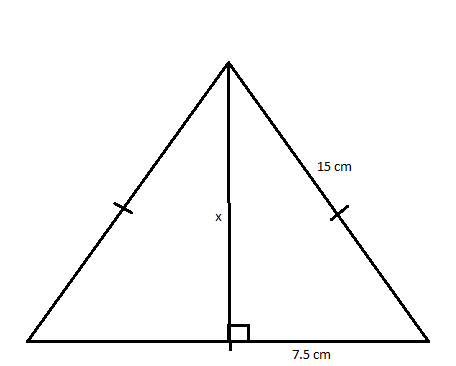
To solve for the height of an equilateral triangle, we can divide the triangle into two right triangles. In the below image, the bisecting line represents the height, and we can solve for height by applying the Pythagorean Theorem:
You are given that the perimeter of an equilateral triangle is 
meters. What is the length of one side of that triangle?
You are given that the perimeter of an equilateral triangle is
Tap to see back →
By definition, an equilateral triangle has three congruent sides. The perimeter is the sum of those sides. Thus, to find the length of just one of those sides, we can divide the perimeter of the triangle by three.
divided by 
is 
meters, which is our answer.
By definition, an equilateral triangle has three congruent sides. The perimeter is the sum of those sides. Thus, to find the length of just one of those sides, we can divide the perimeter of the triangle by three.
The area of an equilateral triangle is 
, what is the length of each side?
The area of an equilateral triangle is
Tap to see back →
An equilateral triangle can be broken down into 2 30-60-90 right triangles (see image). The length of a side (the base) is 2x while the length of the height is 
. The area of a triangle can be calculated using the following equation:
Therefore, if 
equals the length of a side:
A length of the side equals 2x:
An equilateral triangle can be broken down into 2 30-60-90 right triangles (see image). The length of a side (the base) is 2x while the length of the height is
Therefore, if
A length of the side equals 2x:
What is the area of this triangle if 
?
What is the area of this triangle if
Tap to see back →
We know the formula for the area of an equilateral triangle is:
if 
is the side of the triangle.
So, since we are told that 
, we can substitute in 
for 
and solve for the area of the triangle:
We know the formula for the area of an equilateral triangle is:
if
So, since we are told that
Find 
if the perimeter of this triangle is 
.
Find
Tap to see back →
This triangle is equilateral; we can tell because each of its sides are the same length, 
. To find the length of one side, we need to divide the perimeter by 
:
This triangle is equilateral; we can tell because each of its sides are the same length,
What is side 
if the perimeter of this triangle is 
?
What is side
Tap to see back →
Since each of this triangle's sides is equal in length, it is equilateral. To find the length of one side of an equilateral triangle, we need to divide the perimeter by 
.
Since each of this triangle's sides is equal in length, it is equilateral. To find the length of one side of an equilateral triangle, we need to divide the perimeter by
The height of the triangle is 
feet.
What is the length of the base of the triangle to the nearest tenth?
The height of the triangle is
What is the length of the base of the triangle to the nearest tenth?
Tap to see back →
Since it is an equilateral triangle, the line that represents the height bisects it into a 30-60-90 triangle.
Here you may use 
and solve for hypotenuse to find one of the sides of the triangle.
Use the definition of an equilateral triangle to know that the answer of the hypotenuse also applies to the base of the triangle.
Therefore,
Since it is an equilateral triangle, the line that represents the height bisects it into a 30-60-90 triangle.
Here you may use
Use the definition of an equilateral triangle to know that the answer of the hypotenuse also applies to the base of the triangle.
Therefore,
The height of an equilateral triangle is 5. How long are its sides?
The height of an equilateral triangle is 5. How long are its sides?
Tap to see back →
The height of an equilateral triangle, shown by the dotted line, is also one of the legs of a right triangle:
The hypotenuse is x, the length of each side in this equilateral triangle, and then the other leg is half of that, 0.5x.
To solve for x, use Pythagorean Theorem:
square the terms on the left
combine like terms by subtracting 0.25 x squared from both sides
divide both sides by 0.75
take the square root of both sides
The height of an equilateral triangle, shown by the dotted line, is also one of the legs of a right triangle:
The hypotenuse is x, the length of each side in this equilateral triangle, and then the other leg is half of that, 0.5x.
To solve for x, use Pythagorean Theorem:
An equilateral triangle is placed on top of a square as shown by the figure below.
Find the perimeter of the shape.
An equilateral triangle is placed on top of a square as shown by the figure below.
Find the perimeter of the shape.
Tap to see back →
Recall that the perimeter is the sum of all the exterior sides of a shape. The sides that add up to the perimeter are highlighted in red.
Since the equilateral triangle shares a side with the square, each of the five sides that are outlined have the same length.
Recall that the height of an equilateral triangle splits the triangle into 
congruent 
triangles.
We can then use the height to find the length of the side of the triangle.
Recall that a 
triangle has sides that are in ratios of 
. The smallest side in the given figure is the base, the second longest side is the height, and the longest side is the side of the triangle itself.
Thus, we can use the ratio and the length of the height to set up the following equation:
Plug in the given height to find the length of the side.
Now, since the perimeter of the shape consists of 
of these sides, we can use the following equation to find the perimeter.
Recall that the perimeter is the sum of all the exterior sides of a shape. The sides that add up to the perimeter are highlighted in red.
Since the equilateral triangle shares a side with the square, each of the five sides that are outlined have the same length.
Recall that the height of an equilateral triangle splits the triangle into
We can then use the height to find the length of the side of the triangle.
Recall that a
Thus, we can use the ratio and the length of the height to set up the following equation:
Plug in the given height to find the length of the side.
Now, since the perimeter of the shape consists of
An equilateral triangle is placed on top of a square as shown by the figure below.
Find the perimeter of the shape.
An equilateral triangle is placed on top of a square as shown by the figure below.
Find the perimeter of the shape.
Tap to see back →
Recall that the perimeter is the sum of all the exterior sides of a shape. The sides that add up to the perimeter are highlighted in red.
Since the equilateral triangle shares a side with the square, each of the five sides that are outlined have the same length.
Recall that the height of an equilateral triangle splits the triangle into 
congruent 
triangles.
We can then use the height to find the length of the side of the triangle.
Recall that a 
triangle has sides that are in ratios of 
. The smallest side in the given figure is the base, the second longest side is the height, and the longest side is the side of the triangle itself.
Thus, we can use the ratio and the length of the height to set up the following equation:
Plug in the given height to find the length of the side.
Now, since the perimeter of the shape consists of 
of these sides, we can use the following equation to find the perimeter.
Recall that the perimeter is the sum of all the exterior sides of a shape. The sides that add up to the perimeter are highlighted in red.
Since the equilateral triangle shares a side with the square, each of the five sides that are outlined have the same length.
Recall that the height of an equilateral triangle splits the triangle into
We can then use the height to find the length of the side of the triangle.
Recall that a
Thus, we can use the ratio and the length of the height to set up the following equation:
Plug in the given height to find the length of the side.
Now, since the perimeter of the shape consists of
An equilateral triangle is placed on top of a square, as shown by the figure below.
Find the perimeter of the shape.
An equilateral triangle is placed on top of a square, as shown by the figure below.
Find the perimeter of the shape.
Tap to see back →
Recall that the perimeter is the sum of all the exterior sides of a shape. The sides that add up to the perimeter are highlighted in red.
Since the equilateral triangle shares a side with the square, each of the five sides that are outlined have the same length.
Recall that the height of an equilateral triangle splits the triangle into 
congruent 
triangles.
We can then use the height to find the length of the side of the triangle.
Recall that a 
triangle has sides that are in ratios of 
. The smallest side in the given figure is the base, the second longest side is the height, and the longest side is the side of the triangle itself.
Thus, we can use the ratio and the length of the height to set up the following equation:
Plug in the given height to find the length of the side.
Now, since the perimeter of the shape consists of 
of these sides, we can use the following equation to find the perimeter.
Recall that the perimeter is the sum of all the exterior sides of a shape. The sides that add up to the perimeter are highlighted in red.
Since the equilateral triangle shares a side with the square, each of the five sides that are outlined have the same length.
Recall that the height of an equilateral triangle splits the triangle into
We can then use the height to find the length of the side of the triangle.
Recall that a
Thus, we can use the ratio and the length of the height to set up the following equation:
Plug in the given height to find the length of the side.
Now, since the perimeter of the shape consists of
An equilateral triangle is placed on top of a square as shown by the figure below.
Find the perimeter of the shape.
An equilateral triangle is placed on top of a square as shown by the figure below.
Find the perimeter of the shape.
Tap to see back →
Recall that the perimeter is the sum of all the exterior sides of a shape. The sides that add up to the perimeter are highlighted in red.
Since the equilateral triangle shares a side with the square, each of the five sides that are outlined have the same length.
Recall that the height of an equilateral triangle splits the triangle into 
congruent 
triangles.
We can then use the height to find the length of the side of the triangle.
Recall that a 
triangle has sides that are in ratios of 
. The smallest side in the given figure is the base, the second longest side is the height, and the longest side is the side of the triangle itself.
Thus, we can use the ratio and the length of the height to set up the following equation:
Plug in the given height to find the length of the side.
Now, since the perimeter of the shape consists of 
of these sides, we can use the following equation to find the perimeter.
Recall that the perimeter is the sum of all the exterior sides of a shape. The sides that add up to the perimeter are highlighted in red.
Since the equilateral triangle shares a side with the square, each of the five sides that are outlined have the same length.
Recall that the height of an equilateral triangle splits the triangle into
We can then use the height to find the length of the side of the triangle.
Recall that a
Thus, we can use the ratio and the length of the height to set up the following equation:
Plug in the given height to find the length of the side.
Now, since the perimeter of the shape consists of
An equilateral triangle is placed on top of a square as shown by the figure below.
Find the perimeter of the shape.
An equilateral triangle is placed on top of a square as shown by the figure below.
Find the perimeter of the shape.
Tap to see back →
Recall that the perimeter is the sum of all the exterior sides of a shape. The sides that add up to the perimeter are highlighted in red.
Since the equilateral triangle shares a side with the square, each of the five sides that are outlined have the same length.
Recall that the height of an equilateral triangle splits the triangle into 
congruent 
triangles.
We can then use the height to find the length of the side of the triangle.
Recall that a 
triangle has sides that are in ratios of 
. The smallest side in the given figure is the base, the second longest side is the height, and the longest side is the side of the triangle itself.
Thus, we can use the ratio and the length of the height to set up the following equation:
Plug in the given height to find the length of the side.
Now, since the perimeter of the shape consists of 
of these sides, we can use the following equation to find the perimeter.
Recall that the perimeter is the sum of all the exterior sides of a shape. The sides that add up to the perimeter are highlighted in red.
Since the equilateral triangle shares a side with the square, each of the five sides that are outlined have the same length.
Recall that the height of an equilateral triangle splits the triangle into
We can then use the height to find the length of the side of the triangle.
Recall that a
Thus, we can use the ratio and the length of the height to set up the following equation:
Plug in the given height to find the length of the side.
Now, since the perimeter of the shape consists of
An equilateral triangle is placed on a square as shown by the figure below.
Find the perimeter of the shape.
An equilateral triangle is placed on a square as shown by the figure below.
Find the perimeter of the shape.
Tap to see back →
Recall that the perimeter is the sum of all the exterior sides of a shape. The sides that add up to the perimeter are highlighted in red.
Since the equilateral triangle shares a side with the square, each of the five sides that are outlined have the same length.
Recall that the height of an equilateral triangle splits the triangle into 
congruent 
triangles.
We can then use the height to find the length of the side of the triangle.
Recall that a 
triangle has sides that are in ratios of 
. The smallest side in the given figure is the base, the second longest side is the height, and the longest side is the side of the triangle itself.
Thus, we can use the ratio and the length of the height to set up the following equation:
Plug in the given height to find the length of the side.
Now, since the perimeter of the shape consists of 
of these sides, we can use the following equation to find the perimeter.
Recall that the perimeter is the sum of all the exterior sides of a shape. The sides that add up to the perimeter are highlighted in red.
Since the equilateral triangle shares a side with the square, each of the five sides that are outlined have the same length.
Recall that the height of an equilateral triangle splits the triangle into
We can then use the height to find the length of the side of the triangle.
Recall that a
Thus, we can use the ratio and the length of the height to set up the following equation:
Plug in the given height to find the length of the side.
Now, since the perimeter of the shape consists of