Applying Taylor Series - Math
Card 1 of 4
Give the  term of the Maclaurin series expansion of the function
term of the Maclaurin series expansion of the function  .
.
Give the 

Tap to reveal answer
The  term of a Maclaurin series expansion has coefficient
term of a Maclaurin series expansion has coefficient
 .
.
We can find  by differentiating twice in succession:
by differentiating twice in succession:




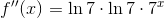


The coefficient we want is
 ,
,
so the corresponding term is  .
.
The 

We can find 
The coefficient we want is

so the corresponding term is 
← Didn't Know|Knew It →
Give the  term of the Maclaurin series expansion of the function
term of the Maclaurin series expansion of the function  .
.
Give the 

Tap to reveal answer
The  term of a Maclaurin series expansion has coefficient
term of a Maclaurin series expansion has coefficient
 .
.
We can find  by differentiating twice in succession:
by differentiating twice in succession:




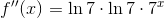


The coefficient we want is
 ,
,
so the corresponding term is  .
.
The 

We can find 
The coefficient we want is

so the corresponding term is 
← Didn't Know|Knew It →
Give the  term of the Maclaurin series expansion of the function
term of the Maclaurin series expansion of the function  .
.
Give the 

Tap to reveal answer
The  term of a Maclaurin series expansion has coefficient
term of a Maclaurin series expansion has coefficient
 .
.
We can find  by differentiating twice in succession:
by differentiating twice in succession:




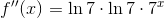


The coefficient we want is
 ,
,
so the corresponding term is  .
.
The 

We can find 
The coefficient we want is

so the corresponding term is 
← Didn't Know|Knew It →
Give the  term of the Maclaurin series expansion of the function
term of the Maclaurin series expansion of the function  .
.
Give the 

Tap to reveal answer
The  term of a Maclaurin series expansion has coefficient
term of a Maclaurin series expansion has coefficient
 .
.
We can find  by differentiating twice in succession:
by differentiating twice in succession:




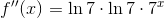


The coefficient we want is
 ,
,
so the corresponding term is  .
.
The 

We can find 
The coefficient we want is

so the corresponding term is 
← Didn't Know|Knew It →