Functions and Graphs - Math
Card 1 of 608
List the transformations that have been enacted upon the following equation:
List the transformations that have been enacted upon the following equation:
Tap to reveal answer
Since the equation given in the question is based off of the parent function 
, we can write the general form for transformations like this:
determines the vertical stretch or compression factor.
- If
is greater than 1, the function has been vertically stretched (expanded) by a factor of 
.
- If
is between 0 and 1, the function has been vertically compressed by a factor of 
.
In this case, 
is 4, so the function has been vertically stretched by a factor of 4.
determines the horizontal stretch or compression factor.
- If
is greater than 1, the function has been horizontally compressed by a factor of 
.
- If
is between 0 and 1, the function has been horizontally stretched (expanded) by a factor of 
.
In this case, 
is 6, so the function has been horizontally compressed by a factor of 6. (Remember that horizontal stretch and compression are opposite of vertical stretch and compression!)
determines the horizontal translation.
- If
is positive, the function was translated 
units right.
- If
is negative, the function was translated 
units left.
In this case, 
is 3, so the function was translated 3 units right.
determines the vertical translation.
- If
is positive, the function was translated 
units up.
- If
is negative, the function was translated 
units down.
In this case, 
is -7, so the function was translated 7 units down.
Since the equation given in the question is based off of the parent function
- If
- If
In this case,
- If
- If
In this case,
- If
- If
In this case,
- If
- If
In this case,
← Didn't Know|Knew It →
Based on the figure below, which line depicts a quadratic function?
Based on the figure below, which line depicts a quadratic function?
Tap to reveal answer
A parabola is one example of a quadratic function, regardless of whether it points upwards or downwards.
The red line represents a quadratic function and will have a formula similar to 
.
The blue line represents a linear function and will have a formula similar to 
.
The green line represents an exponential function and will have a formula similar to 
.
The purple line represents an absolute value function and will have a formula similar to 
.
A parabola is one example of a quadratic function, regardless of whether it points upwards or downwards.
The red line represents a quadratic function and will have a formula similar to
The blue line represents a linear function and will have a formula similar to
The green line represents an exponential function and will have a formula similar to
The purple line represents an absolute value function and will have a formula similar to
← Didn't Know|Knew It →
Which of the following functions represents a parabola?
Which of the following functions represents a parabola?
Tap to reveal answer
A parabola is a curve that can be represented by a quadratic equation. The only quadratic here is represented by the function 
, while the others represent straight lines, circles, and other curves.
A parabola is a curve that can be represented by a quadratic equation. The only quadratic here is represented by the function
← Didn't Know|Knew It →
Write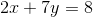 
in slope-intercept form.
Write
Tap to reveal answer
Slope-intercept form is 
.
Slope-intercept form is
← Didn't Know|Knew It →
Find the 
-intercepts for the circle given by the equation:
Find the
Tap to reveal answer
To find the 
-intercepts (where the graph crosses the 
-axis), we must set 
. This gives us the equation:
Because the left side of the equation is squared, it will always give us a positive answer. Thus if we want to take the root of both sides, we must account for this by setting up two scenarios, one where the value inside of the parentheses is positive and one where it is negative. This gives us the equations:
and 
We can then solve these two equations to obtain 
.
To find the
Because the left side of the equation is squared, it will always give us a positive answer. Thus if we want to take the root of both sides, we must account for this by setting up two scenarios, one where the value inside of the parentheses is positive and one where it is negative. This gives us the equations:
We can then solve these two equations to obtain
← Didn't Know|Knew It →
Find the 
-intercepts for the circle given by the equation:
Find the
Tap to reveal answer
To find the 
-intercepts (where the graph crosses the 
-axis), we must set 
. This gives us the equation:
Because the left side of the equation is squared, it will always give us a positive answer. Thus if we want to take the root of both sides, we must account for this by setting up two scenarios, one where the value inside of the parentheses is positive and one where it is negative. This gives us the equations:
and 
We can then solve these two equations to obtain
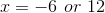
To find the
Because the left side of the equation is squared, it will always give us a positive answer. Thus if we want to take the root of both sides, we must account for this by setting up two scenarios, one where the value inside of the parentheses is positive and one where it is negative. This gives us the equations:
We can then solve these two equations to obtain
← Didn't Know|Knew It →
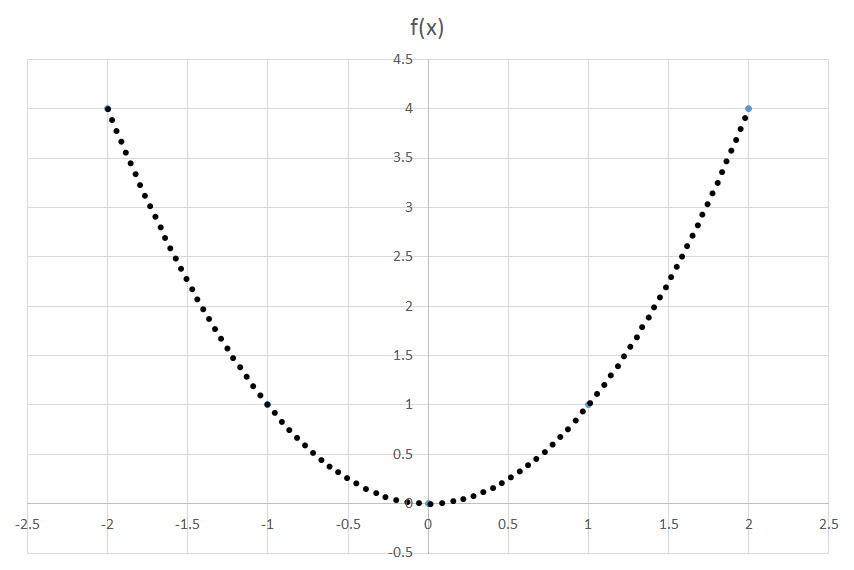
If the function 
is depicted here, which answer choice graphs 
?
If the function
Tap to reveal answer
The function 
shifts a function f(x) 
units to the left. Conversely, 
shifts a function f(x) 
units to the right. In this question, we are translating the graph two units to the left.
To translate along the y-axis, we use the function 
or 
.
The function
To translate along the y-axis, we use the function
← Didn't Know|Knew It →
Let 
. What is 
?
Let
Tap to reveal answer
We are asked to find 
, which is the inverse of a function.
In order to find the inverse, the first thing we want to do is replace f(x) with y. (This usually makes it easier to separate x from its function.).
Next, we will swap x and y.
Then, we will solve for y. The expression that we determine will be equal to 
.
Subtract 5 from both sides.
Multiply both sides by -1.
We need to raise both sides of the equation to the 1/3 power in order to remove the exponent on the right side.
We will apply the general property of exponents which states that 
.
Laslty, we will subtract one from both sides.
The expression equal to y is equal to the inverse of the original function f(x). Thus, we can replace y with 
.
The answer is 
.
We are asked to find
In order to find the inverse, the first thing we want to do is replace f(x) with y. (This usually makes it easier to separate x from its function.).
Next, we will swap x and y.
Then, we will solve for y. The expression that we determine will be equal to
Subtract 5 from both sides.
Multiply both sides by -1.
We need to raise both sides of the equation to the 1/3 power in order to remove the exponent on the right side.
We will apply the general property of exponents which states that
Laslty, we will subtract one from both sides.
The expression equal to y is equal to the inverse of the original function f(x). Thus, we can replace y with
The answer is
← Didn't Know|Knew It →
What is the inverse of 
?
What is the inverse of
Tap to reveal answer
The inverse of 
requires us to interchange 
and 
and then solve for 
.
Then solve for 
:
The inverse of
Then solve for
← Didn't Know|Knew It →
If 
, what is 
?
If
Tap to reveal answer
To find the inverse of a function, exchange the 
and 
variables and then solve for 
.
To find the inverse of a function, exchange the
← Didn't Know|Knew It →
Find the -intercepts for the circle given by the equation:
Find the
Tap to reveal answer
To find the -intercepts (where the graph crosses the -axis), we must set . This gives us the equation:
Because the left side of the equation is squared, it will always give us a positive answer. Thus if we want to take the root of both sides, we must account for this by setting up two scenarios, one where the value inside of the parentheses is positive and one where it is negative. This gives us the equations:
and
We can then solve these two equations to obtain .
To find the
Because the left side of the equation is squared, it will always give us a positive answer. Thus if we want to take the root of both sides, we must account for this by setting up two scenarios, one where the value inside of the parentheses is positive and one where it is negative. This gives us the equations:
We can then solve these two equations to obtain
← Didn't Know|Knew It →
Find the -intercepts for the circle given by the equation:
Find the
Tap to reveal answer
To find the -intercepts (where the graph crosses the -axis), we must set . This gives us the equation:
Because the left side of the equation is squared, it will always give us a positive answer. Thus if we want to take the root of both sides, we must account for this by setting up two scenarios, one where the value inside of the parentheses is positive and one where it is negative. This gives us the equations:
and
We can then solve these two equations to obtain
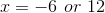
To find the
Because the left side of the equation is squared, it will always give us a positive answer. Thus if we want to take the root of both sides, we must account for this by setting up two scenarios, one where the value inside of the parentheses is positive and one where it is negative. This gives us the equations:
We can then solve these two equations to obtain
← Didn't Know|Knew It →
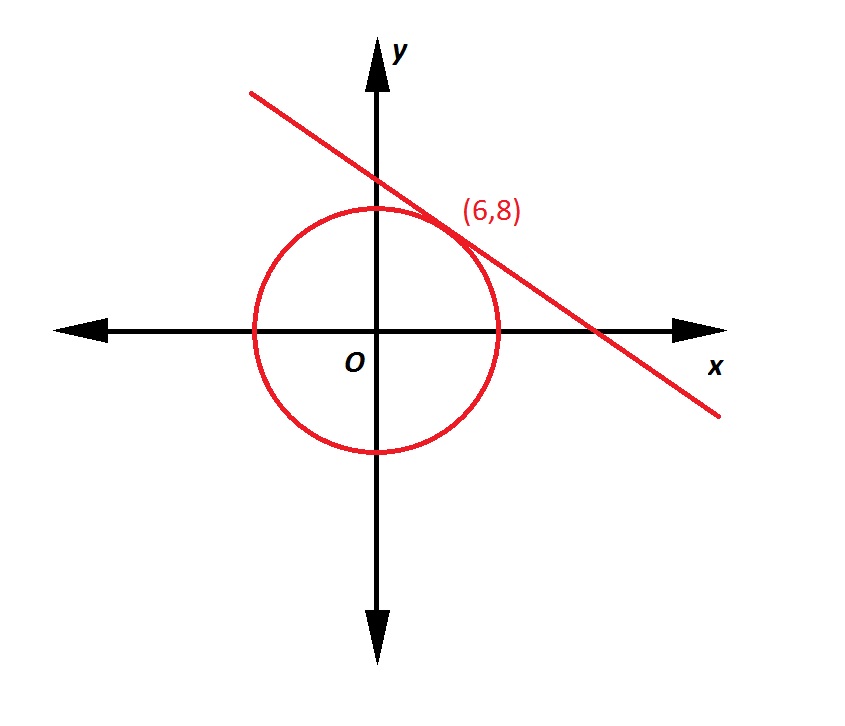
Note: Figure NOT drawn to scale.
Refer to the above figure. The circle has its center at the origin; the line is tangent to the circle at the point indicated. What is the equation of the line in slope-intercept form?
Note: Figure NOT drawn to scale.
Refer to the above figure. The circle has its center at the origin; the line is tangent to the circle at the point indicated. What is the equation of the line in slope-intercept form?
Tap to reveal answer
A line tangent to a circle at a given point is perpendicular to the radius from the center to that point. That radius, which has endpoints 
, has slope
.
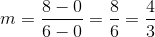The line, being perpendicular to this radius, will have slope equal to the opposite of the reciprocal of that of the radius. This slope will be 
. Since it includes point 
, we can use the point-slope form of the line to find its equation:
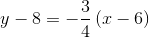
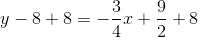
A line tangent to a circle at a given point is perpendicular to the radius from the center to that point. That radius, which has endpoints
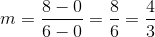
The line, being perpendicular to this radius, will have slope equal to the opposite of the reciprocal of that of the radius. This slope will be
← Didn't Know|Knew It →
What transformations have been enacted upon 
when compared to its parent function, 
?
What transformations have been enacted upon
Tap to reveal answer
First, we need to get this function into a more standard form.
Now we can see that while the function is being horizontally compressed by a factor of 2, it's being translated 3 units to the right, not 6. (It's also being vertically stretched by a factor of 4, of course.)
First, we need to get this function into a more standard form.
Now we can see that while the function is being horizontally compressed by a factor of 2, it's being translated 3 units to the right, not 6. (It's also being vertically stretched by a factor of 4, of course.)
← Didn't Know|Knew It →
If 
and 
, what is 
?
If
Tap to reveal answer
In this problem, the 
in the 
equation becomes 
--> 
.
This simplifies to 
, or
.
In this problem, the
This simplifies to
← Didn't Know|Knew It →
Define 
and 
.
Find 
.
Define
Find
Tap to reveal answer
By definition, 
, so
By definition,
← Didn't Know|Knew It →
Define 
and 
.
Find 
.
Define
Find
Tap to reveal answer
By definition, 
, so
By definition,
← Didn't Know|Knew It →
Write the transformation of the given function moved five units to the left:
Write the transformation of the given function moved five units to the left:
Tap to reveal answer
To transform the function horizontally, we must make an addition or subtraction to the input, x. Because we are asked to move the function to the left, we must add the number of units we are moving. This is the opposite of what one would expect, but if we are inputting values that are to the left of the original, they are less than what would have originally been. So, to counterbalance this, we add the units of the transformation.
For our function being transformed five units to the left, we get
To transform the function horizontally, we must make an addition or subtraction to the input, x. Because we are asked to move the function to the left, we must add the number of units we are moving. This is the opposite of what one would expect, but if we are inputting values that are to the left of the original, they are less than what would have originally been. So, to counterbalance this, we add the units of the transformation.
For our function being transformed five units to the left, we get
← Didn't Know|Knew It →
Transform the function by moving it two units up, and five units to the left:
Transform the function by moving it two units up, and five units to the left:
Tap to reveal answer
To transform a function we use the following formula,
where h represents the horizontal shift and v represents the vertical shift.
In this particular case we want to shift to the left five units,
and vertically up two units,
.
Therefore, the transformed function becomes,
.
To transform a function we use the following formula,
where h represents the horizontal shift and v represents the vertical shift.
In this particular case we want to shift to the left five units,
and vertically up two units,
Therefore, the transformed function becomes,
← Didn't Know|Knew It →
Write the transformation of the given function flipped, and moved one unit to the left:
Write the transformation of the given function flipped, and moved one unit to the left:
Tap to reveal answer
To transform a function horizontally, we must add or subtract the units we transform to x directly. To move left, we add units to x, which is opposite what one thinks should happen, but keep in mind that to move left is to be more negative. To flip a function, the entire function changes in sign.
After making both of these changes, we get
To transform a function horizontally, we must add or subtract the units we transform to x directly. To move left, we add units to x, which is opposite what one thinks should happen, but keep in mind that to move left is to be more negative. To flip a function, the entire function changes in sign.
After making both of these changes, we get
← Didn't Know|Knew It →