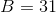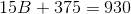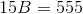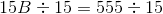Trapezoids
Help Questions
ISEE Upper Level Quantitative Reasoning › Trapezoids

Find the area of the above trapezoid if 


Figure not drawn to scale.
Explanation
The area of a trapezoid is given by

where 



Find the area of the above trapezoid if 


Figure not drawn to scale.
Explanation
The area of a trapezoid is given by

where 


A trapezoid has the base lengths of 



Explanation
The area of a trapezoid is given by

where 


A trapezoid has the base lengths of 



Explanation
The area of a trapezoid is given by

where 


In the following trapezoid 


Explanation
The area of a trapezoid is given by

where 


Substitute these values into the area formula:
In the following trapezoid 


Explanation
The area of a trapezoid is given by

where 


Substitute these values into the area formula:

Note: Figure NOT drawn to scale.
The above trapezoid has area 

Explanation
Substitute 

Note: Figure NOT drawn to scale.
The area of the above trapezoid is 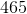

Explanation
Substitute 

Note: Figure NOT drawn to scale.
The area of the above trapezoid is 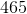

Explanation
Substitute 

Note: Figure NOT drawn to scale.
The above trapezoid has area 

Explanation
Substitute