Factors / Multiples - ISEE Upper Level Quantitative Reasoning
Card 1 of 160
What is the greatest common factor of 72 and 80?
What is the greatest common factor of 72 and 80?
Tap to reveal answer
Find the factors of 72 and 80; the greatest common factor is the greatest number in both lists.



Find the factors of 72 and 80; the greatest common factor is the greatest number in both lists.
← Didn't Know|Knew It →
What is the greatest common factor of 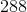 and
and  ?
?
What is the greatest common factor of 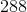

Tap to reveal answer
Fully factor 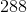 and
and  . Circle the factors in common:
. Circle the factors in common:

Multiple the common factors to find the greatest common factor:

Fully factor 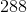


Multiple the common factors to find the greatest common factor:
← Didn't Know|Knew It →
Which of these numbers is relatively prime with 10?
Which of these numbers is relatively prime with 10?
Tap to reveal answer
We are looking for a number that shares no factors with 10 other than 1. 20 and 28 can be eliminated since 2 divides 10, 20, 28. 25 and 35 can be eliminated since 5 divides 10, 25, and 25.
21 is the correct choice;  and
and  . Since they share no prime factors,
. Since they share no prime factors,  , and 10 and 21 are relatively prime.
, and 10 and 21 are relatively prime.
We are looking for a number that shares no factors with 10 other than 1. 20 and 28 can be eliminated since 2 divides 10, 20, 28. 25 and 35 can be eliminated since 5 divides 10, 25, and 25.
21 is the correct choice; 


← Didn't Know|Knew It →
Which of these numbers is relatively prime with  ?
?
Which of these numbers is relatively prime with 
Tap to reveal answer
For a number  to be relatively prime with
to be relatively prime with  ,
,  . Equivalently,
. Equivalently,  and
and  cannot share a prime factor.
cannot share a prime factor.  , so any number that does not have either
, so any number that does not have either  or
or  as a factor is a correct choice.
as a factor is a correct choice.
We can eliminate  and
and  , since
, since  is a factor of each; we can eliminate
is a factor of each; we can eliminate  and
and  , since
, since  is a factor of each. But
is a factor of each. But  , so
, so  .
.  is the correct choice.
is the correct choice.
For a number 







We can eliminate 








← Didn't Know|Knew It →
Find the greatest common factor of 20 and 36.
Find the greatest common factor of 20 and 36.
Tap to reveal answer
To find the greatest common factor (GCF), you need to determine the factor that both numbers share that is of the greatest value. List the factors of each number and identify the largest number in value that is in both lists:


The GCF of 20 and 36 is 4 since it is the largest number in value that shows up in both lists.
To find the greatest common factor (GCF), you need to determine the factor that both numbers share that is of the greatest value. List the factors of each number and identify the largest number in value that is in both lists:
The GCF of 20 and 36 is 4 since it is the largest number in value that shows up in both lists.
← Didn't Know|Knew It →
What is the greatest common factor of 15, 30, and 40?
What is the greatest common factor of 15, 30, and 40?
Tap to reveal answer
To find the greatest common factor (GCF), you need to determine the factor that all three numbers share that is of the greatest value. List the factors of each number and identify the largest number in value that is in all three lists:



The GCF of 15, 30, and 40 is 5 since it is the largest number in value that shows up in all three lists.
To find the greatest common factor (GCF), you need to determine the factor that all three numbers share that is of the greatest value. List the factors of each number and identify the largest number in value that is in all three lists:
The GCF of 15, 30, and 40 is 5 since it is the largest number in value that shows up in all three lists.
← Didn't Know|Knew It →
What is the greatest common factor of  and
and  ?
?
What is the greatest common factor of 

Tap to reveal answer
Factor each number:

Identify the common factors ( ). The greatest common factor is the product of all of the common factors.
). The greatest common factor is the product of all of the common factors.

Factor each number:

Identify the common factors (
← Didn't Know|Knew It →
What is the greastest common factor of  and
and  ?
?
What is the greastest common factor of 

Tap to reveal answer
The greatest common factor of two numbers is the largest shared factor that the two numbers have in common.
The factors of 36 are 
The factors of 108 are 
The largest shared factor between 36 and 108 is 36. Therefore, 36 is the correct answer.
The greatest common factor of two numbers is the largest shared factor that the two numbers have in common.
The factors of 36 are
The factors of 108 are
The largest shared factor between 36 and 108 is 36. Therefore, 36 is the correct answer.
← Didn't Know|Knew It →
Find the greatest common factor (GCF) of 56 and 64.
Find the greatest common factor (GCF) of 56 and 64.
Tap to reveal answer
Find the greatest common factor (GCF) of 56 and 64.
To find the GCF, first find the prime factors of our two numbers:


Now, to find our GCF, we need to find the prime factors our two numbers have in common.
In this case, we have three 2's in common. In other words, we have an 8 in common. So, our GCF is 8.
Find the greatest common factor (GCF) of 56 and 64.
To find the GCF, first find the prime factors of our two numbers:
Now, to find our GCF, we need to find the prime factors our two numbers have in common.
In this case, we have three 2's in common. In other words, we have an 8 in common. So, our GCF is 8.
← Didn't Know|Knew It →
Find the greatest common factor (GCF) of 324 and 56.
Find the greatest common factor (GCF) of 324 and 56.
Tap to reveal answer
Find the greatest common factor (GCF) of 324 and 56.
The GCF is the largest number which will can be evenly divided from either number.
To find the GCF, first find the prime factors of both numbers. A good trick here is to start by pulling a two out of each number until you cannot pull out a two anymore.
Beginning with 56

So the prime factorization of 56 looks like:

Next, let's do 324.


So for 324 we get:

Now, the GCF can be found by taking the prime factors which are common to both numbers. Now, in this case, we have two 2's in each number, and nothing else. This means that the GCF of 56 and 324 is 
So our answer is 4
Find the greatest common factor (GCF) of 324 and 56.
The GCF is the largest number which will can be evenly divided from either number.
To find the GCF, first find the prime factors of both numbers. A good trick here is to start by pulling a two out of each number until you cannot pull out a two anymore.
Beginning with 56
So the prime factorization of 56 looks like:
Next, let's do 324.
So for 324 we get:
Now, the GCF can be found by taking the prime factors which are common to both numbers. Now, in this case, we have two 2's in each number, and nothing else. This means that the GCF of 56 and 324 is
So our answer is 4
← Didn't Know|Knew It →
What is the greatest common factor of 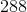 and
and 
What is the greatest common factor of 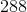
Tap to reveal answer
Fully factor 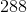 and
and  . Circle the factors in common:
. Circle the factors in common:

Multiple the common factors to find the greatest common factor:

Fully factor 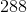


Multiple the common factors to find the greatest common factor:
← Didn't Know|Knew It →
What is the greatest common factor of 72 and 80?
What is the greatest common factor of 72 and 80?
Tap to reveal answer
Find the factors of 72 and 80; the greatest common factor is the greatest number in both lists.



Find the factors of 72 and 80; the greatest common factor is the greatest number in both lists.
← Didn't Know|Knew It →
What is the greatest common factor of 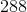 and
and  ?
?
What is the greatest common factor of 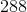

Tap to reveal answer
Fully factor 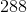 and
and  . Circle the factors in common:
. Circle the factors in common:

Multiple the common factors to find the greatest common factor:

Fully factor 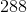


Multiple the common factors to find the greatest common factor:
← Didn't Know|Knew It →
Which of these numbers is relatively prime with 10?
Which of these numbers is relatively prime with 10?
Tap to reveal answer
We are looking for a number that shares no factors with 10 other than 1. 20 and 28 can be eliminated since 2 divides 10, 20, 28. 25 and 35 can be eliminated since 5 divides 10, 25, and 25.
21 is the correct choice;  and
and  . Since they share no prime factors,
. Since they share no prime factors,  , and 10 and 21 are relatively prime.
, and 10 and 21 are relatively prime.
We are looking for a number that shares no factors with 10 other than 1. 20 and 28 can be eliminated since 2 divides 10, 20, 28. 25 and 35 can be eliminated since 5 divides 10, 25, and 25.
21 is the correct choice; 


← Didn't Know|Knew It →
Which of these numbers is relatively prime with  ?
?
Which of these numbers is relatively prime with 
Tap to reveal answer
For a number  to be relatively prime with
to be relatively prime with  ,
,  . Equivalently,
. Equivalently,  and
and  cannot share a prime factor.
cannot share a prime factor.  , so any number that does not have either
, so any number that does not have either  or
or  as a factor is a correct choice.
as a factor is a correct choice.
We can eliminate  and
and  , since
, since  is a factor of each; we can eliminate
is a factor of each; we can eliminate  and
and  , since
, since  is a factor of each. But
is a factor of each. But  , so
, so  .
.  is the correct choice.
is the correct choice.
For a number 







We can eliminate 








← Didn't Know|Knew It →
Find the greatest common factor of 20 and 36.
Find the greatest common factor of 20 and 36.
Tap to reveal answer
To find the greatest common factor (GCF), you need to determine the factor that both numbers share that is of the greatest value. List the factors of each number and identify the largest number in value that is in both lists:


The GCF of 20 and 36 is 4 since it is the largest number in value that shows up in both lists.
To find the greatest common factor (GCF), you need to determine the factor that both numbers share that is of the greatest value. List the factors of each number and identify the largest number in value that is in both lists:
The GCF of 20 and 36 is 4 since it is the largest number in value that shows up in both lists.
← Didn't Know|Knew It →
What is the greatest common factor of 15, 30, and 40?
What is the greatest common factor of 15, 30, and 40?
Tap to reveal answer
To find the greatest common factor (GCF), you need to determine the factor that all three numbers share that is of the greatest value. List the factors of each number and identify the largest number in value that is in all three lists:



The GCF of 15, 30, and 40 is 5 since it is the largest number in value that shows up in all three lists.
To find the greatest common factor (GCF), you need to determine the factor that all three numbers share that is of the greatest value. List the factors of each number and identify the largest number in value that is in all three lists:
The GCF of 15, 30, and 40 is 5 since it is the largest number in value that shows up in all three lists.
← Didn't Know|Knew It →
What is the greatest common factor of  and
and  ?
?
What is the greatest common factor of 

Tap to reveal answer
Factor each number:

Identify the common factors ( ). The greatest common factor is the product of all of the common factors.
). The greatest common factor is the product of all of the common factors.

Factor each number:

Identify the common factors (
← Didn't Know|Knew It →
What is the greastest common factor of  and
and  ?
?
What is the greastest common factor of 

Tap to reveal answer
The greatest common factor of two numbers is the largest shared factor that the two numbers have in common.
The factors of 36 are 
The factors of 108 are 
The largest shared factor between 36 and 108 is 36. Therefore, 36 is the correct answer.
The greatest common factor of two numbers is the largest shared factor that the two numbers have in common.
The factors of 36 are
The factors of 108 are
The largest shared factor between 36 and 108 is 36. Therefore, 36 is the correct answer.
← Didn't Know|Knew It →
Find the greatest common factor (GCF) of 56 and 64.
Find the greatest common factor (GCF) of 56 and 64.
Tap to reveal answer
Find the greatest common factor (GCF) of 56 and 64.
To find the GCF, first find the prime factors of our two numbers:


Now, to find our GCF, we need to find the prime factors our two numbers have in common.
In this case, we have three 2's in common. In other words, we have an 8 in common. So, our GCF is 8.
Find the greatest common factor (GCF) of 56 and 64.
To find the GCF, first find the prime factors of our two numbers:
Now, to find our GCF, we need to find the prime factors our two numbers have in common.
In this case, we have three 2's in common. In other words, we have an 8 in common. So, our GCF is 8.
← Didn't Know|Knew It →