Numbers and Operations - ISEE Upper Level Quantitative Reasoning
Card 1 of 464
Simplify the expression:

Simplify the expression:
Tap to reveal answer
← Didn't Know|Knew It →
Simplify:

Simplify:
Tap to reveal answer
In order to add exponential terms, both the base and the exponent must be the same. So we can write:


In order to add exponential terms, both the base and the exponent must be the same. So we can write:
← Didn't Know|Knew It →
Evaluate:

Evaluate:
Tap to reveal answer
Based on the zero-exponent rule we have:

That means any non-zero number raised to the zero power is equal to  . So we can write:
. So we can write:

Based on the zero-exponent rule we have:
That means any non-zero number raised to the zero power is equal to 
← Didn't Know|Knew It →
Which of the following is equivalent to the expression below?

Which of the following is equivalent to the expression below?
Tap to reveal answer
When exponents are multiplied by one another, and the base is the same, the exponents can be added together.
The first step is to try to create a common base.

Given that the square of 2 is for, the expression can be rewritten as:


When exponents are multiplied by one another, and the base is the same, the exponents can be added together.
The first step is to try to create a common base.
Given that the square of 2 is for, the expression can be rewritten as:
← Didn't Know|Knew It →
What is the value of the expression:

What is the value of the expression:
Tap to reveal answer
When values, having the same base, are multiplied by one another, the exponents are added together and the base stays the same.
Thus,

is equal to

When values, having the same base, are multiplied by one another, the exponents are added together and the base stays the same.
Thus,
is equal to
← Didn't Know|Knew It →
Simplify: 
Simplify:
Tap to reveal answer
When multiplying exponents, the exponents are added together. Thus, 3 and 7 are added together for a sum of 10. In this problem, the "2" becomes a coefficient in front of the x. Therefore, the correct answer is:

When multiplying exponents, the exponents are added together. Thus, 3 and 7 are added together for a sum of 10. In this problem, the "2" becomes a coefficient in front of the x. Therefore, the correct answer is:
← Didn't Know|Knew It →
Simplify the expression:

Simplify the expression:
Tap to reveal answer
To simplify this problem we need to factor out a 


We can do this because multiplying exponents is the same as adding them. Therefore,



To simplify this problem we need to factor out a
We can do this because multiplying exponents is the same as adding them. Therefore,
← Didn't Know|Knew It →
Simplify:

Simplify:
Tap to reveal answer
When multiplying exponents, the exponents are added together.

When multiplying exponents, the exponents are added together.
← Didn't Know|Knew It →
Simplify:

Simplify:
Tap to reveal answer
When multiplying exponents, the exponents are added together.

When multiplying exponents, the exponents are added together.
← Didn't Know|Knew It →
Solve: 
Solve:
Tap to reveal answer
It is not necessary to evaluate both terms and multiply.
According to the rules of exponents, when we have the same bases raised to some power that are multiplied with each other, we can add the powers.

This term can be rewritten as a fraction.

The answer is: 
It is not necessary to evaluate both terms and multiply.
According to the rules of exponents, when we have the same bases raised to some power that are multiplied with each other, we can add the powers.
This term can be rewritten as a fraction.
The answer is:
← Didn't Know|Knew It →
Simplify:
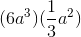
Simplify:
Tap to reveal answer
Based on the product rule for exponents in order to multiply two exponential terms with the same base, add their exponents:

So we can write:

Based on the product rule for exponents in order to multiply two exponential terms with the same base, add their exponents:
So we can write:
← Didn't Know|Knew It →
$(7-4)^{3}$=
$(7-4)^{3}$=
Tap to reveal answer
Subtract the numbers inside the parentheses first. This leaves you with 3, which you then raise to the 3rd power:
3times 3times 3=27
Subtract the numbers inside the parentheses first. This leaves you with 3, which you then raise to the 3rd power:
3times 3times 3=27
← Didn't Know|Knew It →
Evaluate:

Evaluate:
Tap to reveal answer
Any nonzero number taken to the power of 0 is equal to 1, so

Any nonzero number taken to the power of 0 is equal to 1, so
← Didn't Know|Knew It →
Multiply:

Multiply:
Tap to reveal answer
Use the FOIL method:






Use the FOIL method:
← Didn't Know|Knew It →
Simplify:

Simplify:
Tap to reveal answer
Based on the power rule, we know that in order to raise a power to a power we need to multiply the exponents, i.e.
 .
.

Based on the power rule, we know that in order to raise a power to a power we need to multiply the exponents, i.e.

← Didn't Know|Knew It →
Simplify:

Simplify:
Tap to reveal answer
The Negative Exponent Rule says  .
.

The power rule says that, in order to raise a power to a power, we need to multiply the exponents, i.e.  .
.

The Negative Exponent Rule says 
The power rule says that, in order to raise a power to a power, we need to multiply the exponents, i.e. 
← Didn't Know|Knew It →
Simplify:
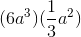
Simplify:
Tap to reveal answer
Based on the product rule for exponents in order to multiply two exponential terms with the same base, add their exponents:

So we can write:

Based on the product rule for exponents in order to multiply two exponential terms with the same base, add their exponents:
So we can write:
← Didn't Know|Knew It →
Evaluate:

Evaluate:
Tap to reveal answer
Based on the power rule for exponents we can write:

That means; to raise a power to a power we need to multiply the exponents. In addition, based on the product rule for exponents in order to multiply two exponential terms with the same base, we need to add their exponents:

So we can write:

Based on the power rule for exponents we can write:
That means; to raise a power to a power we need to multiply the exponents. In addition, based on the product rule for exponents in order to multiply two exponential terms with the same base, we need to add their exponents:
So we can write:
← Didn't Know|Knew It →
Evaluate:

Evaluate:
Tap to reveal answer
Based on the negative exponent rule we have:

which says negative exponents in the numerator get moved to the denominator and become positive exponents. And negative exponents in the denominator get moved to the numerator and become positive exponents. So we can write:

In addition, based on the power rule for exponents we can write:

That means; to raise a power to a power we need to multiply the exponents. We also know that when a fraction is raised to a power, the numerator and the denominator are both raised to that power. So we can write:





Based on the negative exponent rule we have:
which says negative exponents in the numerator get moved to the denominator and become positive exponents. And negative exponents in the denominator get moved to the numerator and become positive exponents. So we can write:
In addition, based on the power rule for exponents we can write:
That means; to raise a power to a power we need to multiply the exponents. We also know that when a fraction is raised to a power, the numerator and the denominator are both raised to that power. So we can write:
← Didn't Know|Knew It →
Evaluate:

Evaluate:
Tap to reveal answer
Based on the power rule for exponents we can write:

That means; to raise a power to a power we need to multiply the exponents. In addition, based on the product rule for exponents, in order to multiply two exponential terms with the same base we need to add their exponents:

So we can write:

in order to divide two exponents with the same base, we can keep the base and subtract the powers. So we get:

Based on the power rule for exponents we can write:
That means; to raise a power to a power we need to multiply the exponents. In addition, based on the product rule for exponents, in order to multiply two exponential terms with the same base we need to add their exponents:
So we can write:
in order to divide two exponents with the same base, we can keep the base and subtract the powers. So we get:
← Didn't Know|Knew It →

