Acute / Obtuse Isosceles Triangles - ISEE Upper Level Quantitative Reasoning
Card 1 of 12
Two sides of an isosceles triangle have lengths 3 feet and 4 feet. Which of the following could be the length of the third side?
Two sides of an isosceles triangle have lengths 3 feet and 4 feet. Which of the following could be the length of the third side?
Tap to reveal answer
An isosceles triangle, by definition, has two sides of equal length. Having the third side measure either 3 feet or 4 feet would make the triangle meet this criterion.
3 feet is equal to  inches, and 4 feet is equal to
inches, and 4 feet is equal to  inches. We choose 36 inches, since that, but not 48 inches, is a choice.
inches. We choose 36 inches, since that, but not 48 inches, is a choice.
An isosceles triangle, by definition, has two sides of equal length. Having the third side measure either 3 feet or 4 feet would make the triangle meet this criterion.
3 feet is equal to 

← Didn't Know|Knew It →
The triangles are similar. Solve for  .
.

The triangles are similar. Solve for 

Tap to reveal answer
Because the triangles are similar, proportions can be used to solve for the length of the side:

Cross-multiply:


Because the triangles are similar, proportions can be used to solve for the length of the side:
Cross-multiply:
← Didn't Know|Knew It →
One of the base angles of an isosceles triangle is  . Give the measure of the vertex angle.
. Give the measure of the vertex angle.
One of the base angles of an isosceles triangle is 
Tap to reveal answer
The base angles of an isosceles triangle are always equal. Therefore both base angles are  .
.
Let  the measure of the third angle. Since the sum of the angles of a triangle is
the measure of the third angle. Since the sum of the angles of a triangle is 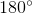 , we can solve accordingly:
, we can solve accordingly:

The base angles of an isosceles triangle are always equal. Therefore both base angles are 
Let 
← Didn't Know|Knew It →
One of the base angles of an isosceles triangle is  . Give the measure of the vertex angle.
. Give the measure of the vertex angle.
One of the base angles of an isosceles triangle is 
Tap to reveal answer
The base angles of an isosceles triangle are always equal. Therefore both base angles are  .
.
Let  the measure of the third angle. Since the sum of the angles of a triangle is
the measure of the third angle. Since the sum of the angles of a triangle is 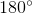 , we can solve accordingly:
, we can solve accordingly:

The base angles of an isosceles triangle are always equal. Therefore both base angles are 
Let 
← Didn't Know|Knew It →
One of the base angles of an isosceles triangle is  . Give the measure of the vertex angle.
. Give the measure of the vertex angle.
One of the base angles of an isosceles triangle is 
Tap to reveal answer
The base angles of an isosceles triangle are always equal. Therefore both base angles are  .
.
Let  the measure of the third angle. Since the sum of the angles of a triangle is
the measure of the third angle. Since the sum of the angles of a triangle is 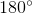 , we can solve accordingly:
, we can solve accordingly:

The base angles of an isosceles triangle are always equal. Therefore both base angles are 
Let 
← Didn't Know|Knew It →
Two sides of an isosceles triangle have lengths 3 feet and 4 feet. Which of the following could be the length of the third side?
Two sides of an isosceles triangle have lengths 3 feet and 4 feet. Which of the following could be the length of the third side?
Tap to reveal answer
An isosceles triangle, by definition, has two sides of equal length. Having the third side measure either 3 feet or 4 feet would make the triangle meet this criterion.
3 feet is equal to  inches, and 4 feet is equal to
inches, and 4 feet is equal to  inches. We choose 36 inches, since that, but not 48 inches, is a choice.
inches. We choose 36 inches, since that, but not 48 inches, is a choice.
An isosceles triangle, by definition, has two sides of equal length. Having the third side measure either 3 feet or 4 feet would make the triangle meet this criterion.
3 feet is equal to 

← Didn't Know|Knew It →
The triangles are similar. Solve for  .
.

The triangles are similar. Solve for 

Tap to reveal answer
Because the triangles are similar, proportions can be used to solve for the length of the side:

Cross-multiply:


Because the triangles are similar, proportions can be used to solve for the length of the side:
Cross-multiply:
← Didn't Know|Knew It →
Two sides of an isosceles triangle have lengths 3 feet and 4 feet. Which of the following could be the length of the third side?
Two sides of an isosceles triangle have lengths 3 feet and 4 feet. Which of the following could be the length of the third side?
Tap to reveal answer
An isosceles triangle, by definition, has two sides of equal length. Having the third side measure either 3 feet or 4 feet would make the triangle meet this criterion.
3 feet is equal to  inches, and 4 feet is equal to
inches, and 4 feet is equal to  inches. We choose 36 inches, since that, but not 48 inches, is a choice.
inches. We choose 36 inches, since that, but not 48 inches, is a choice.
An isosceles triangle, by definition, has two sides of equal length. Having the third side measure either 3 feet or 4 feet would make the triangle meet this criterion.
3 feet is equal to 

← Didn't Know|Knew It →
The triangles are similar. Solve for  .
.

The triangles are similar. Solve for 

Tap to reveal answer
Because the triangles are similar, proportions can be used to solve for the length of the side:

Cross-multiply:


Because the triangles are similar, proportions can be used to solve for the length of the side:
Cross-multiply:
← Didn't Know|Knew It →
Two sides of an isosceles triangle have lengths 3 feet and 4 feet. Which of the following could be the length of the third side?
Two sides of an isosceles triangle have lengths 3 feet and 4 feet. Which of the following could be the length of the third side?
Tap to reveal answer
An isosceles triangle, by definition, has two sides of equal length. Having the third side measure either 3 feet or 4 feet would make the triangle meet this criterion.
3 feet is equal to  inches, and 4 feet is equal to
inches, and 4 feet is equal to  inches. We choose 36 inches, since that, but not 48 inches, is a choice.
inches. We choose 36 inches, since that, but not 48 inches, is a choice.
An isosceles triangle, by definition, has two sides of equal length. Having the third side measure either 3 feet or 4 feet would make the triangle meet this criterion.
3 feet is equal to 

← Didn't Know|Knew It →
The triangles are similar. Solve for  .
.

The triangles are similar. Solve for 

Tap to reveal answer
Because the triangles are similar, proportions can be used to solve for the length of the side:

Cross-multiply:


Because the triangles are similar, proportions can be used to solve for the length of the side:
Cross-multiply:
← Didn't Know|Knew It →
One of the base angles of an isosceles triangle is  . Give the measure of the vertex angle.
. Give the measure of the vertex angle.
One of the base angles of an isosceles triangle is 
Tap to reveal answer
The base angles of an isosceles triangle are always equal. Therefore both base angles are  .
.
Let  the measure of the third angle. Since the sum of the angles of a triangle is
the measure of the third angle. Since the sum of the angles of a triangle is 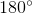 , we can solve accordingly:
, we can solve accordingly:

The base angles of an isosceles triangle are always equal. Therefore both base angles are 
Let 
← Didn't Know|Knew It →