How to find if right triangles are similar - ISEE Upper Level Quantitative Reasoning
Card 1 of 4

 is a right angle;
is a right angle;  ,
,  .
.
Which is the greater quantity?
(a) 
(b) 



Which is the greater quantity?
(a)
(b)
Tap to reveal answer
 . Corresponding angles of similar triangles are congruent, so since
. Corresponding angles of similar triangles are congruent, so since  is a right angle, so is
is a right angle, so is  .
.
The hypotenuse  of
of  is twice as long as leg
is twice as long as leg  ; by the
; by the  Theorem,
Theorem, 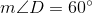 . Again, by similiarity,
. Again, by similiarity,
 .
.



The hypotenuse 




← Didn't Know|Knew It →

 is a right angle;
is a right angle;  ,
,  .
.
Which is the greater quantity?
(a) 
(b) 



Which is the greater quantity?
(a)
(b)
Tap to reveal answer
 . Corresponding angles of similar triangles are congruent, so since
. Corresponding angles of similar triangles are congruent, so since  is a right angle, so is
is a right angle, so is  .
.
The hypotenuse  of
of  is twice as long as leg
is twice as long as leg  ; by the
; by the  Theorem,
Theorem, 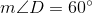 . Again, by similiarity,
. Again, by similiarity,
 .
.



The hypotenuse 




← Didn't Know|Knew It →

 is a right angle;
is a right angle;  ,
,  .
.
Which is the greater quantity?
(a) 
(b) 



Which is the greater quantity?
(a)
(b)
Tap to reveal answer
 . Corresponding angles of similar triangles are congruent, so since
. Corresponding angles of similar triangles are congruent, so since  is a right angle, so is
is a right angle, so is  .
.
The hypotenuse  of
of  is twice as long as leg
is twice as long as leg  ; by the
; by the  Theorem,
Theorem, 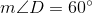 . Again, by similiarity,
. Again, by similiarity,
 .
.



The hypotenuse 




← Didn't Know|Knew It →

 is a right angle;
is a right angle;  ,
,  .
.
Which is the greater quantity?
(a) 
(b) 



Which is the greater quantity?
(a)
(b)
Tap to reveal answer
 . Corresponding angles of similar triangles are congruent, so since
. Corresponding angles of similar triangles are congruent, so since  is a right angle, so is
is a right angle, so is  .
.
The hypotenuse  of
of  is twice as long as leg
is twice as long as leg  ; by the
; by the  Theorem,
Theorem, 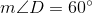 . Again, by similiarity,
. Again, by similiarity,
 .
.



The hypotenuse 




← Didn't Know|Knew It →