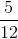How to add fractions

Help Questions

ISEE Middle Level Quantitative Reasoning › How to add fractions

Questions 1 - 10

Untitled

The square and the triangle in the above diagram are both equally divided. Which is the greater quantity?

(a) The fraction of the square that is shaded

(b) The fraction of the triangle that is shaded

(a) and (b) are equal

(b) is the greater quantity

(a) is the greater quantity

It is impossible to determine which is greater from the information given

Explanation

The square is divided into eighteen triangles of equal size and shape; nine are shaded, so the fraction of the square that is shaded is

$\frac{9}{18} = \frac{9 \div 9 }{18\div 9 } = \frac{1}{2}$

The triangle is divided into sixteen triangles of equal size and shape; eight are shaded, so the fraction of the square that is shaded is

$\frac{8}{16} = \frac{8 \div 8 }{16 \div 8 } = \frac{1}{2}$ .

The fractions are equal.

Figures 1

Refer to the above diagrams. Each figure is divided into sections of equal size and shape.

Which is the greater quantity?

(a) The fraction of Figure 1 that is shaded

(b) The fraction of Figure 2 that is shaded

(a) is the greater quantity

(a) and (b) are equal

It is impossible to determine which is greater from the information given

(b) is the greater quantity

Explanation

Figure 1 is a rectangle divided into 24 squares of equal size; 8 of the squares are shaded, which means that $\frac{8}{24}$ of Figure 1 is shaded.

Figure 2 is a triangle divided into 4 triangles of equal size; 1 is shaded, which means that $\frac{1}{4} = \frac{1 \times 6 }{4 \times 6} =\frac{6}{24 }$ of Figure 2 is shaded.

The fraction of Figure 1 that is shaded is the greater quantity.

Add:

$\frac{6}{61}+\frac{11}{61}=$

$\frac{17}{61}$

$\frac{5}{61}$

$\frac{66}{61}$

$\frac{61}{17}$

Explanation

Add the numerators and leave the denominators the same:

$\frac{6}{61}+\frac{11}{61}=\frac{17}{61}$

Answer:

$\frac{17}{61}$

On Thursday it snowed $\frac{2}{12}$ of an inch in the afternoon and $\frac{1}{12}$ of an inch in the evening. What was the total amount of snowfall on Thursday?

$\frac{3}{12}$

$\frac{4}{12}$

$\frac{5}{12}$

$\frac{6}{12}$

$\frac{7}{12}$

Explanation

To solve this problem, we are putting the amount of snowfall from the afternoon and the evening together, so we add the fractions.

$\frac{2}{12}+\frac{1}{12}=\frac{3}{12}$

3 12

Column A Column B

$\frac{2}{5}+\frac{1}{2}$ $\frac{1}{9}+\frac{7}{8}$

The quantity in Column B is greater.

The quantity in Column A is greater.

The quantities in each column are equal.

There is no way to determine the relationship between the quantities in the columns.

Explanation

First, you must add the fractions in each column. When adding fractions, find the common denominator. The common denominator for Column A is 10. Then, change the numerators to reflect changing the denominators to give you $\frac{4}{10}+\frac{5}{10}$ . Combie the numerators to give you $\frac{9}{10}.$ Then, add the fractions in Column B. The common denominator for those fractions is 72. Therefore, you get $\frac{8}{72}+\frac{63}{72}$ . Combine the numerators to get $\frac{71}{72}$ . Compare those two fractions. Think of them as slices of pizza. There would be way more of Column B. Therefore, it is greater. Also, a little to trick to comparing fractions is cross-multiply. The side that has the biggest product is the greatest.

is a positive integer. Which is the greater quantity?

(a) $A + \frac{3}{4}$

(b) $A \cdot \frac{3}{4}$

(a) is the greater quantity

(b) is the greater quantity

(a) and (b) are equal

It is impossible to determine which is greater from the information given

Explanation

$\frac{3}{4} < 1$ and is positive, so by the multiplication property of inequality,

$\frac{3}{4} \cdot A < 1 \cdot A$

$\frac{3}{4} A < A$

Also,

$A < A + \frac{3}{4 }$ ,

$\frac{3}{4} A < A+ \frac{3}{4 }$

Solve the following:

$\frac{7}{8} - \frac{3}{8}$

$\frac{1}{2}$

$\frac{4}{0}$

$\frac{4}{1}$

$\frac{10}{16}$

$\frac{1}{3}$

Explanation

To subtract fractions, we need to find a common denominator, then we subtract the numerators only.

So, given the problem

$\frac{7}{8} - \frac{3}{8}$

we can see we already have a common denominator. So, we will now subtract the numerators (note that we will leave the denominator alone). We get

$\frac{7-3}{8}$

$\frac{4}{8}$

$\frac{1}{2}$

Add:

$\frac{3}{27}+\frac{10}{27}=$

$\frac{13}{27}$

$\frac{3}{27}$

$\frac{10}{27}$

$\frac{7}{27}$

Explanation

To solve, add the numerators and leave the denominators the same:

$\frac{3}{27}+\frac{10}{27}=\frac{13}{27}$

Answer:

$\frac{13}{27}$

Assorted 2

Which is the greater quantity?

(a) The fraction of the circles that are shaded

(b) The fraction of the squares that are shaded

(a) and (b) are equal

(a) is the greater quantity

(b) is the greater quantity

It is impossible to determine which is greater from the information given

Explanation

1 of the 4 circles in the diagram - $\frac{1}{4}$ of the circles - are shaded, as are 2 of the 8 squares - $\frac{2}{8} = \frac{2 \div 2}{8 \div 2} = \frac{1}{4}$ of them.

On Tuesday it snowed $\frac{6}{12}$ of an inch in the afternoon and $\frac{2}{12}$ of an inch in the evening. What was the total amount of snowfall on Tuesday?