Induction

Help Questions

Introduction to Analysis › Induction

Questions 1 - 1

Determine whether the following statement is true or false:

If 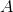is a nonempty subset of $\mathbb{N}$ , then has a finite infimum and it is an element of .

True

False

According to the Well-Ordered Principal this statement is true. The following proof illuminate its truth.

Suppose $A\subseteq \mathbb{N}$ is nonempty. From there, it is known that is bounded above, by .

Therefore, by the Completeness Axiom the supremum of exists.

Furthermore, if $A\subset \mathbb{Z}$ has a supremum, then $\text{sup}A\ \epsilon\ A$ , thus in this particular case $\text{sup}(-A)\ \epsilon\ -A$ .

Thus by the Reflection Principal,

$\text{inf}A=-\text{sup}(-A)$

exists and

$\text{inf}A\ \epsilon\ -(-A)=A$ .

Therefore proving the statement in question true.