Limits of Sequences - Introduction to Analysis
Card 0 of 4
What term does the following define.
A sequence of sets 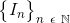 is if and only if
is if and only if  .
.
What term does the following define.
A sequence of sets 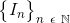

This statement:
A sequence of sets  is if and only if
is if and only if 
is the definition of nested.
This means that the sequence 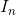 for all
for all  elements, for which
elements, for which  belongs to the natural numbers, is considered a nested set if and only if the subsequent sets are subsets of it.
belongs to the natural numbers, is considered a nested set if and only if the subsequent sets are subsets of it.
Other theorems in intro analysis build off this understanding.
This statement:
A sequence of sets 
is the definition of nested.
This means that the sequence 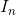


Other theorems in intro analysis build off this understanding.
Compare your answer with the correct one above
What term does the following define.
A sequence of sets 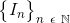 is if and only if
is if and only if  .
.
What term does the following define.
A sequence of sets 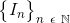

This statement:
A sequence of sets  is if and only if
is if and only if 
is the definition of nested.
This means that the sequence 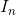 for all
for all  elements, for which
elements, for which  belongs to the natural numbers, is considered a nested set if and only if the subsequent sets are subsets of it.
belongs to the natural numbers, is considered a nested set if and only if the subsequent sets are subsets of it.
Other theorems in intro analysis build off this understanding.
This statement:
A sequence of sets 
is the definition of nested.
This means that the sequence 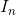


Other theorems in intro analysis build off this understanding.
Compare your answer with the correct one above
What term does the following define.
A sequence of sets 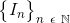 is if and only if
is if and only if  .
.
What term does the following define.
A sequence of sets 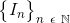

This statement:
A sequence of sets  is if and only if
is if and only if 
is the definition of nested.
This means that the sequence 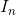 for all
for all  elements, for which
elements, for which  belongs to the natural numbers, is considered a nested set if and only if the subsequent sets are subsets of it.
belongs to the natural numbers, is considered a nested set if and only if the subsequent sets are subsets of it.
Other theorems in intro analysis build off this understanding.
This statement:
A sequence of sets 
is the definition of nested.
This means that the sequence 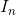


Other theorems in intro analysis build off this understanding.
Compare your answer with the correct one above
What term does the following define.
A sequence of sets 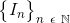 is if and only if
is if and only if  .
.
What term does the following define.
A sequence of sets 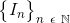

This statement:
A sequence of sets  is if and only if
is if and only if 
is the definition of nested.
This means that the sequence 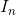 for all
for all  elements, for which
elements, for which  belongs to the natural numbers, is considered a nested set if and only if the subsequent sets are subsets of it.
belongs to the natural numbers, is considered a nested set if and only if the subsequent sets are subsets of it.
Other theorems in intro analysis build off this understanding.
This statement:
A sequence of sets 
is the definition of nested.
This means that the sequence 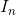


Other theorems in intro analysis build off this understanding.
Compare your answer with the correct one above