Four Vectors - GRE Subject Test: Physics
Card 1 of 8
A container of water is carried on a space ship traveling at 60% the speed of light relative to the Earth. From the perspective of an observer on Earth, what is the speed of the light in the water?

A container of water is carried on a space ship traveling at 60% the speed of light relative to the Earth. From the perspective of an observer on Earth, what is the speed of the light in the water?
Tap to reveal answer
The speed of light through water in a stationary frame is found from the index of refraction of water, which is approximately 

To find the relative speed, use the following equation:


The speed of light through water in a stationary frame is found from the index of refraction of water, which is approximately
To find the relative speed, use the following equation:
← Didn't Know|Knew It →
A reference frame S' is moving at 0.6_c_ in the z direction with respect to a stationary frame S. An event occurs in S' with the coordinates (x', y', z', ct')=(1, 0, 2, 3). What are the coordinates (x, y, z, ct) of the event with respect to the stationary frame S?
A reference frame S' is moving at 0.6_c_ in the z direction with respect to a stationary frame S. An event occurs in S' with the coordinates (x', y', z', ct')=(1, 0, 2, 3). What are the coordinates (x, y, z, ct) of the event with respect to the stationary frame S?
Tap to reveal answer
To apply a Lorentz transformation, we need gamma and beta:
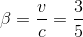
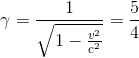
Then, apply the Lorentz transformation:
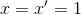

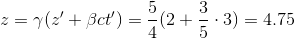

To apply a Lorentz transformation, we need gamma and beta:
Then, apply the Lorentz transformation:
← Didn't Know|Knew It →
A container of water is carried on a space ship traveling at 60% the speed of light relative to the Earth. From the perspective of an observer on Earth, what is the speed of the light in the water?

A container of water is carried on a space ship traveling at 60% the speed of light relative to the Earth. From the perspective of an observer on Earth, what is the speed of the light in the water?
Tap to reveal answer
The speed of light through water in a stationary frame is found from the index of refraction of water, which is approximately 

To find the relative speed, use the following equation:


The speed of light through water in a stationary frame is found from the index of refraction of water, which is approximately
To find the relative speed, use the following equation:
← Didn't Know|Knew It →
A reference frame S' is moving at 0.6_c_ in the z direction with respect to a stationary frame S. An event occurs in S' with the coordinates (x', y', z', ct')=(1, 0, 2, 3). What are the coordinates (x, y, z, ct) of the event with respect to the stationary frame S?
A reference frame S' is moving at 0.6_c_ in the z direction with respect to a stationary frame S. An event occurs in S' with the coordinates (x', y', z', ct')=(1, 0, 2, 3). What are the coordinates (x, y, z, ct) of the event with respect to the stationary frame S?
Tap to reveal answer
To apply a Lorentz transformation, we need gamma and beta:
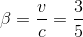
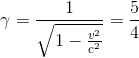
Then, apply the Lorentz transformation:
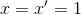

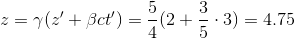

To apply a Lorentz transformation, we need gamma and beta:
Then, apply the Lorentz transformation:
← Didn't Know|Knew It →
A container of water is carried on a space ship traveling at 60% the speed of light relative to the Earth. From the perspective of an observer on Earth, what is the speed of the light in the water?

A container of water is carried on a space ship traveling at 60% the speed of light relative to the Earth. From the perspective of an observer on Earth, what is the speed of the light in the water?
Tap to reveal answer
The speed of light through water in a stationary frame is found from the index of refraction of water, which is approximately 

To find the relative speed, use the following equation:


The speed of light through water in a stationary frame is found from the index of refraction of water, which is approximately
To find the relative speed, use the following equation:
← Didn't Know|Knew It →
A reference frame S' is moving at 0.6_c_ in the z direction with respect to a stationary frame S. An event occurs in S' with the coordinates (x', y', z', ct')=(1, 0, 2, 3). What are the coordinates (x, y, z, ct) of the event with respect to the stationary frame S?
A reference frame S' is moving at 0.6_c_ in the z direction with respect to a stationary frame S. An event occurs in S' with the coordinates (x', y', z', ct')=(1, 0, 2, 3). What are the coordinates (x, y, z, ct) of the event with respect to the stationary frame S?
Tap to reveal answer
To apply a Lorentz transformation, we need gamma and beta:
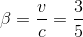
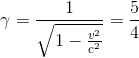
Then, apply the Lorentz transformation:
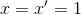

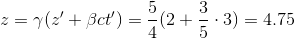

To apply a Lorentz transformation, we need gamma and beta:
Then, apply the Lorentz transformation:
← Didn't Know|Knew It →
A container of water is carried on a space ship traveling at 60% the speed of light relative to the Earth. From the perspective of an observer on Earth, what is the speed of the light in the water?

A container of water is carried on a space ship traveling at 60% the speed of light relative to the Earth. From the perspective of an observer on Earth, what is the speed of the light in the water?
Tap to reveal answer
The speed of light through water in a stationary frame is found from the index of refraction of water, which is approximately 

To find the relative speed, use the following equation:


The speed of light through water in a stationary frame is found from the index of refraction of water, which is approximately
To find the relative speed, use the following equation:
← Didn't Know|Knew It →
A reference frame S' is moving at 0.6_c_ in the z direction with respect to a stationary frame S. An event occurs in S' with the coordinates (x', y', z', ct')=(1, 0, 2, 3). What are the coordinates (x, y, z, ct) of the event with respect to the stationary frame S?
A reference frame S' is moving at 0.6_c_ in the z direction with respect to a stationary frame S. An event occurs in S' with the coordinates (x', y', z', ct')=(1, 0, 2, 3). What are the coordinates (x, y, z, ct) of the event with respect to the stationary frame S?
Tap to reveal answer
To apply a Lorentz transformation, we need gamma and beta:
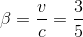
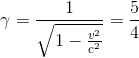
Then, apply the Lorentz transformation:
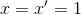

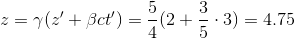

To apply a Lorentz transformation, we need gamma and beta:
Then, apply the Lorentz transformation:
← Didn't Know|Knew It →