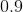How to find the square root of a decimal
Help Questions
GRE Quantitative Reasoning › How to find the square root of a decimal
Solve for 
Explanation
Just like any other equation, isolate your variable. Start by multiplying both sides by 
Now, this is the same as:
You know that 


Find the square root of the following decimal:
Explanation
This problem can be solve more easily by rewriting the decimal into scientific notation.
Because 
Find the square root of the following decimal:
Explanation
To find the square root of this decimal we convert it into scientific notation.
Because 
Find the square root of the following decimal:
Explanation
To find the square root of this decimal we convert it into scientific notation.
Because 
Find the square root of the following decimal:
Explanation
To find the square root of this decimal we convert it into scientific notation.
Because 
Find the square root of the following decimal:
Explanation
To find the square root of this decimal we convert it into scientific notation.
Because 


Find the square root of the following decimal:
Explanation
This problem becomes much simpler if we rewrite the decimal in scientific notation
Because 
Find the square root of the following decimal:
Explanation
To find the square root of this decimal we convert it into scientific notation.
Because 


Find the square root of the following decimal:
Explanation
To find the square root of this decimal we convert it into scientific notation.
Because 
Find the square root of the following decimal:
Explanation
The easiest way to find the square root of a fraction is to convert it into scientific notation.
The key is that the exponent in scientific notation has to be even for a square root because the square root of an exponent is diving it by two. The square root of 9 is 3, so the square root of 8.1 is a little bit less than 3, around 2.8