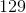GRE Quantitative Reasoning - How to find the nth term of an arithmetic sequence

Let Z represent a sequence of numbers wherein each term is defined as seven less than three times the preceding term. If , what is the first term in the sequence?

Explanation

Let us first write the value of a consecutive term in a numerical format:

$z_{n+1} = 3z_n-7$

Consequently,

$z_n=\frac{z_{n+1}+7}{3}$

Using the first equation, we can define in terms of :

This allows us to rewrite

Rearrangement of terms allows us to solve for :

Now, using our second equation, we can find , the first term:

$z_{1}=\frac{z_2+7}{3}=\frac{\frac{z_{3}+7}{3}+7}{3}=\frac{\frac{24}{3}+7}{3}=\frac{15}{3}=5$

The first term in a sequence of integers is 2 and the second term is 10. All subsequent terms are the arithmetic mean of all of the preceding terms. What is the 39th term?

300

600

1200

Explanation

The first term and second term average out to 6. So the third term is 6. Now add 6 to the preceding two terms and divide by 3 to get the average of the first three terms, which is the value of the 4th term. This, too, is 6 (18/3)—all terms after the 2nd are 6, including the 39th. Thus, the answer is 6.

In a sequence of numbers, the first two values are 1 and 2. Each successive integer is calculated by adding the previous two and mutliplying that result by 3. What is fifth value in this sequence?