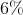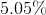GRE Quantitative Reasoning - How to find simple interest

What is the simple interest rate on an account that accrued after a year if the original deposit was ? Round your answer to the nearest hundredth.

Explanation

The easiest way to do this is to translate the question into "is / of language." The question is asking, "What percentage of is ?" Remember, is means equals and of indicates multiplication. "What" means a variable like . Therefore, we can rewrite our sentence as:

$x\cdot7505=450$

Solving for , we get:

$x=\frac{450}{7505}=0.0599600266489$

This is %. Rounding to the nearest hudredth, you get or .

If a student borrows $200,000 at an interest rate of 6% compounded annually, when she graduates in 4 years how much money will she owe? Round to the nearest dollar.

$252,495

$265,432

$264,432

$257,543

$243,432

Explanation

This problem requires knowledge of the compound interest formula, $A=P(1+\frac{r}{n})^{nt}$ .

Where is the amount of money owed, is the sum borrowed, is the yearly interest rate, is the amount of times the interest is compounded per year, and is the number of years. We know that the student borrowed $200,000 compounded annually at a %6 interest rate, therefore by plugging in those numbers we find that after she graduates in 4 years she will owe $252,495.

Harry borrowed $5000 from his parents at a rate of simple interest of 2% annually and paid it back in full in 30 months. What is the total amount of interest and principal his parents charged him?

none of these

Explanation

Principal = $5000 (original amount)

Interest = 30 months = 2 years and a half

$$5000 \cdot 2%=$100\cdot 2\ years=$200$

half a year's interest is

Total interest =

What is the interest rate on an account if an original balance of rises to after one year if it is only compounded yearly?

Explanation

You can solve this by using the standard formula for simple interest (which is merely a derivative of standard applications of the formulas used for percentages in general). For our problem this is:

$(1+r)\cdot12050=12670$