Squares - GRE Quantitative Reasoning
Card 1 of 160
If a square has a side length of √2, how long is the diagonal of the square?
If a square has a side length of √2, how long is the diagonal of the square?
Tap to reveal answer
A diagonal divides a square into two 45-45-90 triangles, which have lengths adhering to the ratio of x: x: x√2. Therefore, 2 is the correct answer as the diagonal represents the hypotenuse of the triangle. the Pythagorean theorem can also be used: √22+ √22 = c2.
A diagonal divides a square into two 45-45-90 triangles, which have lengths adhering to the ratio of x: x: x√2. Therefore, 2 is the correct answer as the diagonal represents the hypotenuse of the triangle. the Pythagorean theorem can also be used: √22+ √22 = c2.
← Didn't Know|Knew It →
If a square has a side length of 4, how long is the diagonal of the square?
If a square has a side length of 4, how long is the diagonal of the square?
Tap to reveal answer
A diagonal divides a square into two 45-45-90 triangles, which have lengths adhering to the ratio of x: x: x√2. Therefore, 4√2 is the correct answer as the diagonal represents the hypotenuse of the triangle. the Pythagorean theorem can also be used: 42+ 42 = c2.
A diagonal divides a square into two 45-45-90 triangles, which have lengths adhering to the ratio of x: x: x√2. Therefore, 4√2 is the correct answer as the diagonal represents the hypotenuse of the triangle. the Pythagorean theorem can also be used: 42+ 42 = c2.
← Didn't Know|Knew It →
A square has a side of length 5. What is the length of its diagonal?
A square has a side of length 5. What is the length of its diagonal?
Tap to reveal answer
The diagonal separates the square into two 45-45-90 right triangles. The problem can be solved by using the Pythagorean Theorem, _a_2 + _b_2 = _c_2. It can also be solved by recognizing the 45-45-90 special triangles, which have side ratios of x : x : x√2.
The diagonal separates the square into two 45-45-90 right triangles. The problem can be solved by using the Pythagorean Theorem, _a_2 + _b_2 = _c_2. It can also be solved by recognizing the 45-45-90 special triangles, which have side ratios of x : x : x√2.
← Didn't Know|Knew It →
A square with width of  is inscribed in a circle. What is the total area inside the circle?
is inscribed in a circle. What is the total area inside the circle?
A square with width of 
Tap to reveal answer
We know that each side of the square is 6, so use the Pythagorean Theorem to solve for the diagonal of the square. The diagonal of the square is also the diameter of the circle.
$6^{2}$$+6^{2}$ = $d^{2}$
72= $d^{2}$
$\sqrt{72}$=d
$\sqrt{72}$=$\sqrt{36times 2}$=6$\sqrt{2}$
6$\sqrt{2}$=d
Therefore the radius must be r=\frac{6sqrt{2}$}{2}rightarrow 3$\sqrt{2}$
Now let's find the area inside the circle using the radius.
A=pi $r^{2}$
A=pileft (3$\sqrt{2}$ right $)^{2}$
A=pileft (3$\sqrt{2}$ right $)^{2}$rightarrow pileft ( 9times 2 right )rightarrow 18pi
A=18pi meters2
We know that each side of the square is 6, so use the Pythagorean Theorem to solve for the diagonal of the square. The diagonal of the square is also the diameter of the circle.
$6^{2}$$+6^{2}$ = $d^{2}$
72= $d^{2}$
$\sqrt{72}$=d
$\sqrt{72}$=$\sqrt{36times 2}$=6$\sqrt{2}$
6$\sqrt{2}$=d
Therefore the radius must be r=\frac{6sqrt{2}$}{2}rightarrow 3$\sqrt{2}$
Now let's find the area inside the circle using the radius.
A=pi $r^{2}$
A=pileft (3$\sqrt{2}$ right $)^{2}$
A=pileft (3$\sqrt{2}$ right $)^{2}$rightarrow pileft ( 9times 2 right )rightarrow 18pi
A=18pi meters2
← Didn't Know|Knew It →
Quantity A:
The diagonal of a square with a side-length of  .
.
Quantity B:
The side-length of a square with a diagonal of  .
.
Quantity A:
The diagonal of a square with a side-length of 
Quantity B:
The side-length of a square with a diagonal of 
Tap to reveal answer
Quantity A: The diagonal of a square with a side-length of 7.
Quantity B: The side-length of a square with a diagonal of 14.
Both quantities can be determined, so can the relationship.
Quantity A:
To determine the diagonal of a square, it's important to remember that a diagonal directly bisects a square from corner to corner. In other words, it bisects the corners, creating two triangles with 45:45:90 proportions, with the diagonal serving as the hypotenuses . If you remember your special triangles, then the side-side-hypotenuse measurements have a ratio of  .
.
In Quantity A, the side-length is 7. Following the proportion:

The diagonal equals  .
.
Quantity B:
We can use the same ratio to figure out quantity B by substituting x for the unknown side-length quantity, which looks like this:

To find x in this ratio, just isolate x in the hypotenuse:

Divide by 

Now, how does Quantity A and Quantity B match up?


On the surface, it looks like the two quanties are equal. But how do we prove it? Well, we know that  . Therefore, we know that:
. Therefore, we know that:

Divide both sides by 

Therefore, both quantities are equal.
Quantity A: The diagonal of a square with a side-length of 7.
Quantity B: The side-length of a square with a diagonal of 14.
Both quantities can be determined, so can the relationship.
Quantity A:
To determine the diagonal of a square, it's important to remember that a diagonal directly bisects a square from corner to corner. In other words, it bisects the corners, creating two triangles with 45:45:90 proportions, with the diagonal serving as the hypotenuses . If you remember your special triangles, then the side-side-hypotenuse measurements have a ratio of 
In Quantity A, the side-length is 7. Following the proportion:
The diagonal equals 
Quantity B:
We can use the same ratio to figure out quantity B by substituting x for the unknown side-length quantity, which looks like this:
To find x in this ratio, just isolate x in the hypotenuse:
Divide by
Now, how does Quantity A and Quantity B match up?
On the surface, it looks like the two quanties are equal. But how do we prove it? Well, we know that 
Divide both sides by
Therefore, both quantities are equal.
← Didn't Know|Knew It →
We know that our area can be represented by the following equation:

Instead of solving the algebra, you should immediately note several things. 16 = 42 and 4 = 22. If the side of the square is 4, then s = 4 would work out as:

which is just what we need.
With s = 4, we know that 3 sides of our figure will have a perimeter of 12. The remaining semicircle will be one half of the circumference of a circle with diameter of 4; therefore it will be 0.5 * 4 * π or 2π.
Therefore, the outer perimeter of our figure is 12 + 2π.
We know that our area can be represented by the following equation:
Instead of solving the algebra, you should immediately note several things. 16 = 42 and 4 = 22. If the side of the square is 4, then s = 4 would work out as:
which is just what we need.
With s = 4, we know that 3 sides of our figure will have a perimeter of 12. The remaining semicircle will be one half of the circumference of a circle with diameter of 4; therefore it will be 0.5 * 4 * π or 2π.
Therefore, the outer perimeter of our figure is 12 + 2π.
← Didn't Know|Knew It →
What is the perimeter of a square that has an area of 81?
What is the perimeter of a square that has an area of 81?
Tap to reveal answer
36
A square has four equal sides and its area = side2. Therefore, you can find the side length by taking the square root of the area √81 = 9. Then, find the perimeter by multiplying the side length by 4:
4 * 9 = 36
36
A square has four equal sides and its area = side2. Therefore, you can find the side length by taking the square root of the area √81 = 9. Then, find the perimeter by multiplying the side length by 4:
4 * 9 = 36
← Didn't Know|Knew It →

The radius of the circle is 2 inches. What is the perimeter of the inscribed square?

The radius of the circle is 2 inches. What is the perimeter of the inscribed square?
Tap to reveal answer
The center of an inscribed square lies on the center of the circle. Thus, the line joining the center to a vertex of the square is also the radius. If we join the center with two adjacent vertices we can create a 45-45-90 right isosceles triangle, where the diagonal of the square is the hypotenuse. Since the radius is 2, the hypotenuse (a side of the square) must be  .
.
Finally, the perimeter of a square is  .
.
The center of an inscribed square lies on the center of the circle. Thus, the line joining the center to a vertex of the square is also the radius. If we join the center with two adjacent vertices we can create a 45-45-90 right isosceles triangle, where the diagonal of the square is the hypotenuse. Since the radius is 2, the hypotenuse (a side of the square) must be 
Finally, the perimeter of a square is 
← Didn't Know|Knew It →
A square table has an area of  square centimeters and a perimeter of
square centimeters and a perimeter of  centimeters.
centimeters.
If  , what is the perimeter of the square?
, what is the perimeter of the square?
A square table has an area of 

If 
Tap to reveal answer
We start by writing the equations for the area and perimeter in terms of a side of length s.


Then, substitute both of these expressions into the given equation to solve for side length.




Finally, since four sides make up the perimeter, we substitue s back into our perimeter equation and solve for P.

We start by writing the equations for the area and perimeter in terms of a side of length s.
Then, substitute both of these expressions into the given equation to solve for side length.
Finally, since four sides make up the perimeter, we substitue s back into our perimeter equation and solve for P.
← Didn't Know|Knew It →
The diagonal of square  is
is  feet. Approximately how long in inches is the perimeter of square
feet. Approximately how long in inches is the perimeter of square  ?
?
The diagonal of square 


Tap to reveal answer
First we must convert to inches.

The diagonal of a square divides the square into two isosceles-right triangles. Using the Pythagorean Theorem, we know that  , where x is equal to the length of one side of the square.
, where x is equal to the length of one side of the square.
This gives us  .
.
Therefore, the perimeter of square  is equal to
is equal to  .
.
First we must convert to inches.
The diagonal of a square divides the square into two isosceles-right triangles. Using the Pythagorean Theorem, we know that 
This gives us 
Therefore, the perimeter of square 

← Didn't Know|Knew It →
If a square has a side length of 4, how long is the diagonal of the square?
If a square has a side length of 4, how long is the diagonal of the square?
Tap to reveal answer
A diagonal divides a square into two 45-45-90 triangles, which have lengths adhering to the ratio of x: x: x√2. Therefore, 4√2 is the correct answer as the diagonal represents the hypotenuse of the triangle. the Pythagorean theorem can also be used: 42+ 42 = c2.
A diagonal divides a square into two 45-45-90 triangles, which have lengths adhering to the ratio of x: x: x√2. Therefore, 4√2 is the correct answer as the diagonal represents the hypotenuse of the triangle. the Pythagorean theorem can also be used: 42+ 42 = c2.
← Didn't Know|Knew It →
If a square has a side length of √2, how long is the diagonal of the square?
If a square has a side length of √2, how long is the diagonal of the square?
Tap to reveal answer
A diagonal divides a square into two 45-45-90 triangles, which have lengths adhering to the ratio of x: x: x√2. Therefore, 2 is the correct answer as the diagonal represents the hypotenuse of the triangle. the Pythagorean theorem can also be used: √22+ √22 = c2.
A diagonal divides a square into two 45-45-90 triangles, which have lengths adhering to the ratio of x: x: x√2. Therefore, 2 is the correct answer as the diagonal represents the hypotenuse of the triangle. the Pythagorean theorem can also be used: √22+ √22 = c2.
← Didn't Know|Knew It →
A square has a side of length 5. What is the length of its diagonal?
A square has a side of length 5. What is the length of its diagonal?
Tap to reveal answer
The diagonal separates the square into two 45-45-90 right triangles. The problem can be solved by using the Pythagorean Theorem, _a_2 + _b_2 = _c_2. It can also be solved by recognizing the 45-45-90 special triangles, which have side ratios of x : x : x√2.
The diagonal separates the square into two 45-45-90 right triangles. The problem can be solved by using the Pythagorean Theorem, _a_2 + _b_2 = _c_2. It can also be solved by recognizing the 45-45-90 special triangles, which have side ratios of x : x : x√2.
← Didn't Know|Knew It →
A square with width of  is inscribed in a circle. What is the total area inside the circle?
is inscribed in a circle. What is the total area inside the circle?
A square with width of 
Tap to reveal answer
We know that each side of the square is 6, so use the Pythagorean Theorem to solve for the diagonal of the square. The diagonal of the square is also the diameter of the circle.
$6^{2}$$+6^{2}$ = $d^{2}$
72= $d^{2}$
$\sqrt{72}$=d
$\sqrt{72}$=$\sqrt{36times 2}$=6$\sqrt{2}$
6$\sqrt{2}$=d
Therefore the radius must be r=\frac{6sqrt{2}$}{2}rightarrow 3$\sqrt{2}$
Now let's find the area inside the circle using the radius.
A=pi $r^{2}$
A=pileft (3$\sqrt{2}$ right $)^{2}$
A=pileft (3$\sqrt{2}$ right $)^{2}$rightarrow pileft ( 9times 2 right )rightarrow 18pi
A=18pi meters2
We know that each side of the square is 6, so use the Pythagorean Theorem to solve for the diagonal of the square. The diagonal of the square is also the diameter of the circle.
$6^{2}$$+6^{2}$ = $d^{2}$
72= $d^{2}$
$\sqrt{72}$=d
$\sqrt{72}$=$\sqrt{36times 2}$=6$\sqrt{2}$
6$\sqrt{2}$=d
Therefore the radius must be r=\frac{6sqrt{2}$}{2}rightarrow 3$\sqrt{2}$
Now let's find the area inside the circle using the radius.
A=pi $r^{2}$
A=pileft (3$\sqrt{2}$ right $)^{2}$
A=pileft (3$\sqrt{2}$ right $)^{2}$rightarrow pileft ( 9times 2 right )rightarrow 18pi
A=18pi meters2
← Didn't Know|Knew It →
Quantity A:
The diagonal of a square with a side-length of  .
.
Quantity B:
The side-length of a square with a diagonal of  .
.
Quantity A:
The diagonal of a square with a side-length of 
Quantity B:
The side-length of a square with a diagonal of 
Tap to reveal answer
Quantity A: The diagonal of a square with a side-length of 7.
Quantity B: The side-length of a square with a diagonal of 14.
Both quantities can be determined, so can the relationship.
Quantity A:
To determine the diagonal of a square, it's important to remember that a diagonal directly bisects a square from corner to corner. In other words, it bisects the corners, creating two triangles with 45:45:90 proportions, with the diagonal serving as the hypotenuses . If you remember your special triangles, then the side-side-hypotenuse measurements have a ratio of  .
.
In Quantity A, the side-length is 7. Following the proportion:

The diagonal equals  .
.
Quantity B:
We can use the same ratio to figure out quantity B by substituting x for the unknown side-length quantity, which looks like this:

To find x in this ratio, just isolate x in the hypotenuse:

Divide by 

Now, how does Quantity A and Quantity B match up?


On the surface, it looks like the two quanties are equal. But how do we prove it? Well, we know that  . Therefore, we know that:
. Therefore, we know that:

Divide both sides by 

Therefore, both quantities are equal.
Quantity A: The diagonal of a square with a side-length of 7.
Quantity B: The side-length of a square with a diagonal of 14.
Both quantities can be determined, so can the relationship.
Quantity A:
To determine the diagonal of a square, it's important to remember that a diagonal directly bisects a square from corner to corner. In other words, it bisects the corners, creating two triangles with 45:45:90 proportions, with the diagonal serving as the hypotenuses . If you remember your special triangles, then the side-side-hypotenuse measurements have a ratio of 
In Quantity A, the side-length is 7. Following the proportion:
The diagonal equals 
Quantity B:
We can use the same ratio to figure out quantity B by substituting x for the unknown side-length quantity, which looks like this:
To find x in this ratio, just isolate x in the hypotenuse:
Divide by
Now, how does Quantity A and Quantity B match up?
On the surface, it looks like the two quanties are equal. But how do we prove it? Well, we know that 
Divide both sides by
Therefore, both quantities are equal.
← Didn't Know|Knew It →
Find the area of a square with a side length of 4.
Find the area of a square with a side length of 4.
Tap to reveal answer
All sides are equal in a square. To find the area of a square, multiply length times width. We know length = 4 but since all sides are equal, the width is also 4. 4 * 4 = 16.
All sides are equal in a square. To find the area of a square, multiply length times width. We know length = 4 but since all sides are equal, the width is also 4. 4 * 4 = 16.
← Didn't Know|Knew It →
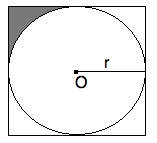
In order to solve this, we must first find the area of the containing square and then remove the inscribed circle. Once this is done, we need to divide our result by 4 in order to get the one-forth that is the one shaded region.
One side of the square will be equal to the circle's diameter (2r). Since r = 5, d = 10. Therefore, the area of the square is d2 = 102 = 100. The area of the circle is πr2 = 52π = 25π.
Therefore, the area of the four "corner regions" is equal to 100 - 25π. One of these is equal to (100 - 25π) / 4. Simplified, this is 25 - (25/4)π.
In order to solve this, we must first find the area of the containing square and then remove the inscribed circle. Once this is done, we need to divide our result by 4 in order to get the one-forth that is the one shaded region.
One side of the square will be equal to the circle's diameter (2r). Since r = 5, d = 10. Therefore, the area of the square is d2 = 102 = 100. The area of the circle is πr2 = 52π = 25π.
Therefore, the area of the four "corner regions" is equal to 100 - 25π. One of these is equal to (100 - 25π) / 4. Simplified, this is 25 - (25/4)π.
← Didn't Know|Knew It →
To compare, first calculate the area of figure 1. Since it shares dimensions with the semi-circle, we will put all our variables in terms of the radius of that semi-circle:
A1 = (2r)2 + πr2/2 = 4r2 + πr2/2 = r2(4 + π)/2
If we double r, we get:
A2 = (2 * 2r)2 + π(2r)2/2 = 16r2 + π4r2/2 = 4r2(4 + π)/2
This means that the new figure is 4x the size of the original. This is an increase of 300%.
To compare, first calculate the area of figure 1. Since it shares dimensions with the semi-circle, we will put all our variables in terms of the radius of that semi-circle:
A1 = (2r)2 + πr2/2 = 4r2 + πr2/2 = r2(4 + π)/2
If we double r, we get:
A2 = (2 * 2r)2 + π(2r)2/2 = 16r2 + π4r2/2 = 4r2(4 + π)/2
This means that the new figure is 4x the size of the original. This is an increase of 300%.
← Didn't Know|Knew It →
100 cm = 1 m
Quantity A: The area of a square with side 1 m
Quantity B: One hundred times the area of a square with side 1 cm
100 cm = 1 m
Quantity A: The area of a square with side 1 m
Quantity B: One hundred times the area of a square with side 1 cm
Tap to reveal answer
The obvious answer for this problem is that they are equal. Remember quantitative comparisons are often tricky and require you to check your initial inclination. If 1 m equals 100 cm then a square with side 1 m (100 cm) has an area of 100 cm x 100 cm or 10,000 cm2. The area of a square with a 1 cm side is 1 cm x 1 cm or 1 cm2. One hundred times 1 cm2 is 100 cm2. 10,000 cm2 is larger than 100 cm2 so Quantity A is greater.
The obvious answer for this problem is that they are equal. Remember quantitative comparisons are often tricky and require you to check your initial inclination. If 1 m equals 100 cm then a square with side 1 m (100 cm) has an area of 100 cm x 100 cm or 10,000 cm2. The area of a square with a 1 cm side is 1 cm x 1 cm or 1 cm2. One hundred times 1 cm2 is 100 cm2. 10,000 cm2 is larger than 100 cm2 so Quantity A is greater.
← Didn't Know|Knew It →
A square is inscribed in a circle. The diameter of the circle is 10 feet. What is the area of the square?
A square is inscribed in a circle. The diameter of the circle is 10 feet. What is the area of the square?
Tap to reveal answer
Since the diameter of the circle is 10, we know the radius of the circle is 5 feet. We can then draw radii that go from the center to two consecutive corners of the square. These radii are both 5 feet, and form a 90 degree angle (since they are diagonals of a square). Thus, with the enclosed side of the square they form a 45-45-90 triangle. Thus, the side of the square must be 5$\sqrt{2}$ (this can also be found with the Pythagorean theorem). Then, the area of the square is
5$\sqrt{2}$times $5$\sqrt{2}$=50ft^{2}$
Since the diameter of the circle is 10, we know the radius of the circle is 5 feet. We can then draw radii that go from the center to two consecutive corners of the square. These radii are both 5 feet, and form a 90 degree angle (since they are diagonals of a square). Thus, with the enclosed side of the square they form a 45-45-90 triangle. Thus, the side of the square must be 5$\sqrt{2}$ (this can also be found with the Pythagorean theorem). Then, the area of the square is
5$\sqrt{2}$times $5$\sqrt{2}$=50ft^{2}$
← Didn't Know|Knew It →