How to simplify square roots - GRE Quantitative Reasoning
Card 1 of 88
Simplify the following: (√(6) + √(3)) / √(3)
Simplify the following: (√(6) + √(3)) / √(3)
Tap to reveal answer
Begin by multiplying top and bottom by √(3):
(√(18) + √(9)) / 3
Note the following:
√(9) = 3
√(18) = √(9 * 2) = √(9) * √(2) = 3 * √(2)
Therefore, the numerator is: 3 * √(2) + 3. Factor out the common 3: 3 * (√(2) + 1)
Rewrite the whole fraction:
(3 * (√(2) + 1)) / 3
Simplfy by dividing cancelling the 3 common to numerator and denominator: √(2) + 1
Begin by multiplying top and bottom by √(3):
(√(18) + √(9)) / 3
Note the following:
√(9) = 3
√(18) = √(9 * 2) = √(9) * √(2) = 3 * √(2)
Therefore, the numerator is: 3 * √(2) + 3. Factor out the common 3: 3 * (√(2) + 1)
Rewrite the whole fraction:
(3 * (√(2) + 1)) / 3
Simplfy by dividing cancelling the 3 common to numerator and denominator: √(2) + 1
← Didn't Know|Knew It →
what is
√0.0000490
what is
√0.0000490
Tap to reveal answer
easiest way to simplify: turn into scientific notation
√0.0000490= √4.9 X 10-5
finding the square root of an even exponent is easy, and 49 is a perfect square, so we can write out an improper scientific notation:
√4.9 X 10-5 = √49 X 10-6
√49 = 7; √10-6 = 10-3 this is equivalent to raising 10-6 to the 1/2 power, in which case all that needs to be done is multiply the two exponents: 7 X 10-3= 0.007
easiest way to simplify: turn into scientific notation
√0.0000490= √4.9 X 10-5
finding the square root of an even exponent is easy, and 49 is a perfect square, so we can write out an improper scientific notation:
√4.9 X 10-5 = √49 X 10-6
√49 = 7; √10-6 = 10-3 this is equivalent to raising 10-6 to the 1/2 power, in which case all that needs to be done is multiply the two exponents: 7 X 10-3= 0.007
← Didn't Know|Knew It →
Which of the following is the most simplified form of:

Which of the following is the most simplified form of:
Tap to reveal answer
First find all of the prime factors of 

So 
First find all of the prime factors of
So
← Didn't Know|Knew It →
Which of the following is equal to  ?
?
Which of the following is equal to 
Tap to reveal answer
√75 can be broken down to √25 * √3. Which simplifies to 5√3.
√75 can be broken down to √25 * √3. Which simplifies to 5√3.
← Didn't Know|Knew It →
Simplify: 
Simplify:
Tap to reveal answer
In order to take the square root, divide 576 by 2.

In order to take the square root, divide 576 by 2.
← Didn't Know|Knew It →
Simplify $($\frac{16}{81}$)^{1/4}$.
Simplify $($\frac{16}{81}$)^{1/4}$.
Tap to reveal answer
$($\frac{16}{81}$)^{1/4}$
 $\frac{16^{1/4}$$$}{81^{1/4}$}
$\frac{16^{1/4}$$$}{81^{1/4}$}
 $\frac{(2cdot 2cdot 2cdot $2)^{1/4}$$}{(3cdot 3cdot 3cdot $3)^{1/4}$}
$\frac{(2cdot 2cdot 2cdot $2)^{1/4}$$}{(3cdot 3cdot 3cdot $3)^{1/4}$}
 $\frac{2}{3}$
$\frac{2}{3}$
$($\frac{16}{81}$)^{1/4}$



← Didn't Know|Knew It →
Simplify $$\sqrt{a^{3}$$$b^{4}$$c^{5}$}.
Simplify $$\sqrt{a^{3}$$$b^{4}$$c^{5}$}.
Tap to reveal answer
Rewrite what is under the radical in terms of perfect squares:
$x^{2}$=xcdot x
$x^{4}$$=x^{2}$cdot $x^{2}$
$x^{6}$$=x^{3}$cdot $x^{3}$
Therefore, $$\sqrt{a^{3}$$$b^{4}$$c^{5}$}= $$\sqrt{a^{2}$$$a^{1}$$b^{4}$$c^{4}$$c^{1}$$}=ab^{2}$$c^{2}$$\sqrt{ac}$.
Rewrite what is under the radical in terms of perfect squares:
$x^{2}$=xcdot x
$x^{4}$$=x^{2}$cdot $x^{2}$
$x^{6}$$=x^{3}$cdot $x^{3}$
Therefore, $$\sqrt{a^{3}$$$b^{4}$$c^{5}$}= $$\sqrt{a^{2}$$$a^{1}$$b^{4}$$c^{4}$$c^{1}$$}=ab^{2}$$c^{2}$$\sqrt{ac}$.
← Didn't Know|Knew It →
Which of the following is equivalent to $\frac{x + sqrt{3}$}{3x + $\sqrt{2}$}?
Which of the following is equivalent to $\frac{x + sqrt{3}$}{3x + $\sqrt{2}$}?
Tap to reveal answer
Multiply by the conjugate and the use the formula for the difference of two squares:
$\frac{x + sqrt{3}$}{3x + $\sqrt{2}$}
 $\frac{x + sqrt{3}$}{3x + $\sqrt{2}$}cdot $\frac{3x - sqrt{2}$}{3x - $\sqrt{2}$}
$\frac{x + sqrt{3}$}{3x + $\sqrt{2}$}cdot $\frac{3x - sqrt{2}$}{3x - $\sqrt{2}$}
 $$\frac{3x^{2}$$ -x $\sqrt{2}$ + 3x$\sqrt{3}$ - $$\sqrt{6}$}{(3x)^{2}$ - $($\sqrt{2}$)^{2}$}
$$\frac{3x^{2}$$ -x $\sqrt{2}$ + 3x$\sqrt{3}$ - $$\sqrt{6}$}{(3x)^{2}$ - $($\sqrt{2}$)^{2}$}
 $$\frac{3x^{2}$$ -x $\sqrt{2}$ + 3x$\sqrt{3}$ - $$\sqrt{6}$}{9x^{2}$ - 2}
$$\frac{3x^{2}$$ -x $\sqrt{2}$ + 3x$\sqrt{3}$ - $$\sqrt{6}$}{9x^{2}$ - 2}
Multiply by the conjugate and the use the formula for the difference of two squares:
$\frac{x + sqrt{3}$}{3x + $\sqrt{2}$}



← Didn't Know|Knew It →
What is  ?
?
What is 
Tap to reveal answer
We know that 25 is a factor of 50. The square root of 25 is 5. That leaves  which can not be simplified further.
which can not be simplified further.
We know that 25 is a factor of 50. The square root of 25 is 5. That leaves 
← Didn't Know|Knew It →
What is  equal to?
equal to?
What is 
Tap to reveal answer
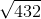
1. We know that  , which we can separate under the square root:
, which we can separate under the square root:

2. 144 can be taken out since it is a perfect square:  . This leaves us with:
. This leaves us with:

This cannot be simplified any further.
1. We know that 
2. 144 can be taken out since it is a perfect square: 
This cannot be simplified any further.
← Didn't Know|Knew It →
Simplfy the following radical  .
.
Simplfy the following radical 
Tap to reveal answer
You can rewrite the equation as  .
.
This simplifies to  .
.
You can rewrite the equation as 
This simplifies to 
← Didn't Know|Knew It →
Simplify the following: (√(6) + √(3)) / √(3)
Simplify the following: (√(6) + √(3)) / √(3)
Tap to reveal answer
Begin by multiplying top and bottom by √(3):
(√(18) + √(9)) / 3
Note the following:
√(9) = 3
√(18) = √(9 * 2) = √(9) * √(2) = 3 * √(2)
Therefore, the numerator is: 3 * √(2) + 3. Factor out the common 3: 3 * (√(2) + 1)
Rewrite the whole fraction:
(3 * (√(2) + 1)) / 3
Simplfy by dividing cancelling the 3 common to numerator and denominator: √(2) + 1
Begin by multiplying top and bottom by √(3):
(√(18) + √(9)) / 3
Note the following:
√(9) = 3
√(18) = √(9 * 2) = √(9) * √(2) = 3 * √(2)
Therefore, the numerator is: 3 * √(2) + 3. Factor out the common 3: 3 * (√(2) + 1)
Rewrite the whole fraction:
(3 * (√(2) + 1)) / 3
Simplfy by dividing cancelling the 3 common to numerator and denominator: √(2) + 1
← Didn't Know|Knew It →
what is
√0.0000490
what is
√0.0000490
Tap to reveal answer
easiest way to simplify: turn into scientific notation
√0.0000490= √4.9 X 10-5
finding the square root of an even exponent is easy, and 49 is a perfect square, so we can write out an improper scientific notation:
√4.9 X 10-5 = √49 X 10-6
√49 = 7; √10-6 = 10-3 this is equivalent to raising 10-6 to the 1/2 power, in which case all that needs to be done is multiply the two exponents: 7 X 10-3= 0.007
easiest way to simplify: turn into scientific notation
√0.0000490= √4.9 X 10-5
finding the square root of an even exponent is easy, and 49 is a perfect square, so we can write out an improper scientific notation:
√4.9 X 10-5 = √49 X 10-6
√49 = 7; √10-6 = 10-3 this is equivalent to raising 10-6 to the 1/2 power, in which case all that needs to be done is multiply the two exponents: 7 X 10-3= 0.007
← Didn't Know|Knew It →
Which of the following is the most simplified form of:

Which of the following is the most simplified form of:
Tap to reveal answer
First find all of the prime factors of 

So 
First find all of the prime factors of
So
← Didn't Know|Knew It →
Which of the following is equal to  ?
?
Which of the following is equal to 
Tap to reveal answer
√75 can be broken down to √25 * √3. Which simplifies to 5√3.
√75 can be broken down to √25 * √3. Which simplifies to 5√3.
← Didn't Know|Knew It →
Simplify: 
Simplify:
Tap to reveal answer
In order to take the square root, divide 576 by 2.

In order to take the square root, divide 576 by 2.
← Didn't Know|Knew It →
Simplify $($\frac{16}{81}$)^{1/4}$.
Simplify $($\frac{16}{81}$)^{1/4}$.
Tap to reveal answer
$($\frac{16}{81}$)^{1/4}$
 $\frac{16^{1/4}$$$}{81^{1/4}$}
$\frac{16^{1/4}$$$}{81^{1/4}$}
 $\frac{(2cdot 2cdot 2cdot $2)^{1/4}$$}{(3cdot 3cdot 3cdot $3)^{1/4}$}
$\frac{(2cdot 2cdot 2cdot $2)^{1/4}$$}{(3cdot 3cdot 3cdot $3)^{1/4}$}
 $\frac{2}{3}$
$\frac{2}{3}$
$($\frac{16}{81}$)^{1/4}$



← Didn't Know|Knew It →
Simplify $$\sqrt{a^{3}$$$b^{4}$$c^{5}$}.
Simplify $$\sqrt{a^{3}$$$b^{4}$$c^{5}$}.
Tap to reveal answer
Rewrite what is under the radical in terms of perfect squares:
$x^{2}$=xcdot x
$x^{4}$$=x^{2}$cdot $x^{2}$
$x^{6}$$=x^{3}$cdot $x^{3}$
Therefore, $$\sqrt{a^{3}$$$b^{4}$$c^{5}$}= $$\sqrt{a^{2}$$$a^{1}$$b^{4}$$c^{4}$$c^{1}$$}=ab^{2}$$c^{2}$$\sqrt{ac}$.
Rewrite what is under the radical in terms of perfect squares:
$x^{2}$=xcdot x
$x^{4}$$=x^{2}$cdot $x^{2}$
$x^{6}$$=x^{3}$cdot $x^{3}$
Therefore, $$\sqrt{a^{3}$$$b^{4}$$c^{5}$}= $$\sqrt{a^{2}$$$a^{1}$$b^{4}$$c^{4}$$c^{1}$$}=ab^{2}$$c^{2}$$\sqrt{ac}$.
← Didn't Know|Knew It →
Which of the following is equivalent to $\frac{x + sqrt{3}$}{3x + $\sqrt{2}$}?
Which of the following is equivalent to $\frac{x + sqrt{3}$}{3x + $\sqrt{2}$}?
Tap to reveal answer
Multiply by the conjugate and the use the formula for the difference of two squares:
$\frac{x + sqrt{3}$}{3x + $\sqrt{2}$}
 $\frac{x + sqrt{3}$}{3x + $\sqrt{2}$}cdot $\frac{3x - sqrt{2}$}{3x - $\sqrt{2}$}
$\frac{x + sqrt{3}$}{3x + $\sqrt{2}$}cdot $\frac{3x - sqrt{2}$}{3x - $\sqrt{2}$}
 $$\frac{3x^{2}$$ -x $\sqrt{2}$ + 3x$\sqrt{3}$ - $$\sqrt{6}$}{(3x)^{2}$ - $($\sqrt{2}$)^{2}$}
$$\frac{3x^{2}$$ -x $\sqrt{2}$ + 3x$\sqrt{3}$ - $$\sqrt{6}$}{(3x)^{2}$ - $($\sqrt{2}$)^{2}$}
 $$\frac{3x^{2}$$ -x $\sqrt{2}$ + 3x$\sqrt{3}$ - $$\sqrt{6}$}{9x^{2}$ - 2}
$$\frac{3x^{2}$$ -x $\sqrt{2}$ + 3x$\sqrt{3}$ - $$\sqrt{6}$}{9x^{2}$ - 2}
Multiply by the conjugate and the use the formula for the difference of two squares:
$\frac{x + sqrt{3}$}{3x + $\sqrt{2}$}



← Didn't Know|Knew It →
What is  ?
?
What is 
Tap to reveal answer
We know that 25 is a factor of 50. The square root of 25 is 5. That leaves  which can not be simplified further.
which can not be simplified further.
We know that 25 is a factor of 50. The square root of 25 is 5. That leaves 
← Didn't Know|Knew It →