How to find the area of a square - GRE Quantitative Reasoning
Card 1 of 56
Find the area of a square with a side length of 4.
Find the area of a square with a side length of 4.
Tap to reveal answer
All sides are equal in a square. To find the area of a square, multiply length times width. We know length = 4 but since all sides are equal, the width is also 4. 4 * 4 = 16.
All sides are equal in a square. To find the area of a square, multiply length times width. We know length = 4 but since all sides are equal, the width is also 4. 4 * 4 = 16.
← Didn't Know|Knew It →
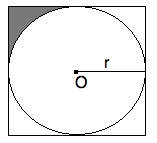
In order to solve this, we must first find the area of the containing square and then remove the inscribed circle. Once this is done, we need to divide our result by 4 in order to get the one-forth that is the one shaded region.
One side of the square will be equal to the circle's diameter (2r). Since r = 5, d = 10. Therefore, the area of the square is d2 = 102 = 100. The area of the circle is πr2 = 52π = 25π.
Therefore, the area of the four "corner regions" is equal to 100 - 25π. One of these is equal to (100 - 25π) / 4. Simplified, this is 25 - (25/4)π.
In order to solve this, we must first find the area of the containing square and then remove the inscribed circle. Once this is done, we need to divide our result by 4 in order to get the one-forth that is the one shaded region.
One side of the square will be equal to the circle's diameter (2r). Since r = 5, d = 10. Therefore, the area of the square is d2 = 102 = 100. The area of the circle is πr2 = 52π = 25π.
Therefore, the area of the four "corner regions" is equal to 100 - 25π. One of these is equal to (100 - 25π) / 4. Simplified, this is 25 - (25/4)π.
← Didn't Know|Knew It →
To compare, first calculate the area of figure 1. Since it shares dimensions with the semi-circle, we will put all our variables in terms of the radius of that semi-circle:
A1 = (2r)2 + πr2/2 = 4r2 + πr2/2 = r2(4 + π)/2
If we double r, we get:
A2 = (2 * 2r)2 + π(2r)2/2 = 16r2 + π4r2/2 = 4r2(4 + π)/2
This means that the new figure is 4x the size of the original. This is an increase of 300%.
To compare, first calculate the area of figure 1. Since it shares dimensions with the semi-circle, we will put all our variables in terms of the radius of that semi-circle:
A1 = (2r)2 + πr2/2 = 4r2 + πr2/2 = r2(4 + π)/2
If we double r, we get:
A2 = (2 * 2r)2 + π(2r)2/2 = 16r2 + π4r2/2 = 4r2(4 + π)/2
This means that the new figure is 4x the size of the original. This is an increase of 300%.
← Didn't Know|Knew It →
100 cm = 1 m
Quantity A: The area of a square with side 1 m
Quantity B: One hundred times the area of a square with side 1 cm
100 cm = 1 m
Quantity A: The area of a square with side 1 m
Quantity B: One hundred times the area of a square with side 1 cm
Tap to reveal answer
The obvious answer for this problem is that they are equal. Remember quantitative comparisons are often tricky and require you to check your initial inclination. If 1 m equals 100 cm then a square with side 1 m (100 cm) has an area of 100 cm x 100 cm or 10,000 cm2. The area of a square with a 1 cm side is 1 cm x 1 cm or 1 cm2. One hundred times 1 cm2 is 100 cm2. 10,000 cm2 is larger than 100 cm2 so Quantity A is greater.
The obvious answer for this problem is that they are equal. Remember quantitative comparisons are often tricky and require you to check your initial inclination. If 1 m equals 100 cm then a square with side 1 m (100 cm) has an area of 100 cm x 100 cm or 10,000 cm2. The area of a square with a 1 cm side is 1 cm x 1 cm or 1 cm2. One hundred times 1 cm2 is 100 cm2. 10,000 cm2 is larger than 100 cm2 so Quantity A is greater.
← Didn't Know|Knew It →
A square is inscribed in a circle. The diameter of the circle is 10 feet. What is the area of the square?
A square is inscribed in a circle. The diameter of the circle is 10 feet. What is the area of the square?
Tap to reveal answer
Since the diameter of the circle is 10, we know the radius of the circle is 5 feet. We can then draw radii that go from the center to two consecutive corners of the square. These radii are both 5 feet, and form a 90 degree angle (since they are diagonals of a square). Thus, with the enclosed side of the square they form a 45-45-90 triangle. Thus, the side of the square must be 5$\sqrt{2}$ (this can also be found with the Pythagorean theorem). Then, the area of the square is
5$\sqrt{2}$times $5$\sqrt{2}$=50ft^{2}$
Since the diameter of the circle is 10, we know the radius of the circle is 5 feet. We can then draw radii that go from the center to two consecutive corners of the square. These radii are both 5 feet, and form a 90 degree angle (since they are diagonals of a square). Thus, with the enclosed side of the square they form a 45-45-90 triangle. Thus, the side of the square must be 5$\sqrt{2}$ (this can also be found with the Pythagorean theorem). Then, the area of the square is
5$\sqrt{2}$times $5$\sqrt{2}$=50ft^{2}$
← Didn't Know|Knew It →

In the figure above, a square is inscribed in a circle with a diameter of 5 cm.
What is the area of the square?

In the figure above, a square is inscribed in a circle with a diameter of 5 cm.
What is the area of the square?
Tap to reveal answer
The diameter of the circle and the sides of the square form a 45-45-90 triangle. Since the hypotenuse is 5 cm, then a leg of the triangle (a side of the square) is  .
.
The area of the square is then  .
.
The diameter of the circle and the sides of the square form a 45-45-90 triangle. Since the hypotenuse is 5 cm, then a leg of the triangle (a side of the square) is 
The area of the square is then 
← Didn't Know|Knew It →
Square  is on a coordinate plane, and each side of the square is parallel to either the
is on a coordinate plane, and each side of the square is parallel to either the  -axis or
-axis or  -axis. Point
-axis. Point  has the coordinate
has the coordinate  and Point
and Point  has the coordinate
has the coordinate 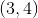 .
.
Quantity A: The area of square 
Quantity B: 24
Square 





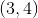
Quantity A: The area of square
Quantity B: 24
Tap to reveal answer
If you draw points  and
and  on the coordinate plane, you know that they are opposite ends of the square, since the sides are parallel to the axes. This means that the squares have sides with lengths of 5, making the area 25.
on the coordinate plane, you know that they are opposite ends of the square, since the sides are parallel to the axes. This means that the squares have sides with lengths of 5, making the area 25.
If you draw points 

← Didn't Know|Knew It →
To compare, first calculate the area of figure 1. Since it shares dimensions with the semi-circle, we will put all our variables in terms of the radius of that semi-circle:
A1 = (2r)2 + πr2/2 = 4r2 + πr2/2 = r2(4 + π)/2
If we double r, we get:
A2 = (2 * 2r)2 + π(2r)2/2 = 16r2 + π4r2/2 = 4r2(4 + π)/2
This means that the new figure is 4x the size of the original. This is an increase of 300%.
To compare, first calculate the area of figure 1. Since it shares dimensions with the semi-circle, we will put all our variables in terms of the radius of that semi-circle:
A1 = (2r)2 + πr2/2 = 4r2 + πr2/2 = r2(4 + π)/2
If we double r, we get:
A2 = (2 * 2r)2 + π(2r)2/2 = 16r2 + π4r2/2 = 4r2(4 + π)/2
This means that the new figure is 4x the size of the original. This is an increase of 300%.
← Didn't Know|Knew It →
100 cm = 1 m
Quantity A: The area of a square with side 1 m
Quantity B: One hundred times the area of a square with side 1 cm
100 cm = 1 m
Quantity A: The area of a square with side 1 m
Quantity B: One hundred times the area of a square with side 1 cm
Tap to reveal answer
The obvious answer for this problem is that they are equal. Remember quantitative comparisons are often tricky and require you to check your initial inclination. If 1 m equals 100 cm then a square with side 1 m (100 cm) has an area of 100 cm x 100 cm or 10,000 cm2. The area of a square with a 1 cm side is 1 cm x 1 cm or 1 cm2. One hundred times 1 cm2 is 100 cm2. 10,000 cm2 is larger than 100 cm2 so Quantity A is greater.
The obvious answer for this problem is that they are equal. Remember quantitative comparisons are often tricky and require you to check your initial inclination. If 1 m equals 100 cm then a square with side 1 m (100 cm) has an area of 100 cm x 100 cm or 10,000 cm2. The area of a square with a 1 cm side is 1 cm x 1 cm or 1 cm2. One hundred times 1 cm2 is 100 cm2. 10,000 cm2 is larger than 100 cm2 so Quantity A is greater.
← Didn't Know|Knew It →
In order to solve this, we must first find the area of the containing square and then remove the inscribed circle. Once this is done, we need to divide our result by 4 in order to get the one-forth that is the one shaded region.
One side of the square will be equal to the circle's diameter (2r). Since r = 5, d = 10. Therefore, the area of the square is d2 = 102 = 100. The area of the circle is πr2 = 52π = 25π.
Therefore, the area of the four "corner regions" is equal to 100 - 25π. One of these is equal to (100 - 25π) / 4. Simplified, this is 25 - (25/4)π.
In order to solve this, we must first find the area of the containing square and then remove the inscribed circle. Once this is done, we need to divide our result by 4 in order to get the one-forth that is the one shaded region.
One side of the square will be equal to the circle's diameter (2r). Since r = 5, d = 10. Therefore, the area of the square is d2 = 102 = 100. The area of the circle is πr2 = 52π = 25π.
Therefore, the area of the four "corner regions" is equal to 100 - 25π. One of these is equal to (100 - 25π) / 4. Simplified, this is 25 - (25/4)π.
← Didn't Know|Knew It →
Find the area of a square with a side length of 4.
Find the area of a square with a side length of 4.
Tap to reveal answer
All sides are equal in a square. To find the area of a square, multiply length times width. We know length = 4 but since all sides are equal, the width is also 4. 4 * 4 = 16.
All sides are equal in a square. To find the area of a square, multiply length times width. We know length = 4 but since all sides are equal, the width is also 4. 4 * 4 = 16.
← Didn't Know|Knew It →
A square is inscribed in a circle. The diameter of the circle is 10 feet. What is the area of the square?
A square is inscribed in a circle. The diameter of the circle is 10 feet. What is the area of the square?
Tap to reveal answer
Since the diameter of the circle is 10, we know the radius of the circle is 5 feet. We can then draw radii that go from the center to two consecutive corners of the square. These radii are both 5 feet, and form a 90 degree angle (since they are diagonals of a square). Thus, with the enclosed side of the square they form a 45-45-90 triangle. Thus, the side of the square must be 5$\sqrt{2}$ (this can also be found with the Pythagorean theorem). Then, the area of the square is
5$\sqrt{2}$times $5$\sqrt{2}$=50ft^{2}$
Since the diameter of the circle is 10, we know the radius of the circle is 5 feet. We can then draw radii that go from the center to two consecutive corners of the square. These radii are both 5 feet, and form a 90 degree angle (since they are diagonals of a square). Thus, with the enclosed side of the square they form a 45-45-90 triangle. Thus, the side of the square must be 5$\sqrt{2}$ (this can also be found with the Pythagorean theorem). Then, the area of the square is
5$\sqrt{2}$times $5$\sqrt{2}$=50ft^{2}$
← Didn't Know|Knew It →

In the figure above, a square is inscribed in a circle with a diameter of 5 cm.
What is the area of the square?

In the figure above, a square is inscribed in a circle with a diameter of 5 cm.
What is the area of the square?
Tap to reveal answer
The diameter of the circle and the sides of the square form a 45-45-90 triangle. Since the hypotenuse is 5 cm, then a leg of the triangle (a side of the square) is  .
.
The area of the square is then  .
.
The diameter of the circle and the sides of the square form a 45-45-90 triangle. Since the hypotenuse is 5 cm, then a leg of the triangle (a side of the square) is 
The area of the square is then 
← Didn't Know|Knew It →
Square  is on a coordinate plane, and each side of the square is parallel to either the
is on a coordinate plane, and each side of the square is parallel to either the  -axis or
-axis or  -axis. Point
-axis. Point  has the coordinate
has the coordinate  and Point
and Point  has the coordinate
has the coordinate 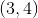 .
.
Quantity A: The area of square 
Quantity B: 24
Square 





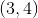
Quantity A: The area of square
Quantity B: 24
Tap to reveal answer
If you draw points  and
and  on the coordinate plane, you know that they are opposite ends of the square, since the sides are parallel to the axes. This means that the squares have sides with lengths of 5, making the area 25.
on the coordinate plane, you know that they are opposite ends of the square, since the sides are parallel to the axes. This means that the squares have sides with lengths of 5, making the area 25.
If you draw points 

← Didn't Know|Knew It →
Find the area of a square with a side length of 4.
Find the area of a square with a side length of 4.
Tap to reveal answer
All sides are equal in a square. To find the area of a square, multiply length times width. We know length = 4 but since all sides are equal, the width is also 4. 4 * 4 = 16.
All sides are equal in a square. To find the area of a square, multiply length times width. We know length = 4 but since all sides are equal, the width is also 4. 4 * 4 = 16.
← Didn't Know|Knew It →
In order to solve this, we must first find the area of the containing square and then remove the inscribed circle. Once this is done, we need to divide our result by 4 in order to get the one-forth that is the one shaded region.
One side of the square will be equal to the circle's diameter (2r). Since r = 5, d = 10. Therefore, the area of the square is d2 = 102 = 100. The area of the circle is πr2 = 52π = 25π.
Therefore, the area of the four "corner regions" is equal to 100 - 25π. One of these is equal to (100 - 25π) / 4. Simplified, this is 25 - (25/4)π.
In order to solve this, we must first find the area of the containing square and then remove the inscribed circle. Once this is done, we need to divide our result by 4 in order to get the one-forth that is the one shaded region.
One side of the square will be equal to the circle's diameter (2r). Since r = 5, d = 10. Therefore, the area of the square is d2 = 102 = 100. The area of the circle is πr2 = 52π = 25π.
Therefore, the area of the four "corner regions" is equal to 100 - 25π. One of these is equal to (100 - 25π) / 4. Simplified, this is 25 - (25/4)π.
← Didn't Know|Knew It →
To compare, first calculate the area of figure 1. Since it shares dimensions with the semi-circle, we will put all our variables in terms of the radius of that semi-circle:
A1 = (2r)2 + πr2/2 = 4r2 + πr2/2 = r2(4 + π)/2
If we double r, we get:
A2 = (2 * 2r)2 + π(2r)2/2 = 16r2 + π4r2/2 = 4r2(4 + π)/2
This means that the new figure is 4x the size of the original. This is an increase of 300%.
To compare, first calculate the area of figure 1. Since it shares dimensions with the semi-circle, we will put all our variables in terms of the radius of that semi-circle:
A1 = (2r)2 + πr2/2 = 4r2 + πr2/2 = r2(4 + π)/2
If we double r, we get:
A2 = (2 * 2r)2 + π(2r)2/2 = 16r2 + π4r2/2 = 4r2(4 + π)/2
This means that the new figure is 4x the size of the original. This is an increase of 300%.
← Didn't Know|Knew It →
100 cm = 1 m
Quantity A: The area of a square with side 1 m
Quantity B: One hundred times the area of a square with side 1 cm
100 cm = 1 m
Quantity A: The area of a square with side 1 m
Quantity B: One hundred times the area of a square with side 1 cm
Tap to reveal answer
The obvious answer for this problem is that they are equal. Remember quantitative comparisons are often tricky and require you to check your initial inclination. If 1 m equals 100 cm then a square with side 1 m (100 cm) has an area of 100 cm x 100 cm or 10,000 cm2. The area of a square with a 1 cm side is 1 cm x 1 cm or 1 cm2. One hundred times 1 cm2 is 100 cm2. 10,000 cm2 is larger than 100 cm2 so Quantity A is greater.
The obvious answer for this problem is that they are equal. Remember quantitative comparisons are often tricky and require you to check your initial inclination. If 1 m equals 100 cm then a square with side 1 m (100 cm) has an area of 100 cm x 100 cm or 10,000 cm2. The area of a square with a 1 cm side is 1 cm x 1 cm or 1 cm2. One hundred times 1 cm2 is 100 cm2. 10,000 cm2 is larger than 100 cm2 so Quantity A is greater.
← Didn't Know|Knew It →
A square is inscribed in a circle. The diameter of the circle is 10 feet. What is the area of the square?
A square is inscribed in a circle. The diameter of the circle is 10 feet. What is the area of the square?
Tap to reveal answer
Since the diameter of the circle is 10, we know the radius of the circle is 5 feet. We can then draw radii that go from the center to two consecutive corners of the square. These radii are both 5 feet, and form a 90 degree angle (since they are diagonals of a square). Thus, with the enclosed side of the square they form a 45-45-90 triangle. Thus, the side of the square must be 5$\sqrt{2}$ (this can also be found with the Pythagorean theorem). Then, the area of the square is
5$\sqrt{2}$times $5$\sqrt{2}$=50ft^{2}$
Since the diameter of the circle is 10, we know the radius of the circle is 5 feet. We can then draw radii that go from the center to two consecutive corners of the square. These radii are both 5 feet, and form a 90 degree angle (since they are diagonals of a square). Thus, with the enclosed side of the square they form a 45-45-90 triangle. Thus, the side of the square must be 5$\sqrt{2}$ (this can also be found with the Pythagorean theorem). Then, the area of the square is
5$\sqrt{2}$times $5$\sqrt{2}$=50ft^{2}$
← Didn't Know|Knew It →

In the figure above, a square is inscribed in a circle with a diameter of 5 cm.
What is the area of the square?

In the figure above, a square is inscribed in a circle with a diameter of 5 cm.
What is the area of the square?
Tap to reveal answer
The diameter of the circle and the sides of the square form a 45-45-90 triangle. Since the hypotenuse is 5 cm, then a leg of the triangle (a side of the square) is  .
.
The area of the square is then  .
.
The diameter of the circle and the sides of the square form a 45-45-90 triangle. Since the hypotenuse is 5 cm, then a leg of the triangle (a side of the square) is 
The area of the square is then 
← Didn't Know|Knew It →