Data Analysis - GRE Quantitative Reasoning
Card 1 of 1128
The medians of the following two sets of numbers are equal, and
the sets are arranged in ascending order
{1, 4, x, 8} and {2, 5, y, 9}. What is y – x?
The medians of the following two sets of numbers are equal, and
the sets are arranged in ascending order
{1, 4, x, 8} and {2, 5, y, 9}. What is y – x?
Tap to reveal answer
Answer: –1
Explanation: Recall that the median of an even-numbered set of numbers is the arithmetic mean of the pair of middle terms. Thus (4 + x)/2 = median of the first set and (5 + y)/2 = median of the second set. Since both medians are equal, we can set the equations equal to eachother. (4 + x)/2 = (5 + y)/2. Multiply both sides by 2 and we get 4 + x = 5 + y. We also know that 4 < x < 8 and 5 < y < 9, since the sets are arranged in ascending order. This narrows our options for x and y down significantly. Plugging in various values will eventually get you to x = 7 and y = 6, since 7 + 4 = 11 and 5 + 6 = 11, and thus the median in both cases would be 5.5. Thus, y – x = –1.
Answer: –1
Explanation: Recall that the median of an even-numbered set of numbers is the arithmetic mean of the pair of middle terms. Thus (4 + x)/2 = median of the first set and (5 + y)/2 = median of the second set. Since both medians are equal, we can set the equations equal to eachother. (4 + x)/2 = (5 + y)/2. Multiply both sides by 2 and we get 4 + x = 5 + y. We also know that 4 < x < 8 and 5 < y < 9, since the sets are arranged in ascending order. This narrows our options for x and y down significantly. Plugging in various values will eventually get you to x = 7 and y = 6, since 7 + 4 = 11 and 5 + 6 = 11, and thus the median in both cases would be 5.5. Thus, y – x = –1.
← Didn't Know|Knew It →
There are 3,500 people in group A and 5,000 people in group B:
Car Type % in Group A Who Own % in Group B Who Own Motorbike 4 9 Sedan 35 25 Minivan 22 15 Van 9 12 Coupe 3 6
What is the median of the number of people in group B who own either a minivan, van, or coupe?
There are 3,500 people in group A and 5,000 people in group B:
| Car Type | % in Group A Who Own | % in Group B Who Own |
|---|---|---|
| Motorbike | 4 | 9 |
| Sedan | 35 | 25 |
| Minivan | 22 | 15 |
| Van | 9 | 12 |
| Coupe | 3 | 6 |
What is the median of the number of people in group B who own either a minivan, van, or coupe?
Tap to reveal answer
Treat the percentages as a list, as we are including every demographic from the 3 vehicle types mentioned. If we do each 0.06(5000), 0.12(5000), and 0.15(5000) we note from observation that the median, or middle value, would have to be the 12% row since the sample size does not change. The question asks for EITHER of the 3 categories, so we can ignore the other two.
0.12(5000) = 600(van) is the median of the 3 categories.
Treat the percentages as a list, as we are including every demographic from the 3 vehicle types mentioned. If we do each 0.06(5000), 0.12(5000), and 0.15(5000) we note from observation that the median, or middle value, would have to be the 12% row since the sample size does not change. The question asks for EITHER of the 3 categories, so we can ignore the other two.
0.12(5000) = 600(van) is the median of the 3 categories.
← Didn't Know|Knew It →
Find the median:

Find the median:
Tap to reveal answer
To find the median, arrange the numbers from smallest to largest:
4,4,4,4,6,7,9,9,12,12,12,12,12,12,18,76,90
There are 17 numbers in total. Since 17 is an odd number, the median will be the middle number of the set. In this case, it is the 9th number, which is 12.
To find the median, arrange the numbers from smallest to largest:
4,4,4,4,6,7,9,9,12,12,12,12,12,12,18,76,90
There are 17 numbers in total. Since 17 is an odd number, the median will be the middle number of the set. In this case, it is the 9th number, which is 12.
← Didn't Know|Knew It →
What is the median in the following set of numbers?
16, 19, 16, 7, 2, 20, 9, 5
What is the median in the following set of numbers?
16, 19, 16, 7, 2, 20, 9, 5
Tap to reveal answer
16, 19, 16, 7, 2, 20, 9, 5
Order the numbers from smallest to largest.
2,5,7,9,16,16,19,20
The median is the number in the middle.
In this case, there is a 9 and 16 in the middle.
When that happens, take the average of the two numbers.
16, 19, 16, 7, 2, 20, 9, 5
Order the numbers from smallest to largest.
2,5,7,9,16,16,19,20
The median is the number in the middle.
In this case, there is a 9 and 16 in the middle.
When that happens, take the average of the two numbers.
← Didn't Know|Knew It →

In the set above, which is larger: the median, the mean, or the mode?
In the set above, which is larger: the median, the mean, or the mode?
Tap to reveal answer
Begin by ordering the set from smallest to largest:

Already, we see that the mode is 8. Find the median by taking the average of the two middle numbers:

Find the mean by adding all numbers and dividing by the total number of terms:

Of the three, the mean of the set is the largest.
Begin by ordering the set from smallest to largest:
Already, we see that the mode is 8. Find the median by taking the average of the two middle numbers:
Find the mean by adding all numbers and dividing by the total number of terms:
Of the three, the mean of the set is the largest.
← Didn't Know|Knew It →
The grades on a test taken by  students are
students are  respectively. What was the median score for this test?
respectively. What was the median score for this test?
The grades on a test taken by 

Tap to reveal answer
To solve this problem, we must be aware of the definition of a median for a set of numbers. The median is defined as the number that is in middle of a set of numbers sorted from smallest to largest. Therefore we must first sort the numbers from largest to smallest.
34,43,45,50,56,65,70,76,76,82,87,88,92,95,100
43,45,50,56,65,70,76,76,81,87,88,82,95
45,50,56,65,70,76,76,81,87,88,82
50,56,65,70,76,76,81,87,88
56,65,70,76,76,81,87
65,70,76,76,81
70,76,76
76
Then by slowly eliminating the smallest and the largest numbers we find that the median score for this test is 76.
To solve this problem, we must be aware of the definition of a median for a set of numbers. The median is defined as the number that is in middle of a set of numbers sorted from smallest to largest. Therefore we must first sort the numbers from largest to smallest.
34,43,45,50,56,65,70,76,76,82,87,88,92,95,100
43,45,50,56,65,70,76,76,81,87,88,82,95
45,50,56,65,70,76,76,81,87,88,82
50,56,65,70,76,76,81,87,88
56,65,70,76,76,81,87
65,70,76,76,81
70,76,76
76
Then by slowly eliminating the smallest and the largest numbers we find that the median score for this test is 76.
← Didn't Know|Knew It →
The arithmetic mean of  is
is 

 The median of
The median of 
The arithmetic mean of 

Tap to reveal answer
 is an unknown value, but it can be found given what we know about the mean of the set
is an unknown value, but it can be found given what we know about the mean of the set  :
:






Now,  is out of order; arrange in numerically:
is out of order; arrange in numerically:

Since there are even number of values, the median is the mean of the two middle most values:




Now, 
Since there are even number of values, the median is the mean of the two middle most values:
← Didn't Know|Knew It →
![Set_A=[-10,4,2,-14,-2]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/488996/gif.latex)
Quantity A: The mean of 
Quantity B: The median of 
Quantity A: The mean of
Quantity B: The median of
Tap to reveal answer
Begin by reordering the set in numerical order:
![Set_A=[-10,4,2,-14,-2]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/488997/gif.latex)
Then becomes
![Set_A=[-14,-10,-2,2,4]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/488998/gif.latex)
Since there is an odd number of values, the median is the middle value.
Quantity B: 
Now, to find the arithmetic mean, take the sum of values divided by the total number of values.

Quantity A: 
Begin by reordering the set in numerical order:
Then becomes
Since there is an odd number of values, the median is the middle value.
Quantity B:
Now, to find the arithmetic mean, take the sum of values divided by the total number of values.
Quantity A:
← Didn't Know|Knew It →
A given company has 1500 employees. Of those employees, 800 are computer science majors. 25% of those computer science majors are also mathematics majors. That group of computer science/math dual majors makes up one third of the total mathematics majors. How many employees have majors other than computer science and mathematics?
A given company has 1500 employees. Of those employees, 800 are computer science majors. 25% of those computer science majors are also mathematics majors. That group of computer science/math dual majors makes up one third of the total mathematics majors. How many employees have majors other than computer science and mathematics?
Tap to reveal answer
Refer to the following Venn Diagram:
If 25% of the 800 CS students are also mathematics students, the number of students sharing these majors is 800 * 0.25 or 200 students. Furthermore, if this represents one third of the total of math students, we then know:
Math students * 1/3 = 200 or (1/3)M = 200
Solving for M we get 600. This means that the number of students that are ONLY math students is 400.
Looking at our diagram above, we must be careful not to "double add" the intersection. The easiest way to do this is to take the intersection and add to it the number of CS-only and math-only students: 600 + 200 + 400 = 1200. This number represents the total number of students that have either a math or CS major (that is, the number of students in the union of the two sets). This leaves 1500 – 1200 or 300 students.
Refer to the following Venn Diagram:
If 25% of the 800 CS students are also mathematics students, the number of students sharing these majors is 800 * 0.25 or 200 students. Furthermore, if this represents one third of the total of math students, we then know:
Math students * 1/3 = 200 or (1/3)M = 200
Solving for M we get 600. This means that the number of students that are ONLY math students is 400.
Looking at our diagram above, we must be careful not to "double add" the intersection. The easiest way to do this is to take the intersection and add to it the number of CS-only and math-only students: 600 + 200 + 400 = 1200. This number represents the total number of students that have either a math or CS major (that is, the number of students in the union of the two sets). This leaves 1500 – 1200 or 300 students.
← Didn't Know|Knew It →
In a class, there are 15 students who like chocolate. 13 students like vanilla. 10 students like neither. If there are 35 people in the class, how many students like chocolate and vanilla?
In a class, there are 15 students who like chocolate. 13 students like vanilla. 10 students like neither. If there are 35 people in the class, how many students like chocolate and vanilla?
Tap to reveal answer
In order to find the intersection of chocolate and vanilla, it is easiest to make a Venn Diagram. The outside of the Venn Diagram is 10, and the total of the entire diagram must equal 35. Therefore the two circles of the Venn Diagram including just chocolate, just vanilla and the intersection must equal 25, with the just chocolate plus intersection side equalling 15 and the just vanilla plus intersection side equalling 13.
We know:
(A U B) = A + B – (A ∩ B)
We have found that (A U B) = 25 and we are trying to find (A ∩ B). Plug in A and B
25 = 15 + 13 – (A ∩ B) = 28 – (A ∩ B)
or – (A ∩ B) = –3
(A ∩ B) = 3
In order to find the intersection of chocolate and vanilla, it is easiest to make a Venn Diagram. The outside of the Venn Diagram is 10, and the total of the entire diagram must equal 35. Therefore the two circles of the Venn Diagram including just chocolate, just vanilla and the intersection must equal 25, with the just chocolate plus intersection side equalling 15 and the just vanilla plus intersection side equalling 13.
We know:
(A U B) = A + B – (A ∩ B)
We have found that (A U B) = 25 and we are trying to find (A ∩ B). Plug in A and B
25 = 15 + 13 – (A ∩ B) = 28 – (A ∩ B)
or – (A ∩ B) = –3
(A ∩ B) = 3
← Didn't Know|Knew It →
In a population of cats, 10% are tabby colored, 5% are pregnant, and 3% are both tabby and pregnant. What is the probability that a cat is tabby but not pregnant?
In a population of cats, 10% are tabby colored, 5% are pregnant, and 3% are both tabby and pregnant. What is the probability that a cat is tabby but not pregnant?
Tap to reveal answer
Probability (tabby but not pregnant)
= Prob (tabby) – Prob (tabby and pregnant)
= 10% - 3%
= 7%
Probability (tabby but not pregnant)
= Prob (tabby) – Prob (tabby and pregnant)
= 10% - 3%
= 7%
← Didn't Know|Knew It →
At an overpriced department store there are  customers. If
customers. If  have purchased shirts,
have purchased shirts,  have purchased pants, and
have purchased pants, and  have purchased neither, how many purchased both shirts and pants?
have purchased neither, how many purchased both shirts and pants?
At an overpriced department store there are 



Tap to reveal answer
A way of solving this problem is by drawing a Venn diagram based on what is known:
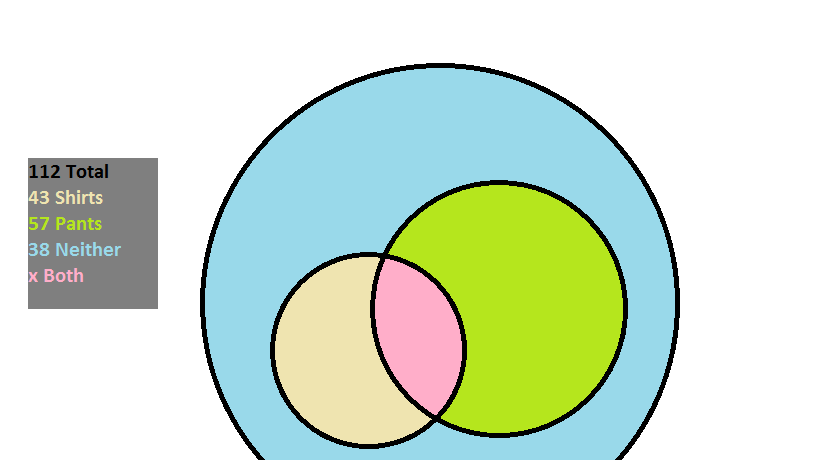
There are  customers; within them there are those that purchased something (pants, shirts, or possibly a combination), and those that purchased nothing.
customers; within them there are those that purchased something (pants, shirts, or possibly a combination), and those that purchased nothing.
The amount of individuals that purchased something is given as:

The reason that the number of shoppers that bought both is subtracted is so that it is not counted twice when the customers that bought pants and the customers that bought shirts are added together.
Since  bought nothing,
bought nothing,

The amount that bought both then is:


A way of solving this problem is by drawing a Venn diagram based on what is known:

There are 
The amount of individuals that purchased something is given as:
The reason that the number of shoppers that bought both is subtracted is so that it is not counted twice when the customers that bought pants and the customers that bought shirts are added together.
Since 
The amount that bought both then is:
← Didn't Know|Knew It →
In a school, 70 students are taking classes. 35 of them will be taking Accounting and 20 of them will be taking Economics. 7 of them are taking both of these classes. How many of the students are not in either class?
In a school, 70 students are taking classes. 35 of them will be taking Accounting and 20 of them will be taking Economics. 7 of them are taking both of these classes. How many of the students are not in either class?
Tap to reveal answer
When you add both class rosters you get a total of 55 students
 .
.
You must subtract the 7 that are in both because they are counted twice in the 55
 .
.
The total in neither class will be the total students minus the adjusted enrollment in both classes
 .
.
When you add both class rosters you get a total of 55 students

You must subtract the 7 that are in both because they are counted twice in the 55

The total in neither class will be the total students minus the adjusted enrollment in both classes

← Didn't Know|Knew It →
A given company has 1500 employees. Of those employees, 800 are computer science majors. 25% of those computer science majors are also mathematics majors. That group of computer science/math dual majors makes up one third of the total mathematics majors. How many employees have majors other than computer science and mathematics?
A given company has 1500 employees. Of those employees, 800 are computer science majors. 25% of those computer science majors are also mathematics majors. That group of computer science/math dual majors makes up one third of the total mathematics majors. How many employees have majors other than computer science and mathematics?
Tap to reveal answer
Refer to the following Venn Diagram:
If 25% of the 800 CS students are also mathematics students, the number of students sharing these majors is 800 * 0.25 or 200 students. Furthermore, if this represents one third of the total of math students, we then know:
Math students * 1/3 = 200 or (1/3)M = 200
Solving for M we get 600. This means that the number of students that are ONLY math students is 400.
Looking at our diagram above, we must be careful not to "double add" the intersection. The easiest way to do this is to take the intersection and add to it the number of CS-only and math-only students: 600 + 200 + 400 = 1200. This number represents the total number of students that have either a math or CS major (that is, the number of students in the union of the two sets). This leaves 1500 – 1200 or 300 students.
Refer to the following Venn Diagram:
If 25% of the 800 CS students are also mathematics students, the number of students sharing these majors is 800 * 0.25 or 200 students. Furthermore, if this represents one third of the total of math students, we then know:
Math students * 1/3 = 200 or (1/3)M = 200
Solving for M we get 600. This means that the number of students that are ONLY math students is 400.
Looking at our diagram above, we must be careful not to "double add" the intersection. The easiest way to do this is to take the intersection and add to it the number of CS-only and math-only students: 600 + 200 + 400 = 1200. This number represents the total number of students that have either a math or CS major (that is, the number of students in the union of the two sets). This leaves 1500 – 1200 or 300 students.
← Didn't Know|Knew It →
In a class, there are 15 students who like chocolate. 13 students like vanilla. 10 students like neither. If there are 35 people in the class, how many students like chocolate and vanilla?
In a class, there are 15 students who like chocolate. 13 students like vanilla. 10 students like neither. If there are 35 people in the class, how many students like chocolate and vanilla?
Tap to reveal answer
In order to find the intersection of chocolate and vanilla, it is easiest to make a Venn Diagram. The outside of the Venn Diagram is 10, and the total of the entire diagram must equal 35. Therefore the two circles of the Venn Diagram including just chocolate, just vanilla and the intersection must equal 25, with the just chocolate plus intersection side equalling 15 and the just vanilla plus intersection side equalling 13.
We know:
(A U B) = A + B – (A ∩ B)
We have found that (A U B) = 25 and we are trying to find (A ∩ B). Plug in A and B
25 = 15 + 13 – (A ∩ B) = 28 – (A ∩ B)
or – (A ∩ B) = –3
(A ∩ B) = 3
In order to find the intersection of chocolate and vanilla, it is easiest to make a Venn Diagram. The outside of the Venn Diagram is 10, and the total of the entire diagram must equal 35. Therefore the two circles of the Venn Diagram including just chocolate, just vanilla and the intersection must equal 25, with the just chocolate plus intersection side equalling 15 and the just vanilla plus intersection side equalling 13.
We know:
(A U B) = A + B – (A ∩ B)
We have found that (A U B) = 25 and we are trying to find (A ∩ B). Plug in A and B
25 = 15 + 13 – (A ∩ B) = 28 – (A ∩ B)
or – (A ∩ B) = –3
(A ∩ B) = 3
← Didn't Know|Knew It →
In a population of cats, 10% are tabby colored, 5% are pregnant, and 3% are both tabby and pregnant. What is the probability that a cat is tabby but not pregnant?
In a population of cats, 10% are tabby colored, 5% are pregnant, and 3% are both tabby and pregnant. What is the probability that a cat is tabby but not pregnant?
Tap to reveal answer
Probability (tabby but not pregnant)
= Prob (tabby) – Prob (tabby and pregnant)
= 10% - 3%
= 7%
Probability (tabby but not pregnant)
= Prob (tabby) – Prob (tabby and pregnant)
= 10% - 3%
= 7%
← Didn't Know|Knew It →
At an overpriced department store there are  customers. If
customers. If  have purchased shirts,
have purchased shirts,  have purchased pants, and
have purchased pants, and  have purchased neither, how many purchased both shirts and pants?
have purchased neither, how many purchased both shirts and pants?
At an overpriced department store there are 



Tap to reveal answer
A way of solving this problem is by drawing a Venn diagram based on what is known:

There are  customers; within them there are those that purchased something (pants, shirts, or possibly a combination), and those that purchased nothing.
customers; within them there are those that purchased something (pants, shirts, or possibly a combination), and those that purchased nothing.
The amount of individuals that purchased something is given as:

The reason that the number of shoppers that bought both is subtracted is so that it is not counted twice when the customers that bought pants and the customers that bought shirts are added together.
Since  bought nothing,
bought nothing,

The amount that bought both then is:


A way of solving this problem is by drawing a Venn diagram based on what is known:

There are 
The amount of individuals that purchased something is given as:
The reason that the number of shoppers that bought both is subtracted is so that it is not counted twice when the customers that bought pants and the customers that bought shirts are added together.
Since 
The amount that bought both then is:
← Didn't Know|Knew It →
In a school, 70 students are taking classes. 35 of them will be taking Accounting and 20 of them will be taking Economics. 7 of them are taking both of these classes. How many of the students are not in either class?
In a school, 70 students are taking classes. 35 of them will be taking Accounting and 20 of them will be taking Economics. 7 of them are taking both of these classes. How many of the students are not in either class?
Tap to reveal answer
When you add both class rosters you get a total of 55 students
 .
.
You must subtract the 7 that are in both because they are counted twice in the 55
 .
.
The total in neither class will be the total students minus the adjusted enrollment in both classes
 .
.
When you add both class rosters you get a total of 55 students

You must subtract the 7 that are in both because they are counted twice in the 55

The total in neither class will be the total students minus the adjusted enrollment in both classes

← Didn't Know|Knew It →
A given company has 1500 employees. Of those employees, 800 are computer science majors. 25% of those computer science majors are also mathematics majors. That group of computer science/math dual majors makes up one third of the total mathematics majors. How many employees have majors other than computer science and mathematics?
A given company has 1500 employees. Of those employees, 800 are computer science majors. 25% of those computer science majors are also mathematics majors. That group of computer science/math dual majors makes up one third of the total mathematics majors. How many employees have majors other than computer science and mathematics?
Tap to reveal answer
Refer to the following Venn Diagram:
If 25% of the 800 CS students are also mathematics students, the number of students sharing these majors is 800 * 0.25 or 200 students. Furthermore, if this represents one third of the total of math students, we then know:
Math students * 1/3 = 200 or (1/3)M = 200
Solving for M we get 600. This means that the number of students that are ONLY math students is 400.
Looking at our diagram above, we must be careful not to "double add" the intersection. The easiest way to do this is to take the intersection and add to it the number of CS-only and math-only students: 600 + 200 + 400 = 1200. This number represents the total number of students that have either a math or CS major (that is, the number of students in the union of the two sets). This leaves 1500 – 1200 or 300 students.
Refer to the following Venn Diagram:
If 25% of the 800 CS students are also mathematics students, the number of students sharing these majors is 800 * 0.25 or 200 students. Furthermore, if this represents one third of the total of math students, we then know:
Math students * 1/3 = 200 or (1/3)M = 200
Solving for M we get 600. This means that the number of students that are ONLY math students is 400.
Looking at our diagram above, we must be careful not to "double add" the intersection. The easiest way to do this is to take the intersection and add to it the number of CS-only and math-only students: 600 + 200 + 400 = 1200. This number represents the total number of students that have either a math or CS major (that is, the number of students in the union of the two sets). This leaves 1500 – 1200 or 300 students.
← Didn't Know|Knew It →
In a class, there are 15 students who like chocolate. 13 students like vanilla. 10 students like neither. If there are 35 people in the class, how many students like chocolate and vanilla?
In a class, there are 15 students who like chocolate. 13 students like vanilla. 10 students like neither. If there are 35 people in the class, how many students like chocolate and vanilla?
Tap to reveal answer
In order to find the intersection of chocolate and vanilla, it is easiest to make a Venn Diagram. The outside of the Venn Diagram is 10, and the total of the entire diagram must equal 35. Therefore the two circles of the Venn Diagram including just chocolate, just vanilla and the intersection must equal 25, with the just chocolate plus intersection side equalling 15 and the just vanilla plus intersection side equalling 13.
We know:
(A U B) = A + B – (A ∩ B)
We have found that (A U B) = 25 and we are trying to find (A ∩ B). Plug in A and B
25 = 15 + 13 – (A ∩ B) = 28 – (A ∩ B)
or – (A ∩ B) = –3
(A ∩ B) = 3
In order to find the intersection of chocolate and vanilla, it is easiest to make a Venn Diagram. The outside of the Venn Diagram is 10, and the total of the entire diagram must equal 35. Therefore the two circles of the Venn Diagram including just chocolate, just vanilla and the intersection must equal 25, with the just chocolate plus intersection side equalling 15 and the just vanilla plus intersection side equalling 13.
We know:
(A U B) = A + B – (A ∩ B)
We have found that (A U B) = 25 and we are trying to find (A ∩ B). Plug in A and B
25 = 15 + 13 – (A ∩ B) = 28 – (A ∩ B)
or – (A ∩ B) = –3
(A ∩ B) = 3
← Didn't Know|Knew It →
