DSQ: Calculating the length of the side of a quadrilateral - GMAT Quantitative
Card 1 of 40
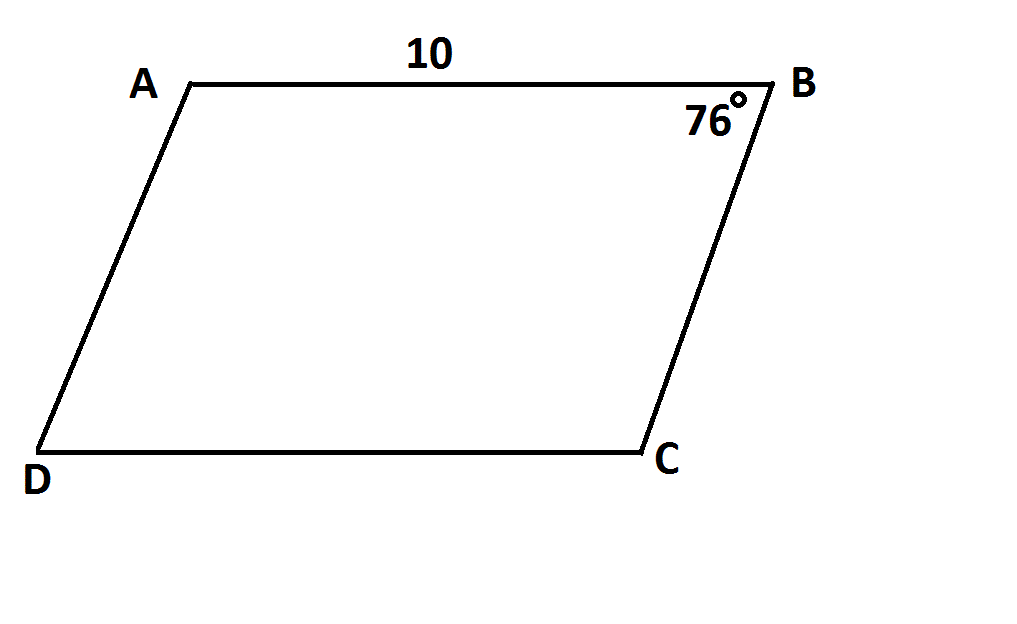
NOTE: Figure NOT drawn to scale.
Is the above figure a parallelogram?
Statement 1: 
Statement 2: 
NOTE: Figure NOT drawn to scale.
Is the above figure a parallelogram?
Statement 1:
Statement 2:
Tap to reveal answer
Knowing one pair of sides of a quadrilateral to be congruent is not alone sufficient to prove that figure to be a parallelogram, nor is knowing one pair of sides of a quadrilateral to be parallel. But knowing both about the same pair of sides is sufficient by a theorem of parallelograms.
Knowing one pair of sides of a quadrilateral to be congruent is not alone sufficient to prove that figure to be a parallelogram, nor is knowing one pair of sides of a quadrilateral to be parallel. But knowing both about the same pair of sides is sufficient by a theorem of parallelograms.
← Didn't Know|Knew It →
Notes: 
refers to the length of the entire dashed line. Figure not drawn to scale.
Calculate 
, the height of the large trapezoid.
Statement 1: 
Statement 2: The area of the trapezoid is 7,000.
Notes:
Calculate
Statement 1:
Statement 2: The area of the trapezoid is 7,000.
Tap to reveal answer
Consider the area formula for a trapezoid:
is the _midsegment_of the trapezoid, which, by the Trapezoid Midsegment Theorem, has length equal to the mean of the bases - in other words, 
. The area formula can be expressed, after substitution, as
So, if you know both the area and 
- but not just one - you can find the height by dividing.
Consider the area formula for a trapezoid:
So, if you know both the area and
← Didn't Know|Knew It →
Consider isosceles trapezoid 
.
I) 
has a perimeter of 
.
II) The larger base of 
is 45 times bigger than the smaller base.
Find the length of the two legs of 
.
Consider isosceles trapezoid
I)
II) The larger base of
Find the length of the two legs of
Tap to reveal answer
Consider isosceles trapezoid 
.
I) 
has a perimeter of 
.
II) The larger base of 
is 45 times bigger than the smaller base.
Find the length of the two legs of 
.
To find the length of the legs of a trapezoid, we need the perimeter and the two bases. Then, we can subtract the sum of the two bases from the perimeter and divide by two to find the lengths of the sides we are looking for.
Statement I gives us the perimeter of 
.
Statement II relates the two bases of 
.
We are told that 
is an isosceles trapezoid, which means its two legs are equal; however, we still have too many unknowns and not enough equations. There is no way to solve this without more information.
We still have three unknowns and two equations, so we cannot solve this system of equations.
Consider isosceles trapezoid
I)
II) The larger base of
Find the length of the two legs of
To find the length of the legs of a trapezoid, we need the perimeter and the two bases. Then, we can subtract the sum of the two bases from the perimeter and divide by two to find the lengths of the sides we are looking for.
Statement I gives us the perimeter of
Statement II relates the two bases of
We are told that
We still have three unknowns and two equations, so we cannot solve this system of equations.
← Didn't Know|Knew It →
Consider parallelogram 
.
I) The perimeter of 
is 
light years.
II) Side 
is 
light years and is equivalent to side 
.
Find the length of side 
.
Consider parallelogram
I) The perimeter of
II) Side
Find the length of side
Tap to reveal answer
We can work backwards from the perimeter to find the length of the unknown side.
I) Gives us the perimeter.
II) Gives us two of the sides.
In a parallelogram there are two sets of corresponding sides. We can use I) and II) to write the following equaiton, where l is the length of our wanted side.
Solve for l to find our final side:
We can work backwards from the perimeter to find the length of the unknown side.
I) Gives us the perimeter.
II) Gives us two of the sides.
In a parallelogram there are two sets of corresponding sides. We can use I) and II) to write the following equaiton, where l is the length of our wanted side.
Solve for l to find our final side:
← Didn't Know|Knew It →
Calculate the side of a square.
Statement 1: A circle with an area of 
is enclosed inside the square and touches all four edges of the square.
Statement 2: A circle with a circumference of 
encloses the square and touches all four corners of the square.
Calculate the side of a square.
Statement 1: A circle with an area of
Statement 2: A circle with a circumference of
Tap to reveal answer
Statement 1: A circle with an area of 
is enclosed inside the square and touches all four edges of the square.
Write the formula for the area of the circle.
After substituting the value of the area and solve for radius, the radius is 1. The side length of the square is double the length of the radius.
Statement 2: A circle with a circumference of 
encloses the square and touches all four corners of the square.
Write the formula for the circumference of the circle.
After substituting the value of the circumference and solve for diameter, the diameter of the circle is 1. This diameter represents the diagonal of the square. Because the square length and width are equal dimensions, it is possible to solve for the lengths of the square by Pythagorean Theorem knowing just the length of the square diagonal.
Therefore:
Statement 1: A circle with an area of
Write the formula for the area of the circle.
After substituting the value of the area and solve for radius, the radius is 1. The side length of the square is double the length of the radius.
Statement 2: A circle with a circumference of
Write the formula for the circumference of the circle.
After substituting the value of the circumference and solve for diameter, the diameter of the circle is 1. This diameter represents the diagonal of the square. Because the square length and width are equal dimensions, it is possible to solve for the lengths of the square by Pythagorean Theorem knowing just the length of the square diagonal.
Therefore:
← Didn't Know|Knew It →
NOTE: Figure NOT drawn to scale.
Is the above figure a parallelogram?
Statement 1:
Statement 2:
NOTE: Figure NOT drawn to scale.
Is the above figure a parallelogram?
Statement 1:
Statement 2:
Tap to reveal answer
Knowing one pair of sides of a quadrilateral to be congruent is not alone sufficient to prove that figure to be a parallelogram, nor is knowing one pair of sides of a quadrilateral to be parallel. But knowing both about the same pair of sides is sufficient by a theorem of parallelograms.
Knowing one pair of sides of a quadrilateral to be congruent is not alone sufficient to prove that figure to be a parallelogram, nor is knowing one pair of sides of a quadrilateral to be parallel. But knowing both about the same pair of sides is sufficient by a theorem of parallelograms.
← Didn't Know|Knew It →
Notes: refers to the length of the entire dashed line. Figure not drawn to scale.
Calculate , the height of the large trapezoid.
Statement 1:
Statement 2: The area of the trapezoid is 7,000.
Notes:
Calculate
Statement 1:
Statement 2: The area of the trapezoid is 7,000.
Tap to reveal answer
Consider the area formula for a trapezoid:
is the _midsegment_of the trapezoid, which, by the Trapezoid Midsegment Theorem, has length equal to the mean of the bases - in other words, . The area formula can be expressed, after substitution, as
So, if you know both the area and - but not just one - you can find the height by dividing.
Consider the area formula for a trapezoid:
So, if you know both the area and
← Didn't Know|Knew It →
Consider isosceles trapezoid .
I) has a perimeter of .
II) The larger base of is 45 times bigger than the smaller base.
Find the length of the two legs of .
Consider isosceles trapezoid
I)
II) The larger base of
Find the length of the two legs of
Tap to reveal answer
Consider isosceles trapezoid .
I) has a perimeter of .
II) The larger base of is 45 times bigger than the smaller base.
Find the length of the two legs of .
To find the length of the legs of a trapezoid, we need the perimeter and the two bases. Then, we can subtract the sum of the two bases from the perimeter and divide by two to find the lengths of the sides we are looking for.
Statement I gives us the perimeter of .
Statement II relates the two bases of .
We are told that is an isosceles trapezoid, which means its two legs are equal; however, we still have too many unknowns and not enough equations. There is no way to solve this without more information.
We still have three unknowns and two equations, so we cannot solve this system of equations.
Consider isosceles trapezoid
I)
II) The larger base of
Find the length of the two legs of
To find the length of the legs of a trapezoid, we need the perimeter and the two bases. Then, we can subtract the sum of the two bases from the perimeter and divide by two to find the lengths of the sides we are looking for.
Statement I gives us the perimeter of
Statement II relates the two bases of
We are told that
We still have three unknowns and two equations, so we cannot solve this system of equations.
← Didn't Know|Knew It →
Consider parallelogram .
I) The perimeter of is light years.
II) Side is light years and is equivalent to side .
Find the length of side .
Consider parallelogram
I) The perimeter of
II) Side
Find the length of side
Tap to reveal answer
We can work backwards from the perimeter to find the length of the unknown side.
I) Gives us the perimeter.
II) Gives us two of the sides.
In a parallelogram there are two sets of corresponding sides. We can use I) and II) to write the following equaiton, where l is the length of our wanted side.
Solve for l to find our final side:
We can work backwards from the perimeter to find the length of the unknown side.
I) Gives us the perimeter.
II) Gives us two of the sides.
In a parallelogram there are two sets of corresponding sides. We can use I) and II) to write the following equaiton, where l is the length of our wanted side.
Solve for l to find our final side:
← Didn't Know|Knew It →
Calculate the side of a square.
Statement 1: A circle with an area of is enclosed inside the square and touches all four edges of the square.
Statement 2: A circle with a circumference of encloses the square and touches all four corners of the square.
Calculate the side of a square.
Statement 1: A circle with an area of
Statement 2: A circle with a circumference of
Tap to reveal answer
Statement 1: A circle with an area of is enclosed inside the square and touches all four edges of the square.
Write the formula for the area of the circle.
After substituting the value of the area and solve for radius, the radius is 1. The side length of the square is double the length of the radius.
Statement 2: A circle with a circumference of encloses the square and touches all four corners of the square.
Write the formula for the circumference of the circle.
After substituting the value of the circumference and solve for diameter, the diameter of the circle is 1. This diameter represents the diagonal of the square. Because the square length and width are equal dimensions, it is possible to solve for the lengths of the square by Pythagorean Theorem knowing just the length of the square diagonal.
Therefore:
Statement 1: A circle with an area of
Write the formula for the area of the circle.
After substituting the value of the area and solve for radius, the radius is 1. The side length of the square is double the length of the radius.
Statement 2: A circle with a circumference of
Write the formula for the circumference of the circle.
After substituting the value of the circumference and solve for diameter, the diameter of the circle is 1. This diameter represents the diagonal of the square. Because the square length and width are equal dimensions, it is possible to solve for the lengths of the square by Pythagorean Theorem knowing just the length of the square diagonal.
Therefore:
← Didn't Know|Knew It →
NOTE: Figure NOT drawn to scale.
Is the above figure a parallelogram?
Statement 1:
Statement 2:
NOTE: Figure NOT drawn to scale.
Is the above figure a parallelogram?
Statement 1:
Statement 2:
Tap to reveal answer
Knowing one pair of sides of a quadrilateral to be congruent is not alone sufficient to prove that figure to be a parallelogram, nor is knowing one pair of sides of a quadrilateral to be parallel. But knowing both about the same pair of sides is sufficient by a theorem of parallelograms.
Knowing one pair of sides of a quadrilateral to be congruent is not alone sufficient to prove that figure to be a parallelogram, nor is knowing one pair of sides of a quadrilateral to be parallel. But knowing both about the same pair of sides is sufficient by a theorem of parallelograms.
← Didn't Know|Knew It →
Notes: refers to the length of the entire dashed line. Figure not drawn to scale.
Calculate , the height of the large trapezoid.
Statement 1:
Statement 2: The area of the trapezoid is 7,000.
Notes:
Calculate
Statement 1:
Statement 2: The area of the trapezoid is 7,000.
Tap to reveal answer
Consider the area formula for a trapezoid:
is the _midsegment_of the trapezoid, which, by the Trapezoid Midsegment Theorem, has length equal to the mean of the bases - in other words, . The area formula can be expressed, after substitution, as
So, if you know both the area and - but not just one - you can find the height by dividing.
Consider the area formula for a trapezoid:
So, if you know both the area and
← Didn't Know|Knew It →
Consider isosceles trapezoid .
I) has a perimeter of .
II) The larger base of is 45 times bigger than the smaller base.
Find the length of the two legs of .
Consider isosceles trapezoid
I)
II) The larger base of
Find the length of the two legs of
Tap to reveal answer
Consider isosceles trapezoid .
I) has a perimeter of .
II) The larger base of is 45 times bigger than the smaller base.
Find the length of the two legs of .
To find the length of the legs of a trapezoid, we need the perimeter and the two bases. Then, we can subtract the sum of the two bases from the perimeter and divide by two to find the lengths of the sides we are looking for.
Statement I gives us the perimeter of .
Statement II relates the two bases of .
We are told that is an isosceles trapezoid, which means its two legs are equal; however, we still have too many unknowns and not enough equations. There is no way to solve this without more information.
We still have three unknowns and two equations, so we cannot solve this system of equations.
Consider isosceles trapezoid
I)
II) The larger base of
Find the length of the two legs of
To find the length of the legs of a trapezoid, we need the perimeter and the two bases. Then, we can subtract the sum of the two bases from the perimeter and divide by two to find the lengths of the sides we are looking for.
Statement I gives us the perimeter of
Statement II relates the two bases of
We are told that
We still have three unknowns and two equations, so we cannot solve this system of equations.
← Didn't Know|Knew It →
Consider parallelogram .
I) The perimeter of is light years.
II) Side is light years and is equivalent to side .
Find the length of side .
Consider parallelogram
I) The perimeter of
II) Side
Find the length of side
Tap to reveal answer
We can work backwards from the perimeter to find the length of the unknown side.
I) Gives us the perimeter.
II) Gives us two of the sides.
In a parallelogram there are two sets of corresponding sides. We can use I) and II) to write the following equaiton, where l is the length of our wanted side.
Solve for l to find our final side:
We can work backwards from the perimeter to find the length of the unknown side.
I) Gives us the perimeter.
II) Gives us two of the sides.
In a parallelogram there are two sets of corresponding sides. We can use I) and II) to write the following equaiton, where l is the length of our wanted side.
Solve for l to find our final side:
← Didn't Know|Knew It →
Calculate the side of a square.
Statement 1: A circle with an area of is enclosed inside the square and touches all four edges of the square.
Statement 2: A circle with a circumference of encloses the square and touches all four corners of the square.
Calculate the side of a square.
Statement 1: A circle with an area of
Statement 2: A circle with a circumference of
Tap to reveal answer
Statement 1: A circle with an area of is enclosed inside the square and touches all four edges of the square.
Write the formula for the area of the circle.
After substituting the value of the area and solve for radius, the radius is 1. The side length of the square is double the length of the radius.
Statement 2: A circle with a circumference of encloses the square and touches all four corners of the square.
Write the formula for the circumference of the circle.
After substituting the value of the circumference and solve for diameter, the diameter of the circle is 1. This diameter represents the diagonal of the square. Because the square length and width are equal dimensions, it is possible to solve for the lengths of the square by Pythagorean Theorem knowing just the length of the square diagonal.
Therefore:
Statement 1: A circle with an area of
Write the formula for the area of the circle.
After substituting the value of the area and solve for radius, the radius is 1. The side length of the square is double the length of the radius.
Statement 2: A circle with a circumference of
Write the formula for the circumference of the circle.
After substituting the value of the circumference and solve for diameter, the diameter of the circle is 1. This diameter represents the diagonal of the square. Because the square length and width are equal dimensions, it is possible to solve for the lengths of the square by Pythagorean Theorem knowing just the length of the square diagonal.
Therefore:
← Didn't Know|Knew It →
NOTE: Figure NOT drawn to scale.
Is the above figure a parallelogram?
Statement 1:
Statement 2:
NOTE: Figure NOT drawn to scale.
Is the above figure a parallelogram?
Statement 1:
Statement 2:
Tap to reveal answer
Knowing one pair of sides of a quadrilateral to be congruent is not alone sufficient to prove that figure to be a parallelogram, nor is knowing one pair of sides of a quadrilateral to be parallel. But knowing both about the same pair of sides is sufficient by a theorem of parallelograms.
Knowing one pair of sides of a quadrilateral to be congruent is not alone sufficient to prove that figure to be a parallelogram, nor is knowing one pair of sides of a quadrilateral to be parallel. But knowing both about the same pair of sides is sufficient by a theorem of parallelograms.
← Didn't Know|Knew It →
Notes: refers to the length of the entire dashed line. Figure not drawn to scale.
Calculate , the height of the large trapezoid.
Statement 1:
Statement 2: The area of the trapezoid is 7,000.
Notes:
Calculate
Statement 1:
Statement 2: The area of the trapezoid is 7,000.
Tap to reveal answer
Consider the area formula for a trapezoid:
is the _midsegment_of the trapezoid, which, by the Trapezoid Midsegment Theorem, has length equal to the mean of the bases - in other words, . The area formula can be expressed, after substitution, as
So, if you know both the area and - but not just one - you can find the height by dividing.
Consider the area formula for a trapezoid:
So, if you know both the area and
← Didn't Know|Knew It →
Consider isosceles trapezoid .
I) has a perimeter of .
II) The larger base of is 45 times bigger than the smaller base.
Find the length of the two legs of .
Consider isosceles trapezoid
I)
II) The larger base of
Find the length of the two legs of
Tap to reveal answer
Consider isosceles trapezoid .
I) has a perimeter of .
II) The larger base of is 45 times bigger than the smaller base.
Find the length of the two legs of .
To find the length of the legs of a trapezoid, we need the perimeter and the two bases. Then, we can subtract the sum of the two bases from the perimeter and divide by two to find the lengths of the sides we are looking for.
Statement I gives us the perimeter of .
Statement II relates the two bases of .
We are told that is an isosceles trapezoid, which means its two legs are equal; however, we still have too many unknowns and not enough equations. There is no way to solve this without more information.
We still have three unknowns and two equations, so we cannot solve this system of equations.
Consider isosceles trapezoid
I)
II) The larger base of
Find the length of the two legs of
To find the length of the legs of a trapezoid, we need the perimeter and the two bases. Then, we can subtract the sum of the two bases from the perimeter and divide by two to find the lengths of the sides we are looking for.
Statement I gives us the perimeter of
Statement II relates the two bases of
We are told that
We still have three unknowns and two equations, so we cannot solve this system of equations.
← Didn't Know|Knew It →
Consider parallelogram .
I) The perimeter of is light years.
II) Side is light years and is equivalent to side .
Find the length of side .
Consider parallelogram
I) The perimeter of
II) Side
Find the length of side
Tap to reveal answer
We can work backwards from the perimeter to find the length of the unknown side.
I) Gives us the perimeter.
II) Gives us two of the sides.
In a parallelogram there are two sets of corresponding sides. We can use I) and II) to write the following equaiton, where l is the length of our wanted side.
Solve for l to find our final side:
We can work backwards from the perimeter to find the length of the unknown side.
I) Gives us the perimeter.
II) Gives us two of the sides.
In a parallelogram there are two sets of corresponding sides. We can use I) and II) to write the following equaiton, where l is the length of our wanted side.
Solve for l to find our final side:
← Didn't Know|Knew It →
Calculate the side of a square.
Statement 1: A circle with an area of is enclosed inside the square and touches all four edges of the square.
Statement 2: A circle with a circumference of encloses the square and touches all four corners of the square.
Calculate the side of a square.
Statement 1: A circle with an area of
Statement 2: A circle with a circumference of
Tap to reveal answer
Statement 1: A circle with an area of is enclosed inside the square and touches all four edges of the square.
Write the formula for the area of the circle.
After substituting the value of the area and solve for radius, the radius is 1. The side length of the square is double the length of the radius.
Statement 2: A circle with a circumference of encloses the square and touches all four corners of the square.
Write the formula for the circumference of the circle.
After substituting the value of the circumference and solve for diameter, the diameter of the circle is 1. This diameter represents the diagonal of the square. Because the square length and width are equal dimensions, it is possible to solve for the lengths of the square by Pythagorean Theorem knowing just the length of the square diagonal.
Therefore:
Statement 1: A circle with an area of
Write the formula for the area of the circle.
After substituting the value of the area and solve for radius, the radius is 1. The side length of the square is double the length of the radius.
Statement 2: A circle with a circumference of
Write the formula for the circumference of the circle.
After substituting the value of the circumference and solve for diameter, the diameter of the circle is 1. This diameter represents the diagonal of the square. Because the square length and width are equal dimensions, it is possible to solve for the lengths of the square by Pythagorean Theorem knowing just the length of the square diagonal.
Therefore:
← Didn't Know|Knew It →