Trapezoids - Geometry
Card 1 of 176
What is the length of the diagonals of trapezoid  ? Assume the figure is an isoceles trapezoid.
? Assume the figure is an isoceles trapezoid.

What is the length of the diagonals of trapezoid 

Tap to reveal answer
To find the length of the diagonal, we need to use the Pythagorean Theorem. Therefore, we need to sketch the following triangle within trapezoid  :
:

We know that the base of the triangle has length  . By subtracting the top of the trapezoid from the bottom of the trapezoid, we get:
. By subtracting the top of the trapezoid from the bottom of the trapezoid, we get:

Dividing by two, we have the length of each additional side on the bottom of the trapezoid:

Adding these two values together, we get  .
.
The formula for the length of diagonal  uses the Pythagoreon Theorem:
uses the Pythagoreon Theorem:
 , where
, where  is the point between
is the point between  and
and  representing the base of the triangle.
representing the base of the triangle.
Plugging in our values, we get:




To find the length of the diagonal, we need to use the Pythagorean Theorem. Therefore, we need to sketch the following triangle within trapezoid 

We know that the base of the triangle has length 
Dividing by two, we have the length of each additional side on the bottom of the trapezoid:
Adding these two values together, we get 
The formula for the length of diagonal 




Plugging in our values, we get:
← Didn't Know|Knew It →
Find the length of the diagonals of this isosceles trapezoid, with  .
.

Find the length of the diagonals of this isosceles trapezoid, with 
Tap to reveal answer
To find the length of the diagonals, split the top side into 3 sections as shown below:

The two congruent sections plus 8 adds to 14.  , so the two congruent sections add to 6. They must each be 3. This means that the top of the right triangle with the diagonal as a hypotenuse must be 11, since
, so the two congruent sections add to 6. They must each be 3. This means that the top of the right triangle with the diagonal as a hypotenuse must be 11, since  .
.

We can solve for the diagonal, now pictured, using Pythagorean Theorem:


 take the square root of both sides
take the square root of both sides

To find the length of the diagonals, split the top side into 3 sections as shown below:
The two congruent sections plus 8 adds to 14. 

We can solve for the diagonal, now pictured, using Pythagorean Theorem:

← Didn't Know|Knew It →
Find the length of both diagonals of this quadrilateral.

Find the length of both diagonals of this quadrilateral.
Tap to reveal answer
All of the lengths with one mark have length 5, and all of the side lengths with two marks have length 4. With this knowledge, we can add side lengths together to find that one diagonal is the hypotenuse to this right triangle:

Using Pythagorean Theorem gives:


 take the square root of each side
take the square root of each side

Similarly, the other diagonal can be found with this right triangle:

Once again using Pythagorean Theorem gives an answer of 
All of the lengths with one mark have length 5, and all of the side lengths with two marks have length 4. With this knowledge, we can add side lengths together to find that one diagonal is the hypotenuse to this right triangle:
Using Pythagorean Theorem gives:

Similarly, the other diagonal can be found with this right triangle:
Once again using Pythagorean Theorem gives an answer of
← Didn't Know|Knew It →
Find the length of diagonal  of the trapezoid.
of the trapezoid.

Find the length of diagonal 

Tap to reveal answer
-
The diagonal  can be found from
can be found from  by using the Pythagorean Theorem.
by using the Pythagorean Theorem.
-
The length of the base of  ,
,  has to be found because
has to be found because  is the length of the base of
is the length of the base of  .
.
-
 .
.
-
Using the Pythagorean Theorem on  to find
to find  ,
,





- Using the Pythagorean Theorem on
 to find
to find  ,
,






-
The diagonal
can be found from
by using the Pythagorean Theorem.
-
The length of the base of
,
has to be found because
is the length of the base of
.
-
.
-
Using the Pythagorean Theorem on
to find
,
- Using the Pythagorean Theorem on
to find
,
← Didn't Know|Knew It →
Find the length of the diagonal of the isosceles trapezoid given below.
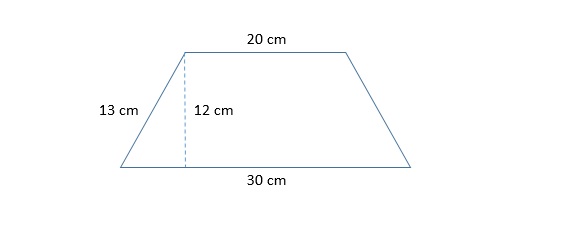
Find the length of the diagonal of the isosceles trapezoid given below.

Tap to reveal answer
In order to calculate the length of the diagonal, we first must assume that the height is perpendicular to both the top and bottom of the trapezoid.
Knowing this, we can draw in the diagonal as shown below and use the Pythagorean Theorem to solve for the diagonal.




We now take the square root of both sides:



In order to calculate the length of the diagonal, we first must assume that the height is perpendicular to both the top and bottom of the trapezoid.
Knowing this, we can draw in the diagonal as shown below and use the Pythagorean Theorem to solve for the diagonal.

We now take the square root of both sides:
← Didn't Know|Knew It →

Figure NOT drawn to scale.
Refer to the above diagram, which shows Trapezoid  with diagonal
with diagonal  . To the nearest whole number, give the length of
. To the nearest whole number, give the length of  .
.

Figure NOT drawn to scale.
Refer to the above diagram, which shows Trapezoid 


Tap to reveal answer
To illustrate how to determine the correct length, draw a perpendicular segment from  to
to  , calling the point of intersection
, calling the point of intersection  .
.

 divides the trapezoid into Rectangle
divides the trapezoid into Rectangle  and right triangle
and right triangle  .
.
Opposite sides of a rectangle are congruent, so  .
.
 . The two angles of a trapezoid along the same leg - in particular,
. The two angles of a trapezoid along the same leg - in particular,  and
and  - are supplementary, so
- are supplementary, so



By the 30-60-90 Triangle Theorem,

Opposite sides of a rectangle are congruent, so  , and
, and





 is the hypotenuse of right triangle
is the hypotenuse of right triangle  , so by the Pythagorean Theorem, its length can be calculated to be
, so by the Pythagorean Theorem, its length can be calculated to be

Set  and
and  :
:




To illustrate how to determine the correct length, draw a perpendicular segment from 






Opposite sides of a rectangle are congruent, so 



By the 30-60-90 Triangle Theorem,
Opposite sides of a rectangle are congruent, so 


Set 

← Didn't Know|Knew It →

Figure NOT drawn to scale.
Refer to the above diagram, which shows Trapezoid  with diagonal
with diagonal  . To the nearest whole number, give the length of
. To the nearest whole number, give the length of  .
.

Figure NOT drawn to scale.
Refer to the above diagram, which shows Trapezoid 


Tap to reveal answer
To illustrate how to determine the correct length, draw a perpendicular segment from  to
to  , calling the point of intersection
, calling the point of intersection  .
.

 divides the trapezoid into Rectangle
divides the trapezoid into Rectangle  and right triangle
and right triangle  .
.
Opposite sides of a rectangle are congruent, so  .
.
 . The two angles of a trapezoid along the same leg - in particular,
. The two angles of a trapezoid along the same leg - in particular,  and
and  - are supplementary, so
- are supplementary, so



By the 30-60-90 Triangle Theorem,

Opposite sides of a rectangle are congruent, so  , and
, and




 is the hypotenuse of right triangle
is the hypotenuse of right triangle  , so by the Pythagorean Theorem, its length can be calculated to be
, so by the Pythagorean Theorem, its length can be calculated to be

Set  and
and  :
:




To illustrate how to determine the correct length, draw a perpendicular segment from 






Opposite sides of a rectangle are congruent, so 



By the 30-60-90 Triangle Theorem,
Opposite sides of a rectangle are congruent, so 


Set 

← Didn't Know|Knew It →

Figure NOT drawn to scale.
Refer to the above diagram, which shows Trapezoid  with diagonal
with diagonal  . To the nearest whole number, give the length of
. To the nearest whole number, give the length of  .
.

Figure NOT drawn to scale.
Refer to the above diagram, which shows Trapezoid 


Tap to reveal answer
To illustrate how to determine the correct length, draw a perpendicular segment from  to
to  , calling the point of intersection
, calling the point of intersection  .
.

 divides the trapezoid into Rectangle
divides the trapezoid into Rectangle  and right triangle
and right triangle  .
.
Opposite sides of a rectangle are congruent, so  .
.
 . The two angles of a trapezoid along the same leg - in particular,
. The two angles of a trapezoid along the same leg - in particular,  and
and  - are supplementary, so
- are supplementary, so



By the 45-45-45 Triangle Theorem,

and

 is the hypotenuse of right triangle
is the hypotenuse of right triangle  , so by the Pythagorean Theorem, its length can be calculated to be
, so by the Pythagorean Theorem, its length can be calculated to be

Set  and
and  :
:




To illustrate how to determine the correct length, draw a perpendicular segment from 






Opposite sides of a rectangle are congruent, so 



By the 45-45-45 Triangle Theorem,
and


Set 

← Didn't Know|Knew It →
What is the length of the diagonals of trapezoid  ? Assume the figure is an isoceles trapezoid.
? Assume the figure is an isoceles trapezoid.

What is the length of the diagonals of trapezoid 

Tap to reveal answer
To find the length of the diagonal, we need to use the Pythagorean Theorem. Therefore, we need to sketch the following triangle within trapezoid  :
:

We know that the base of the triangle has length  . By subtracting the top of the trapezoid from the bottom of the trapezoid, we get:
. By subtracting the top of the trapezoid from the bottom of the trapezoid, we get:

Dividing by two, we have the length of each additional side on the bottom of the trapezoid:

Adding these two values together, we get  .
.
The formula for the length of diagonal  uses the Pythagoreon Theorem:
uses the Pythagoreon Theorem:
 , where
, where  is the point between
is the point between  and
and  representing the base of the triangle.
representing the base of the triangle.
Plugging in our values, we get:




To find the length of the diagonal, we need to use the Pythagorean Theorem. Therefore, we need to sketch the following triangle within trapezoid 

We know that the base of the triangle has length 
Dividing by two, we have the length of each additional side on the bottom of the trapezoid:
Adding these two values together, we get 
The formula for the length of diagonal 




Plugging in our values, we get:
← Didn't Know|Knew It →
Find the length of the diagonals of this isosceles trapezoid, with  .
.

Find the length of the diagonals of this isosceles trapezoid, with 
Tap to reveal answer
To find the length of the diagonals, split the top side into 3 sections as shown below:

The two congruent sections plus 8 adds to 14.  , so the two congruent sections add to 6. They must each be 3. This means that the top of the right triangle with the diagonal as a hypotenuse must be 11, since
, so the two congruent sections add to 6. They must each be 3. This means that the top of the right triangle with the diagonal as a hypotenuse must be 11, since  .
.

We can solve for the diagonal, now pictured, using Pythagorean Theorem:


 take the square root of both sides
take the square root of both sides

To find the length of the diagonals, split the top side into 3 sections as shown below:
The two congruent sections plus 8 adds to 14. 

We can solve for the diagonal, now pictured, using Pythagorean Theorem:

← Didn't Know|Knew It →
Find the length of both diagonals of this quadrilateral.

Find the length of both diagonals of this quadrilateral.
Tap to reveal answer
All of the lengths with one mark have length 5, and all of the side lengths with two marks have length 4. With this knowledge, we can add side lengths together to find that one diagonal is the hypotenuse to this right triangle:

Using Pythagorean Theorem gives:


 take the square root of each side
take the square root of each side

Similarly, the other diagonal can be found with this right triangle:

Once again using Pythagorean Theorem gives an answer of 
All of the lengths with one mark have length 5, and all of the side lengths with two marks have length 4. With this knowledge, we can add side lengths together to find that one diagonal is the hypotenuse to this right triangle:
Using Pythagorean Theorem gives:

Similarly, the other diagonal can be found with this right triangle:
Once again using Pythagorean Theorem gives an answer of
← Didn't Know|Knew It →
Find the length of diagonal  of the trapezoid.
of the trapezoid.

Find the length of diagonal 

Tap to reveal answer
-
The diagonal  can be found from
can be found from  by using the Pythagorean Theorem.
by using the Pythagorean Theorem.
-
The length of the base of  ,
,  has to be found because
has to be found because  is the length of the base of
is the length of the base of  .
.
-
 .
.
-
Using the Pythagorean Theorem on  to find
to find  ,
,





- Using the Pythagorean Theorem on
 to find
to find  ,
,






-
The diagonal
can be found from
by using the Pythagorean Theorem.
-
The length of the base of
,
has to be found because
is the length of the base of
.
-
.
-
Using the Pythagorean Theorem on
to find
,
- Using the Pythagorean Theorem on
to find
,
← Didn't Know|Knew It →
Find the length of the diagonal of the isosceles trapezoid given below.

Find the length of the diagonal of the isosceles trapezoid given below.

Tap to reveal answer
In order to calculate the length of the diagonal, we first must assume that the height is perpendicular to both the top and bottom of the trapezoid.
Knowing this, we can draw in the diagonal as shown below and use the Pythagorean Theorem to solve for the diagonal.




We now take the square root of both sides:



In order to calculate the length of the diagonal, we first must assume that the height is perpendicular to both the top and bottom of the trapezoid.
Knowing this, we can draw in the diagonal as shown below and use the Pythagorean Theorem to solve for the diagonal.

We now take the square root of both sides:
← Didn't Know|Knew It →

Figure NOT drawn to scale.
Refer to the above diagram, which shows Trapezoid  with diagonal
with diagonal  . To the nearest whole number, give the length of
. To the nearest whole number, give the length of  .
.

Figure NOT drawn to scale.
Refer to the above diagram, which shows Trapezoid 


Tap to reveal answer
To illustrate how to determine the correct length, draw a perpendicular segment from  to
to  , calling the point of intersection
, calling the point of intersection  .
.

 divides the trapezoid into Rectangle
divides the trapezoid into Rectangle  and right triangle
and right triangle  .
.
Opposite sides of a rectangle are congruent, so  .
.
 . The two angles of a trapezoid along the same leg - in particular,
. The two angles of a trapezoid along the same leg - in particular,  and
and  - are supplementary, so
- are supplementary, so



By the 30-60-90 Triangle Theorem,

Opposite sides of a rectangle are congruent, so  , and
, and





 is the hypotenuse of right triangle
is the hypotenuse of right triangle  , so by the Pythagorean Theorem, its length can be calculated to be
, so by the Pythagorean Theorem, its length can be calculated to be

Set  and
and  :
:




To illustrate how to determine the correct length, draw a perpendicular segment from 






Opposite sides of a rectangle are congruent, so 



By the 30-60-90 Triangle Theorem,
Opposite sides of a rectangle are congruent, so 


Set 

← Didn't Know|Knew It →

Figure NOT drawn to scale.
Refer to the above diagram, which shows Trapezoid  with diagonal
with diagonal  . To the nearest whole number, give the length of
. To the nearest whole number, give the length of  .
.

Figure NOT drawn to scale.
Refer to the above diagram, which shows Trapezoid 


Tap to reveal answer
To illustrate how to determine the correct length, draw a perpendicular segment from  to
to  , calling the point of intersection
, calling the point of intersection  .
.

 divides the trapezoid into Rectangle
divides the trapezoid into Rectangle  and right triangle
and right triangle  .
.
Opposite sides of a rectangle are congruent, so  .
.
 . The two angles of a trapezoid along the same leg - in particular,
. The two angles of a trapezoid along the same leg - in particular,  and
and  - are supplementary, so
- are supplementary, so



By the 30-60-90 Triangle Theorem,

Opposite sides of a rectangle are congruent, so  , and
, and




 is the hypotenuse of right triangle
is the hypotenuse of right triangle  , so by the Pythagorean Theorem, its length can be calculated to be
, so by the Pythagorean Theorem, its length can be calculated to be

Set  and
and  :
:




To illustrate how to determine the correct length, draw a perpendicular segment from 






Opposite sides of a rectangle are congruent, so 



By the 30-60-90 Triangle Theorem,
Opposite sides of a rectangle are congruent, so 


Set 

← Didn't Know|Knew It →

Figure NOT drawn to scale.
Refer to the above diagram, which shows Trapezoid  with diagonal
with diagonal  . To the nearest whole number, give the length of
. To the nearest whole number, give the length of  .
.

Figure NOT drawn to scale.
Refer to the above diagram, which shows Trapezoid 


Tap to reveal answer
To illustrate how to determine the correct length, draw a perpendicular segment from  to
to  , calling the point of intersection
, calling the point of intersection  .
.

 divides the trapezoid into Rectangle
divides the trapezoid into Rectangle  and right triangle
and right triangle  .
.
Opposite sides of a rectangle are congruent, so  .
.
 . The two angles of a trapezoid along the same leg - in particular,
. The two angles of a trapezoid along the same leg - in particular,  and
and  - are supplementary, so
- are supplementary, so



By the 45-45-45 Triangle Theorem,

and

 is the hypotenuse of right triangle
is the hypotenuse of right triangle  , so by the Pythagorean Theorem, its length can be calculated to be
, so by the Pythagorean Theorem, its length can be calculated to be

Set  and
and  :
:




To illustrate how to determine the correct length, draw a perpendicular segment from 






Opposite sides of a rectangle are congruent, so 



By the 45-45-45 Triangle Theorem,
and


Set 

← Didn't Know|Knew It →
Find the area of a trapezoid with bases of  and
and  and a height of
and a height of  .
.
Find the area of a trapezoid with bases of 


Tap to reveal answer
The formula for the area of a trapezoid is:

Where  and
and  are the bases and
are the bases and  is the height. Using this formula and the given values, we get:
is the height. Using this formula and the given values, we get:

The formula for the area of a trapezoid is:
Where 


← Didn't Know|Knew It →
What is the area of this regular trapezoid?

What is the area of this regular trapezoid?

Tap to reveal answer
To solve this question, you must divide the trapezoid into a rectangle and two right triangles. Using the Pythagorean Theorem, you would calculate the height of the triangle which is 4. The dimensions of the rectangle are 5 and 4, hence the area will be 20. The base of the triangle is 3 and the height of the triangle is 4. The area of one triangle is 6. Hence the total area will be 20+6+6=32. If you forget to split the shape into a rectangle and TWO triangles, or if you add the dimensions of the trapezoid, you could arrive at 26 as your answer.
To solve this question, you must divide the trapezoid into a rectangle and two right triangles. Using the Pythagorean Theorem, you would calculate the height of the triangle which is 4. The dimensions of the rectangle are 5 and 4, hence the area will be 20. The base of the triangle is 3 and the height of the triangle is 4. The area of one triangle is 6. Hence the total area will be 20+6+6=32. If you forget to split the shape into a rectangle and TWO triangles, or if you add the dimensions of the trapezoid, you could arrive at 26 as your answer.
← Didn't Know|Knew It →

What is the area of the trapezoid above if a = 2, b = 6, and h = 4?

What is the area of the trapezoid above if a = 2, b = 6, and h = 4?
Tap to reveal answer
Area of a Trapezoid = ½(a+b)*h
= ½ (2+6) * 4
= ½ (8) * 4
= 4 * 4 = 16
Area of a Trapezoid = ½(a+b)*h
= ½ (2+6) * 4
= ½ (8) * 4
= 4 * 4 = 16
← Didn't Know|Knew It →
A trapezoid has a base of length 4, another base of length s, and a height of length s. A square has sides of length s. What is the value of s such that the area of the trapezoid and the area of the square are equal?
A trapezoid has a base of length 4, another base of length s, and a height of length s. A square has sides of length s. What is the value of s such that the area of the trapezoid and the area of the square are equal?
Tap to reveal answer
In general, the formula for the area of a trapezoid is (1/2)(a + b)(h), where a and b are the lengths of the bases, and h is the length of the height. Thus, we can write the area for the trapezoid given in the problem as follows:
area of trapezoid = (1/2)(4 + s)(s)
Similarly, the area of a square with sides of length a is given by _a_2. Thus, the area of the square given in the problem is _s_2.
We now can set the area of the trapezoid equal to the area of the square and solve for s.
(1/2)(4 + s)(s) = _s_2
Multiply both sides by 2 to eliminate the 1/2.
(4 + s)(s) = 2_s_2
Distribute the s on the left.
4_s_ + _s_2 = 2_s_2
Subtract _s_2 from both sides.
4_s_ = _s_2
Because s must be a positive number, we can divide both sides by s.
4 = s
This means the value of s must be 4.
The answer is 4.
In general, the formula for the area of a trapezoid is (1/2)(a + b)(h), where a and b are the lengths of the bases, and h is the length of the height. Thus, we can write the area for the trapezoid given in the problem as follows:
area of trapezoid = (1/2)(4 + s)(s)
Similarly, the area of a square with sides of length a is given by _a_2. Thus, the area of the square given in the problem is _s_2.
We now can set the area of the trapezoid equal to the area of the square and solve for s.
(1/2)(4 + s)(s) = _s_2
Multiply both sides by 2 to eliminate the 1/2.
(4 + s)(s) = 2_s_2
Distribute the s on the left.
4_s_ + _s_2 = 2_s_2
Subtract _s_2 from both sides.
4_s_ = _s_2
Because s must be a positive number, we can divide both sides by s.
4 = s
This means the value of s must be 4.
The answer is 4.
← Didn't Know|Knew It →