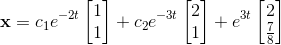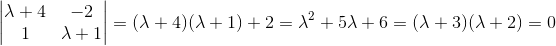First, we will need the complementary solution, and a fundamental matrix for the homogeneous system. Thus, we find the characteristic equation of the matrix given.

Using , we then find the eigenvectors by solving for the eigenspace.

This has solutions , or . So a suitable eigenvector is simply .

Repeating for ,

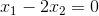
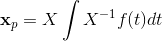
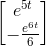
This has solutions , and thus a suitable eigenvector is . Thus, our complementary solution is and our fundamental matrix (though in this case, not the matrix exponential) is . Variation of parameters tells us that the particular solution is given by , so first we find using the inverse rule for 2x2 matrices. Thus, . Plugging in, we have . So .

Finishing up, we have .

Adding the particular solution to the homogeneous, we get a final general solution of