Higher-Order Differential Equations - Differential Equations
Card 1 of 80
Solve the initial value problem  for
for  and
and  .
.
Solve the initial value problem 


Tap to reveal answer
This is a linear higher order differential equation. First, we need the characteristic equation, which is just obtained by turning the derivative orders into powers to get the following:
 We then solve the characteristic equation and find that
We then solve the characteristic equation and find that This lets us know that the basis for the fundamental set of solutions to this problem (solutions to the homogeneous problem) contains
This lets us know that the basis for the fundamental set of solutions to this problem (solutions to the homogeneous problem) contains  .
.
As the given problem was homogeneous, the solution is just a linear combination of these functions. Thus,  . Plugging in our initial condition, we find that
. Plugging in our initial condition, we find that  . To plug in the second initial condition, we take the derivative and find that
. To plug in the second initial condition, we take the derivative and find that  . Plugging in the second initial condition yields
. Plugging in the second initial condition yields  . Solving this simple system of linear equations shows us that
. Solving this simple system of linear equations shows us that

Leaving us with a final answer of 
(Note, it would have been very simple to find the right answer just by taking derivatives and plugging in, but this is not overly helpful for non-multiple choice questions)
This is a linear higher order differential equation. First, we need the characteristic equation, which is just obtained by turning the derivative orders into powers to get the following:



As the given problem was homogeneous, the solution is just a linear combination of these functions. Thus, 



Leaving us with a final answer of
(Note, it would have been very simple to find the right answer just by taking derivatives and plugging in, but this is not overly helpful for non-multiple choice questions)
← Didn't Know|Knew It →
Solve the following homogeneous differential equation:

Solve the following homogeneous differential equation:
Tap to reveal answer
This differential equation has characteristic equation of:
 It must be noted that this characteristic equation has a double rootof r=5.
It must be noted that this characteristic equation has a double rootof r=5.
Thus the general solution to a homogeneous differential equation with a repeated root is used.
This is equation is
 in the case of a repeated root such as this,
in the case of a repeated root such as this,  and is the repeated root r=5.
and is the repeated root r=5.
Therefore, the solution is

This differential equation has characteristic equation of:

Thus the general solution to a homogeneous differential equation with a repeated root is used.
This is equation is


Therefore, the solution is
← Didn't Know|Knew It →
Solve the initial value problem  for
for  and
and 
Solve the initial value problem 

Tap to reveal answer
This is a linear higher order differential equation. First, we need the characteristic equation, which is just obtained by turning the derivative orders into powers to get the following:
 We then solve the characteristic equation and find that
We then solve the characteristic equation and find that (Use the quadratic formula if you'd like) This lets us know that the basis for the fundamental set of solutions to this problem (solutions to the homogeneous problem) contains
(Use the quadratic formula if you'd like) This lets us know that the basis for the fundamental set of solutions to this problem (solutions to the homogeneous problem) contains  .
.
As the given problem was homogeneous, the solution is just a linear combination of these functions. Thus,  . Plugging in our initial condition, we find that
. Plugging in our initial condition, we find that  . To plug in the second initial condition, we take the derivative and find that
. To plug in the second initial condition, we take the derivative and find that  . Plugging in the second initial condition yields
. Plugging in the second initial condition yields  . Solving this simple system of linear equations shows us that
. Solving this simple system of linear equations shows us that

Leaving us with a final answer of 
(Note, it would have been very simple to find the right answer just by taking derivatives and plugging in, but this is not overly helpful for non-multiple choice questions)
This is a linear higher order differential equation. First, we need the characteristic equation, which is just obtained by turning the derivative orders into powers to get the following:



As the given problem was homogeneous, the solution is just a linear combination of these functions. Thus, 



Leaving us with a final answer of
(Note, it would have been very simple to find the right answer just by taking derivatives and plugging in, but this is not overly helpful for non-multiple choice questions)
← Didn't Know|Knew It →
Find the general solution to  .
.
Find the general solution to 
Tap to reveal answer
This is a linear higher order differential equation. First, we need the characteristic equation, which is just obtained by turning the derivative orders into powers to get the following:
 To factor this, in this case we may use factoring by grouping. More generally, we may use horner's scheme/synthetic division to test possible roots. Here are both methods shown.
To factor this, in this case we may use factoring by grouping. More generally, we may use horner's scheme/synthetic division to test possible roots. Here are both methods shown.

Alternatively, the rational root theorem suggests that we try -1 or 1 as a root of this equation. Using horner's scheme, we see


Which tells us the the polynomial factors into  and that
and that  . This means that the fundamental set of solutions is
. This means that the fundamental set of solutions is 
As the given problem was homogeneous, the solution is just a linear combination of these functions. Thus,  . As this is not an initial value problem and just asks for the general solution, we are done.
. As this is not an initial value problem and just asks for the general solution, we are done.
This is a linear higher order differential equation. First, we need the characteristic equation, which is just obtained by turning the derivative orders into powers to get the following:

Alternatively, the rational root theorem suggests that we try -1 or 1 as a root of this equation. Using horner's scheme, we see
Which tells us the the polynomial factors into 

As the given problem was homogeneous, the solution is just a linear combination of these functions. Thus, 
← Didn't Know|Knew It →
Solve the following homogeneous differential equation:

Solve the following homogeneous differential equation:
Tap to reveal answer
The ode has a characteristic equation of  .
.
This yields the double root of r=2. Then the roots are plugged into the general solution to a homogeneous differential equation with a repeated root.
 (for real repeated roots)
(for real repeated roots)
Thus, the solution is,

The ode has a characteristic equation of 
This yields the double root of r=2. Then the roots are plugged into the general solution to a homogeneous differential equation with a repeated root.

Thus, the solution is,
← Didn't Know|Knew It →
Solve the General form of the differential equation:

Solve the General form of the differential equation:
Tap to reveal answer
This differential equation has a characteristic equation of
 , which yields the roots for r=2 and r=3. Once the roots or established to be real and non-repeated, the general solution for homogeneous linear ODEs is used. this equation is given as:
, which yields the roots for r=2 and r=3. Once the roots or established to be real and non-repeated, the general solution for homogeneous linear ODEs is used. this equation is given as:

with r being the roots of the characteristic equation.
Thus, the solution is

This differential equation has a characteristic equation of

with r being the roots of the characteristic equation.
Thus, the solution is
← Didn't Know|Knew It →
Solve the general homogeneous part of the following differential equation:

Solve the general homogeneous part of the following differential equation:
Tap to reveal answer
We start off by noting that the homogeneous equation we are trying to solve is given as
 .
.
This differential equation thus has characteristic equation of
 .
.
This has roots of r=3 and r=-4, therefore, the general homogeneous solution is given by:

We start off by noting that the homogeneous equation we are trying to solve is given as

This differential equation thus has characteristic equation of

This has roots of r=3 and r=-4, therefore, the general homogeneous solution is given by:
← Didn't Know|Knew It →
Find a general solution to the following Differential Equation

Find a general solution to the following Differential Equation
Tap to reveal answer
Solving the auxiliary equation

Trying out candidates for roots from the Rational Root Theorem we have a root  .
.
Factoring completely we have

Our general solution is

where  are arbitrary constants.
are arbitrary constants.
Solving the auxiliary equation
Trying out candidates for roots from the Rational Root Theorem we have a root 
Factoring completely we have
Our general solution is
where 
← Didn't Know|Knew It →
For the initial value problem


Which if the following intervals containing  do NOT guarantees the existence of a unique solution?
do NOT guarantees the existence of a unique solution?
For the initial value problem
Which if the following intervals containing 
Tap to reveal answer
Putting the equation in standard form we get that

We need to find where these coefficients are simultaneously continuous. This is where
 . The choice that is not a subset of these is
. The choice that is not a subset of these is 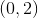
Putting the equation in standard form we get that
We need to find where these coefficients are simultaneously continuous. This is where

← Didn't Know|Knew It →
For the initial value problem


Which if the following intervals containing  do NOT guarantees the existence of a unique solution?
do NOT guarantees the existence of a unique solution?
For the initial value problem
Which if the following intervals containing 
Tap to reveal answer
Putting the equation in standard form we get that

We need to find where these coefficients are simultaneously continuous. This is where
 . The choice that is not a subset of these is
. The choice that is not a subset of these is 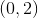
Putting the equation in standard form we get that
We need to find where these coefficients are simultaneously continuous. This is where

← Didn't Know|Knew It →
Solve the initial value problem  for
for  and
and  .
.
Solve the initial value problem 


Tap to reveal answer
This is a linear higher order differential equation. First, we need the characteristic equation, which is just obtained by turning the derivative orders into powers to get the following:
 We then solve the characteristic equation and find that
We then solve the characteristic equation and find that This lets us know that the basis for the fundamental set of solutions to this problem (solutions to the homogeneous problem) contains
This lets us know that the basis for the fundamental set of solutions to this problem (solutions to the homogeneous problem) contains  .
.
As the given problem was homogeneous, the solution is just a linear combination of these functions. Thus,  . Plugging in our initial condition, we find that
. Plugging in our initial condition, we find that  . To plug in the second initial condition, we take the derivative and find that
. To plug in the second initial condition, we take the derivative and find that  . Plugging in the second initial condition yields
. Plugging in the second initial condition yields  . Solving this simple system of linear equations shows us that
. Solving this simple system of linear equations shows us that

Leaving us with a final answer of 
(Note, it would have been very simple to find the right answer just by taking derivatives and plugging in, but this is not overly helpful for non-multiple choice questions)
This is a linear higher order differential equation. First, we need the characteristic equation, which is just obtained by turning the derivative orders into powers to get the following:



As the given problem was homogeneous, the solution is just a linear combination of these functions. Thus, 



Leaving us with a final answer of
(Note, it would have been very simple to find the right answer just by taking derivatives and plugging in, but this is not overly helpful for non-multiple choice questions)
← Didn't Know|Knew It →
Solve the following homogeneous differential equation:

Solve the following homogeneous differential equation:
Tap to reveal answer
This differential equation has characteristic equation of:
 It must be noted that this characteristic equation has a double rootof r=5.
It must be noted that this characteristic equation has a double rootof r=5.
Thus the general solution to a homogeneous differential equation with a repeated root is used.
This is equation is
 in the case of a repeated root such as this,
in the case of a repeated root such as this,  and is the repeated root r=5.
and is the repeated root r=5.
Therefore, the solution is

This differential equation has characteristic equation of:

Thus the general solution to a homogeneous differential equation with a repeated root is used.
This is equation is


Therefore, the solution is
← Didn't Know|Knew It →
Solve the initial value problem  for
for  and
and 
Solve the initial value problem 

Tap to reveal answer
This is a linear higher order differential equation. First, we need the characteristic equation, which is just obtained by turning the derivative orders into powers to get the following:
 We then solve the characteristic equation and find that
We then solve the characteristic equation and find that (Use the quadratic formula if you'd like) This lets us know that the basis for the fundamental set of solutions to this problem (solutions to the homogeneous problem) contains
(Use the quadratic formula if you'd like) This lets us know that the basis for the fundamental set of solutions to this problem (solutions to the homogeneous problem) contains  .
.
As the given problem was homogeneous, the solution is just a linear combination of these functions. Thus,  . Plugging in our initial condition, we find that
. Plugging in our initial condition, we find that  . To plug in the second initial condition, we take the derivative and find that
. To plug in the second initial condition, we take the derivative and find that  . Plugging in the second initial condition yields
. Plugging in the second initial condition yields  . Solving this simple system of linear equations shows us that
. Solving this simple system of linear equations shows us that

Leaving us with a final answer of 
(Note, it would have been very simple to find the right answer just by taking derivatives and plugging in, but this is not overly helpful for non-multiple choice questions)
This is a linear higher order differential equation. First, we need the characteristic equation, which is just obtained by turning the derivative orders into powers to get the following:



As the given problem was homogeneous, the solution is just a linear combination of these functions. Thus, 



Leaving us with a final answer of
(Note, it would have been very simple to find the right answer just by taking derivatives and plugging in, but this is not overly helpful for non-multiple choice questions)
← Didn't Know|Knew It →
Find the general solution to  .
.
Find the general solution to 
Tap to reveal answer
This is a linear higher order differential equation. First, we need the characteristic equation, which is just obtained by turning the derivative orders into powers to get the following:
 To factor this, in this case we may use factoring by grouping. More generally, we may use horner's scheme/synthetic division to test possible roots. Here are both methods shown.
To factor this, in this case we may use factoring by grouping. More generally, we may use horner's scheme/synthetic division to test possible roots. Here are both methods shown.

Alternatively, the rational root theorem suggests that we try -1 or 1 as a root of this equation. Using horner's scheme, we see


Which tells us the the polynomial factors into  and that
and that  . This means that the fundamental set of solutions is
. This means that the fundamental set of solutions is 
As the given problem was homogeneous, the solution is just a linear combination of these functions. Thus,  . As this is not an initial value problem and just asks for the general solution, we are done.
. As this is not an initial value problem and just asks for the general solution, we are done.
This is a linear higher order differential equation. First, we need the characteristic equation, which is just obtained by turning the derivative orders into powers to get the following:

Alternatively, the rational root theorem suggests that we try -1 or 1 as a root of this equation. Using horner's scheme, we see
Which tells us the the polynomial factors into 

As the given problem was homogeneous, the solution is just a linear combination of these functions. Thus, 
← Didn't Know|Knew It →
Solve the following homogeneous differential equation:

Solve the following homogeneous differential equation:
Tap to reveal answer
The ode has a characteristic equation of  .
.
This yields the double root of r=2. Then the roots are plugged into the general solution to a homogeneous differential equation with a repeated root.
 (for real repeated roots)
(for real repeated roots)
Thus, the solution is,

The ode has a characteristic equation of 
This yields the double root of r=2. Then the roots are plugged into the general solution to a homogeneous differential equation with a repeated root.

Thus, the solution is,
← Didn't Know|Knew It →
Solve the General form of the differential equation:

Solve the General form of the differential equation:
Tap to reveal answer
This differential equation has a characteristic equation of
 , which yields the roots for r=2 and r=3. Once the roots or established to be real and non-repeated, the general solution for homogeneous linear ODEs is used. this equation is given as:
, which yields the roots for r=2 and r=3. Once the roots or established to be real and non-repeated, the general solution for homogeneous linear ODEs is used. this equation is given as:

with r being the roots of the characteristic equation.
Thus, the solution is

This differential equation has a characteristic equation of

with r being the roots of the characteristic equation.
Thus, the solution is
← Didn't Know|Knew It →
Solve the general homogeneous part of the following differential equation:

Solve the general homogeneous part of the following differential equation:
Tap to reveal answer
We start off by noting that the homogeneous equation we are trying to solve is given as
 .
.
This differential equation thus has characteristic equation of
 .
.
This has roots of r=3 and r=-4, therefore, the general homogeneous solution is given by:

We start off by noting that the homogeneous equation we are trying to solve is given as

This differential equation thus has characteristic equation of

This has roots of r=3 and r=-4, therefore, the general homogeneous solution is given by:
← Didn't Know|Knew It →
Find a general solution to the following Differential Equation

Find a general solution to the following Differential Equation
Tap to reveal answer
Solving the auxiliary equation

Trying out candidates for roots from the Rational Root Theorem we have a root  .
.
Factoring completely we have

Our general solution is

where  are arbitrary constants.
are arbitrary constants.
Solving the auxiliary equation
Trying out candidates for roots from the Rational Root Theorem we have a root 
Factoring completely we have
Our general solution is
where 
← Didn't Know|Knew It →
Solve the given differential equation by undetermined coefficients.

Solve the given differential equation by undetermined coefficients.
Tap to reveal answer
First solve the homogeneous portion:

Therefore,  is a repeated root thus one of the complimentary solutions
is a repeated root thus one of the complimentary solutions  is,
is,

Now find the remaining complimentary solution  .
.

Now solve for  and
and  .
.

Where

and

Therefore,

Now, combine both of the complimentary solutions together to arrive at the general solution.

First solve the homogeneous portion:
Therefore, 

Now find the remaining complimentary solution 
Now solve for 

Where
and
Therefore,
Now, combine both of the complimentary solutions together to arrive at the general solution.
← Didn't Know|Knew It →
Find the general solution for  .
.
Find the general solution for 
Tap to reveal answer
This is a higher order inhomogeneous linear differential equation. Because the inhomogeneity is a cosine, we will use variation of parameters to solve it.
First, we find the characteristic equation to solve for the homogenous solution. This gives us  .
.
This tells us that the homogeneous solution is  . As neither of these overlap with our inhomogeneity, we are safe to continue without adding a factor of t.
. As neither of these overlap with our inhomogeneity, we are safe to continue without adding a factor of t.
Thus, let us guess that  . Then,
. Then,
 and
and

Plugging into the original equation, we have

Which implies that  and
and  . Solving via substitution,
. Solving via substitution,



Thus, the particular solution is  and the overall solution is the particular plus the homogeneous.
and the overall solution is the particular plus the homogeneous.
So

This is a higher order inhomogeneous linear differential equation. Because the inhomogeneity is a cosine, we will use variation of parameters to solve it.
First, we find the characteristic equation to solve for the homogenous solution. This gives us 
This tells us that the homogeneous solution is 
Thus, let us guess that 

Plugging into the original equation, we have
Which implies that 

Thus, the particular solution is 
So
← Didn't Know|Knew It →