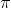Complex Functions

Help Questions

Complex Analysis › Complex Functions

Questions 1 - 2

1

Consider the function

Find an expression for (hint: use the definition of derivatve) and where it exists in the complex plane.

$f'(z) = 0 \text{ where } z=0$

$f'(z) = 2|z| \text{ where } z=0$

$f'(z) = 2|z| \text{ } \forall z$

$f'(z) = 2z \text{ } \forall z$

$f'(z) = 2z \text{ where } z=0$

Explanation

Applying the definition of derivative, we have that

$f'(z) = \lim_{\Delta z \to 0} \frac{f(z+\Delta z) - f(z)}{\Delta z} \$

$f'(z) = \lim_{\Delta z \to 0}\frac{|z+\Delta z|^2 - |z|^2}{\Delta z} = \lim_{\Delta z \to 0} \frac{(z+\Delta z)(\bar{z}+\overline{\Delta z}) - z\overline{z}}{\Delta z} = \lim_{\Delta z \to 0} \overline{z} + \overline{\Delta z} + z \frac{\overline{\Delta z}}{\Delta z}$

If the limits exists, it can be found by letting $\Delta z$ approach in any manner.

In particular, if we it approach through the points $(\Delta x , 0 )$ , we have that

$\overline{\Delta z} = \overline{\Delta x + i0} = \Delta x - i0 = \Delta x + i0 = \Delta z$

A similar approach with $(0, \Delta y)$ implies that $\overline{\Delta z } = -\Delta z$

Since limits are unique, these two approaches imply that

$\overline{z} + z = \overline{z} - z$ , which implies and cannot exist when

2

What does the sum below equal?

$\sum_{n=1}^{m}(e^{2\pi i/m})^{n}$

Another way of asking this question is what is the sum of the roots of unity.

$m\in \mathbb{N}$

$\pi$

$e^\pi$

Explanation

As messy as it looks, this is just a geometric series.

we will use the partial sum formula for the geometric series.

$S_{n}=\frac{a_{1}(1-r^n)}{1-r}$

$a_{1}=e^{2\pi i/m}$

$r=e^{2\pi i/m}$

$S_{m}=\frac{a_{1}(1-r^m)}{1-r}=\frac{e^{2\pi i/m}(1-{\color{Red} (e^{2\pi i/m})^m})}{1-e^{2\pi i/m}}$

the red part is the only part that matters....the cancel out leaving....

$S_{m}=\frac{a_{1}(1-r^m)}{1-r}=\frac{e^{2\pi i/m}(1-{\color{Red} (e^{2\pi i})})}{1-e^{2\pi i/m}}$

and...

$e^{2\pi i}=1$

thus we have...

$S_{m}=\frac{a_{1}(1-r^m)}{1-r}=\frac{e^{2\pi i/m}(1-{\color{Red} (1)})}{1-e^{2\pi i/m}}$

which gives the answer of zero.

$S_{m}=0$

Return to subject