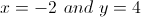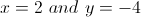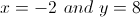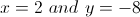Isolate in the first equation.

Plug into the second equation to solve for .

Plug into the first equation to solve for .

Now we have both the and values and can express them as a point: .

Substitute equation 2. into equation 1.,

so,

Substitute into equation 2:

so, the solution is .

We can evaluate the value of by subtracting the first equation from the second equation since both equations share , and can be eliminated.

The equation becomes:

Substitute this value back into either the first or second equation, and solve for y.

The answer is:

This problem is a system of equations, and uses the equation .

Start by assigning variables. Let stand for the rate of the boat, let stand for the rate of the current.

When the boat is going upstream, the total rate is equal to . You must subtract because the rates are working against each other—the boat is going slower than it would because it has to work against the current.

Using our upstream distance (400m) and time (2hr) from the question, we can set up our rate equation:

When the boat is going downstream, the total rate is equal to because the boat and current are working with each other, causing the boat to travel faster.

We can refer to the downstream distance (600m) and time (2hr) to set up the second equation:

From here, use elimination to solve for and .

1. Set up the system of equations, and solve for .

2. Subsitute into one of the equations to solve for .

In the second equation, you can substitute for from the first.

Now, substitute 2 for in the first equation:

The solution is

To solve by elimination, we want to cancel out either the or variable:

Now that we know the value of , we can plug it in to one of the equation sets to solve for :

We can then conclude that

Step 1: Set up the equations

Let = Nick's age now
Let = Sarah's age now

The first part of the question says "Nick's sister is three times as old as him". This means:

The second part of the equation says "in two years, she will be twice as old as he is then). This means:

Add 2 to each of the variables because each of them will be two years older than they are now.

Step 2: Solve the system of equations using substitution

Substitute for in the second equation. Solve for

Plug into the first equation to find

To solve this system of equations we must first eliminate one variable and solve for the remaining variable. We then substitute the variable back into our original equation and solve for the second variable still unknown.

We will use the elimination method:

Multiply the top equation by 1 and add it to the second equation:

--------------------------

Now we substitute the value of x into our original equation:

Thus, our lines are equal (intersect) at .

There are two ways to solve this:

-The 1st equation can be mutliplied by while the 2nd equation can be multiplied by and added to the 1st equation to make it a single variable equation where

.

This can be plugged into either equation to get

or

-The 2nd equation can be simplified to,

.

This value for can then be substituted into the first equation to make the equation single variable in .

Solving, gives , which can be plugged into either original equation to get

1st equation:

2nd equation:

Subtract the 2nd equation from the 1st equation to eliminate the "2y" from both equations and get an answer for x:

Plug the value of into either equation and solve for :