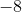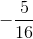Move to the other side by subtracting it from both sides.

Simplify:

Divide by the coefficient, the number in front of x.

Reduce:

To find this line, first find the slope (m) between the two coordinate points. Then use the point-slope formula to find a line with that same slope passing through a particular point.

Step 1: Subtract 6 from both sides...

Step 2: Divide by 2.

Simplify:

Upon solving for x, we find that x is less than or equal to 3. The left-hand term of the interval is negative infinity since any number less than 3 is in our set, and infinity always has a parenthesis around it. The right-hand term of the interval is 3 since it is the upper bound of our set. There is a bracket around it because 3 is included in our set (3 is less than or equal to 3). Remember when dividing or multiplying by a negative number in an inequality to reverse the direction of the inequality.

Add on both sides.

Add one on both sides.

Divide by 16 on both sides.

The answer is:

In order to isolate the x-variable, we will need to multiply both sides by one third.

Simplify both sides.

The answer is:

To solve, we must isolate x. In order to do that, we must first add 7 to both sides.

Next, we must divide both sides by 3.

First, we need to simplify what's inside the parentheses.

Now we continue to evaluate the left hand side.

The right hand side does not need any reduction.

We set the two sides equal to each other.

The first step is to distribute (multiply) the 2 through the parentheses:

Then isolate on the left side of the equation. Subtract the 10 from the left and right side.

Finally, to isolate , divide the left side by 2 so that the 2 cancels out. Then divide by 2 on the right side as well.

You can verify this answer by plugging the into the original equation.

First distribute out each side of the equation.

simplifies to .

Now for the right hand side,

becomes .

Now we equate both sides.

,