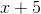We can accomplish this division by re-writing the problem as a fraction.

The denominator will distribute, allowing us to address each element separately.

Now we can cancel common factors to find our answer.

Divide the leading coefficients to get the first term of the quotient:

, the first term of the quotient

Multiply this term by the divisor, and subtract the product from the dividend:

Repeat these steps with the differences until the difference is an integer. As it turns out, we need to repeat only once:

, the second term of the quotient

, the remainder

Putting it all together, the quotient can be written as .

First, rewrite this problem so that the missing term is replaced by

Divide the leading coefficients:

, the first term of the quotient

Multiply this term by the divisor, and subtract the product from the dividend:

Repeat this process with each difference:

, the second term of the quotient

One more time:

, the third term of the quotient

, the remainder

The quotient is and the remainder is ; this can be rewritten as a quotient of

Determine if there are any common factors between the numerator and the denominator:

There are no common factors, so we use synthetic division to simplify the polynomial:

_________________

Bring down the 1, from the first column:

_________________

Multiply 1 by -1, and add the product to -3:

_________________

Multiply -4 by -1, and add the product to -10:

_________________

Solution: