Linear Motion - AP Physics C: Electricity and Magnetism

Card 1 of 286

0

Didn't Know

0

Didn't Know

Knew It

0

1 of 2019 left

Question

A guillotine blade weighing is accelerated upward into position at a rate of .

What is the the approximate mass of the guillotine blade?

Tap to reveal answer

Answer

The force of gravity on the blade is , which is the same as $400$\frac{kg\cdot $m}{s^2$}$$

This unit relationship comes from Newton's second law.

is the mathematical expression of Newton's second law. The units for force must be a product of the units for mass and the units for acceleration.

Solve the expression by plugging in known values.

$400 $\frac{kg\cdot $m}{s^2$}$=m \cdot $9.8$\frac{m}{s^2$}$$

$$\frac{400}{9.8}$kg=mass\approx41kg$

← Didn't Know|Knew It →

Question

A guillotine blade weighing is accelerated upward into position at a rate of .

What is the tension on the rope pulling the blade, while it is accelerating into position?

Tap to reveal answer

Answer

The tension in the rope is the sum of the forces acting on it. If one considers that the net force on an object must equal the mass of the object times the acceleration of the object, the net force on the object must be the force due to tension from the rope minus the force due to gravity.

Rearrange the equation.

Plug in known values.

$F_T=41kg\cdot2\frac ${m}{s^2$} + 400N$

← Didn't Know|Knew It →

Question

An object is moving in two dimensions. Its vertical motion relative to the horizontal motion is described by the equation $\small $y=ax^2$+bx +c$ . Its motion in the horizontal direction is described by the equation $\small $x=v_{x}$t$ . What is the object's velocity is the direction in terms of its horizontal position $\small x$ ?

Tap to reveal answer

Answer

The y velocity is thetime derivative of the $\small y$ position, and not the $\small x$ derivative. In order to find it, use the chain rule:

$\frac{dy}{dt}$=\left($\frac{dy}{dx}$\right) $\frac{dx}{dt}$

$$\frac{dy}{dx}$= 2ax + b$

Of course, $\frac{dx}{dt}$ $=v_{x}$

← Didn't Know|Knew It →

Question

Two objects moving in one dimension created the following velocity vs. time graph:

From the graph above, what is true about the two objects at time $\small t=5s$ ?

Tap to reveal answer

Answer

Since this is a graph of velocity and not position, the curves intersect where the velocities match. Since we do not know the starting position, we do not know where the objects are relative to one another.

← Didn't Know|Knew It →

Question

Two objects moving in one dimension created the following velocity vs. time graph:

From the graph above, which object has traveled a greater distance from its starting position when $\small t=5s$ ?

Tap to reveal answer

Answer

Since this is a graph of velocity vs. time, its integral is distance travelled. We can estimate the integral by looking at the area under the curves. Since Bbject 1 has a greater area under its velocity curve, it has covered a greater distance. Its velocity is greater that Object 2's for the entire time, so it makes sense that it will travel farther.

← Didn't Know|Knew It →

Question

Atwood's machine consists of two blocks connected by a string connected over a
pulley as shown. What is the acceleration of the blocks if their masses are and .

Assume the pulley has negligible mass and friction.

Tap to reveal answer

Answer

From the force diagram above, we can see that tension is pulling up on both sides of the string and gravity is pulling down on both blocks. With this information we can write 2 force equations:

If we add the two equations together, we get:

where

Solving for , we get

← Didn't Know|Knew It →

Question

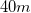A $\small 200g$ ball is thrown horizontally from the top of a $\small 40m$ high building. It has an initial velocity of 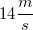$\small 14$\frac{m}{s}$$ and lands on the ground $\small 40m$ away from the base of the building. Assuming air resistance is negligible, which of the following changes would cause the range of this projectile to increase?

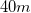
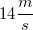
I. Increasing the initial horizontal velocity

II. Decreasing the mass of the ball

III. Throwing the ball from an identical building on the moon

Tap to reveal answer

Answer

Relevant equations:

$y_f - y_o = $v_{oy}$t +\frac{1}{2}$a_$yt^2$$

$R_x = $v_{ox}$t$

Choice I is true because is proportional to the range , so increasing increases if $\small t$ is constant. This relationship is given by the equation:

$R_x = $v_{ox}$t$

Choice II is false because the motion of a projectile is independent of mass.

Choice III is true because the vertical acceleration on the moon would be less. Decreasing 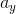increases the time the ball is in the air, thereby increasing if is constant. This relationship is also shown in the equation:

$R_x = $v_{ox}$t$

← Didn't Know|Knew It →

Question

Water emerges horizontally from a hole in a tank 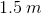above the ground. If the water hits the ground 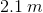from the base of the tank, at what speed is the water emerging from the hole? (Hint: Treat the water droplets as projectiles.)

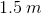
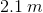
Tap to reveal answer

Answer

To understand this problem, we have to understand that the water has a x-velocity and a y-veloctiy. The x-velocity never changes.

First we want to find the time it took for the water to hit the ground. We can use this equation: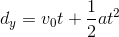 $d_y = v_0t + $$\frac{1}{2}$at^2$$

We know that the y-velocity is 0 to start with, acceleration is and .

Substituting into the equation, we get:

$1.5 = $$\frac{1}{2}$(9.8)t^2$\ \ t = $\sqrt{\frac{1.5}{0.5\cdot9.8}$}, t = 0.55:\up$\text{s}$$

Next we have to substitute the time into the equation for the x component

We know that and 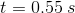, so we can conclude that:

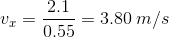
$v_x = $\frac{2.1}{0.55}$ = 3.80:m/s$

← Didn't Know|Knew It →

Question

An object starts from rest and reaches a velocity of $10$\frac{m}{s}$$ after accelerating at a constant rate for four seconds. What is the distance traveled in this time?

Tap to reveal answer

Answer

Since the acceleration is constant in this problem, we can apply the kinematics given equation to calculate the distance:

$\Delta x=v_$ot+\frac{1}{2}$at^2$$

First, we need to calculate the acceleration.

$a=\frac{\Delta v}{t}$=\frac{v-v_o}{t}$$

Plug in our velocity and time values to find the acceleration.

Now we can return to the kinematics equation and solve for the distance traveled:

$\Delta $x=(0$\frac{m}{s}$)(4s)+\frac{1}{2}$(2.5$\frac{m}{s^2$$}$)(4s)^2$$

$\Delta x=20m$

← Didn't Know|Knew It →

Question

At the moment a car is passed by another car constantly traveling at $10$\frac{m}{s}$$ , it begins to accelerate at . In how many seconds does this car catch up to and pass the other car?

Tap to reveal answer

Answer

First, find the displacement equations for both cars. Car 1 will be the car that is initially stationary; car 2 will be the car traveling with constant velocity.

Car 1:

$v_1(t) = \int a_1(t) dt = 5t$

$x_1(t) = \int v_1(t)dt = $2.5t^2$$

Car 2:

$x_2(t) = \int v_2(t)dt = 10t$

Now, set those displacement equations equal to each other and solve for .

The accelerating car will catch and pass the car traveling at constant velocity after 4 seconds.

← Didn't Know|Knew It →

Question

An object moving along a line has a displacement equation of , where is in seconds. For what value of is the object stationary?

Tap to reveal answer

Answer

Use the fact that to find the velocity equation, and then solve for when .

Take the derivative of the displacement equation.

Set the velocity equal to zero.

Solve for the time.

$t = $\frac{40}{10}$ = 4s$

← Didn't Know|Knew It →

Question

An object is moving on a line and has displacement equation of , where is in seconds. At what value of is the object not accelerating?

Tap to reveal answer

Answer

Take the second derivative of , to find the acceleration function . Then find the value of where . The fact that it is simply and not or inside that quantity means that using the Chain Rule becomes decidedly easier.

Set the acceleration fuction equal to zero and solve for the time.

← Didn't Know|Knew It →

Question

A projectile is launched out of a cannon or launch tube with zero air resistance or friction. At what angle (in degrees) should the projectile be launched to maximize the distance it travels?

Tap to reveal answer

Answer

The projectile travels the farthest when the vertical component of its velocity matches the sum of its horizontal component and whatever the wind/friction adds or subtracts. If the wind has no effect, then a 45-degree angle will be the best because the horizontal and vertical components of the velocity will create a right isosceles triangle (remember special triangles).

← Didn't Know|Knew It →

Question

A car undergoes acceleration according to the given function. What distance has the car traveled after three seconds?

Tap to reveal answer

Answer

We can determine the velocity by taking the second integral of acceleration for the time interval of 0s to 3s.

$\int a(t)dt = v(t)$

$\int_${0}^{3}$\int $a(t)dt^2$ = x(3) - x(0)$

Solve for the first integral.

$\int_${0}^{3}$\int $a(t)dt^2$ =\int_${0}^{3}$$(6t^2$)\int $dt^2$=\int_${0}^{3}$$(2t^3$)dt$

Solve for the second integral, using the time interval.

$\int_${0}^{3}$$(2t^3$)dt = $$\frac{(3)^4$$}{2}$-$\frac{(0)^4$}{2}$ = $\frac{81}{2}$ = 40.5m$

← Didn't Know|Knew It →

Question

A car undergoes acceleration according to the given function. How fast is the car moving after four seconds?

Tap to reveal answer

Answer

We can find the car's velocity by taking the integral of the acceleration function during the given time interval.

$v(t) = \int a(t),dt$

$v(4) = \int_${0}^{4}$ a(t),dt = \int_${0}^{4}$ $(6t^2$),dt$

Solve the integral for the time interval of 0s to 4s. This will give us the final velocity.

$\int_${0}^{4}$ $(6t^2$),dt = $2(4)^3$$+2(0)^3$ = 128\ $\frac{m}{s}$$

← Didn't Know|Knew It →

Question

A car undergoes acceleration according to the given function. If the threshold for serious injury or fatality for a human undergoing horizontal acceleration is 60 g ees (1 gee = 10 meters per second per second), how long would a human be able to withstand riding in this car?

Tap to reveal answer

Answer

Calculate the maximum acceration in meters per second.

$a(t) = $6t^2$ = 60\ gees = 600\ $$\frac{m}{s^2$}$$

Solve for the time.

$t = 10\ s$

← Didn't Know|Knew It →

Question

A ball travels with a velocity as described by the function below:

What is the ball's acceleration?

Tap to reveal answer

Answer

Acceleration is equal to the derivative of the velocity function.

$a(t) = $\frac{dv(t)}{dt}$$

Since the velocity is constant, the derivative will be equal to zero.

$$\frac{d}{dt}$(5) = 0$

The acceleration is equal to zero.

← Didn't Know|Knew It →

Question

A man runs with a velocity described by the function below.

What is the function for his acceleration?

Tap to reveal answer

Answer

The function for acceleration is the derivative of the function for velocity.

$a(t)= $\frac{dv(t)}{dt}$$

← Didn't Know|Knew It →

Question

A man runs with a velocity as described by the function below.

How far does he travel in 1 minute?

Tap to reveal answer

Answer

Distance is given by the integral of a velocity function. For this question, we will need to integrate over the interval of 0s to 60s.

$x(t) = \int_${0}^{60}$v(t),dt$

$x(60)=\int_${0}^{60}$(8t+4),dt = $(4(60)^2$$+4(60))-(4(0)^2$+4(0))$

$x(60)=4(3600)+240 = 14640\ m$

← Didn't Know|Knew It →

Question

A particle traveling in a straight line accelerates uniformly from rest to $50:\up$\text{cm/s}$$ in $5:\up$\text{s}$$ and then continues at constant speed for an additional for an additional $3:\up$\text{s}$$ . What is the total distance traveled by the particle during the $8:\up$\text{s}$$ ?

Tap to reveal answer

Answer

First off we have to convert $50:\up$\text{cm/s}$$ to meters per second.

$\frac{50:\uptext{cm}$}{s} \cdot $\frac{1:\uptext{m}$}{100\up$\text{cm}$} = 0.5:\up$\text{m/s}$

Next we have to calculate the distance the object traveled the first 5 seconds, when it was starting from rest. We are given time, initial speed to be . The acceleration of the object at this time can be calculated using:

, substituting the values, we get:

$0.5:\up$\text{m/s}$ = a(5s), a = $0.1:m/s^2$$

Next, we use the distance equation to find the distance in the first 5 seconds:

$x_1 = v_0t + $$\frac{1}{2}$at^2$$

because the initial speed is .

If we plug in , , we get: $x_1 = 1.25:\up$\text{m}$$

Next we have to find the distance the the object travels at constant speed for 3 seconds. We can use the equation:

in this case is not equal to , it is equal to $0.5:\up$\text{m}$$ and $t=3:\up$\text{s}$$

Plugging in the equation, we get

Adding and we get the total distance to be $2.75:\up$\text{m}$$

← Didn't Know|Knew It →

0

Knew It