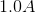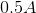AP Physics 2 - Ohm's Law

You have a circuit with a $5\Omega$ resistor connected to a battery. What is the current through the resistor?

Explanation

To find the current in a circuit with a battery and resistor(s), you use Ohm's Law.

$I=\frac{V}{R}$

We have the voltage and we have the resistance, so we don't need to rearrange the equation.

$I=\frac{10}{5}$

Therefore, the current through the resistor is 2 amps ().

Combined circuit

$R_1=R_3=R_4= 3\Omega$

$R_2=6\Omega$

In the circuit above, find the current through .

$\frac{3}{4}A$

None of these

$\frac{9}{8}A$

$\frac{27}{8}A$

Explanation

First, find the total resistance of the circuit.

and are in parallel, so we find their equivalent resistance by using the following formula:

$\frac{1}{R_{1}}+\frac{1}R_{2}=\frac{1}{R_{1+2}}$

$\frac{1}{3}+\frac{1}{6}=\frac{1}{R_{1+2}}$

$\frac{3}{6}=\frac{1}{R_{1+2}}}$

$R_{1+2}=2\Omega$

Next, add the series resistors together.

$R_{1+2}+R_3+R_4=R_{total}$

$R_{total}=8\Omega$

Use Ohm's law to find the current in the system.

$9V=I\cdot 8\Omega$

$I=\frac{9}{8}A$

The current through and needs to add up to the total current, since they are in parallel.

$I_1 + I_2 =I_{total}$

$I_1 + I_2 =\frac{9}{8}A$

Also, the voltage drop across them need to be equal, since they are in parallel.

$I_1\cdot3\Omega=I_2\cdot 6\Omega$

Set up a system of equations.

$I_1\cdot3\Omega=I_2\cdot 6\Omega$

$I_1 + I_2 =\frac{9}{8}A$

Solve.

$1.5I_1=\frac{9}{8}A$

$I_1=\frac{3}{4}A$

Combined circuit

$R_1=R_3=R_4= 3\Omega$

$R_2=6\Omega$

In the circuit above, find the voltage drop across .

$\frac{9}{4}V$

None of these

$\frac{9}{8}V$

Explanation

First, find the total resistance of the circuit.

and are in parallel, so we find their equivalent resistance by using the following formula:

$\frac{1}{R_{1}}+\frac{1}R_{2}=\frac{1}{R_{1+2}}$

$\frac{1}{3}+\frac{1}{6}=\frac{1}{R_{1+2}}$

$\frac{3}{6}=\frac{1}{R_{1+2}}}$

$R_{1+2}=2\Omega$

Next, add the series resistors together.

$R_{1+2}+R_3+R_4=R_{total}$

$R_{total}=8\Omega$

Use Ohm's law to find the current in the system.

$9V=I\cdot 8\Omega$

$I=\frac{9}{8}A$

and will have the same voltage drop across them, as they are in parallel, and are equivalent to the combined resistor $R_{1+2}$

$V=\frac{9}{8}A\cdot R_{1+2}$

$V=\frac{9}{8}A\cdot 2\Omega$

$V=\frac{9}{4}V$

Combined circuit

$R_1=R_3=R4= 3\Omega$

$R_2=6\Omega$

In the circuit above, find the voltage drop across .

$\frac{27}{8}V$

None of these

Explanation

First, find the total resistance of the circuit.

and are in parallel, so we find their equivalent resistance by using the following formula:

$\frac{1}{R_{1}}+\frac{1}R_{2}=\frac{1}{R_{1+2}}$

$\frac{1}{3}+\frac{1}{6}=\frac{1}{R_{1+2}}$

$\frac{3}{6}=\frac{1}{R_{1+2}}}$

$R_{1+2}=2\Omega$

Next, add the series resistors together.

$R_{1+2}+R_3+R_4=R_{total}$

$R_{total}=8\Omega$

Use Ohm's law to find the current in the system.

$9V=I\cdot 8\Omega$

$I=\frac{9}{8}A$

and will have the same voltage drop across them, as they are in parallel, and are equivalent to the combined resistor $R_{1+2}$

$V=\frac{9}{8}A\cdot R_{3}$

$V=\frac{9}{8}A\cdot 3\Omega$

$V=\frac{27}{8}V$

Three parallel resistors

What is the total resistance of the circuit?

$\frac{67}{13}\Omega$

None of these

$\frac{13}{15}\Omega$

$17\Omega$

$4\Omega$

Explanation

, , and are in parallel, so we add them by using:

$\frac{1}{R_1} + \frac{1}{R_2} + \frac{1}{R_3} = \frac{1}{R_{1,2,3}}}$

We find that $R_{1,2,3} = \frac{15}{13}\Omega$

$R_{1,2,3}$ , , and are in series. So we use:

$R_{1,2,3}+R_4 +R_5 = R_{total}$

$\frac{15}{13}\Omega+1\Omega +1\Omega = R_{total}$

$R_{total}=\frac{67}{13}\Omega$

Three parallel resistors

$R_1=R_4=R_5=2\Omega$

$R_2=5\Omega$

$R_3=6\Omega$

What is the current flowing through ?

None of these

Explanation

, , and are in parallel, so we add them by using:

$\frac{1}{R_1} + \frac{1}{R_2} + \frac{1}{R_3} = \frac{1}{R_{1,2,3}}}$

We find that $R_{1,2,3} = \frac{15}{13}\Omega$

$R_{1,2,3}$ , , and are in series. So we use:

$R_{1,2,3}+R_4 +R_5 = R_{total}$

$\frac{15}{13}\Omega+1\Omega +1\Omega = R_{total}$

$R_{total}=\frac{67}{13}\Omega$

First, we need to find the total current of the circuit, we simply use:

$I=\frac{V}{R}$

$I=\frac{15V}{\frac{67}{13}\Omega}$

$I=\frac{195}{67} amps$

Because , and are in parallel,

$I_1+I_2+I_3=I_{total}$

Also, the voltage drop must be the same across all three

Using

Using algebraic subsitution we get:

$I_3+I_3 \frac{R_3}{R_1}+I_3 \frac{R_3}{R_2}=I_{total}$

Solving for

$\frac{I_{Total}}{1+\frac{R_3}{R_1}+\frac{R_3}{R_2}}=I_3$

$\frac{I_{Total}}{1+\frac{6}{2}+\frac{6}{5}}=I_3$

A $9\textup{ V}$ battery is placed in series with five $9\ \Omega$ resistors. Find the current.

$.2\textup{ A}$

$3\textup{ A}$

$45\textup{ A}$

$9\textup{ A}$

$1\textup{ A}$

Explanation

In series, resistance adds conventionally.

$5*9\Omega=45\Omega$

Using

Three parallel resistors

What is the current flowing through ?

$\frac{195}{67} amps$

None of these

$\frac{67}{195} amps$

Explanation

, , and are in parallel, so we add them by using:

$\frac{1}{R_1} + \frac{1}{R_2} + \frac{1}{R_3} = \frac{1}{R_{1,2,3}}}$

We find that $R_{1,2,3} = \frac{15}{13}\Omega$

$R_{1,2,3}$ , , and are in series. So we use:

$R_{1,2,3}+R_4 +R_5 = R_{total}$

$\frac{15}{13}\Omega+1\Omega +1\Omega = R_{total}$

$R_{total}=\frac{67}{13}\Omega$

We will then find the total current of the circuit. This will also be the current of because this resistor is not in parallel with any others.

$I=\frac{V}{R}$

$I=\frac{15V}{(67/13)\Omega}$

$I=\frac{195}{67} amps$

A $9\textup{ V}$ battery is placed in series with five $9\ \Omega$ resistors. Find the voltage drop across each resistor.

$1.8\textup{ V}$

$3.6\textup{ V}$

$6\textup{ V}$

$10\textup{ V}$

$9\textup{ V}$

Explanation

In series, resistance adds conventionally.

$5*9\Omega=45\Omega$

Using Ohm's law for total current:

Now use Ohm's law for an individual resistor:

Three parallel resistors

$R_1=R_4=R_5=2\Omega$

$R2=5\Omega$

$R_3=6 \Omega$

What is the current flowing through ?

None of these

Impossible to determine

Explanation

, , and are in parallel, so we add them by using:

$\frac{1}{R_1} + \frac{1}{R_2} + \frac{1}{R_3} = \frac{1}{R_{1,2,3}}}$

We find that $R_{1,2,3} = \frac{15}{13}\Omega$

$R_{1,2,3}$ , , and are in series. So we use:

$R_{1,2,3}+R_4 +R_5 = R_{total}$

$\frac{15}{13}\Omega+1\Omega +1\Omega = R_{total}$

$R_{total}=\frac{67}{13}\Omega$

First, we need to find the total current of the circuit, we simply use:

$I=\frac{V}{R}$

$I=\frac{15V}{\frac{67}{13}\Omega}$

$I=\frac{195}{67} amps$

Because , and are in parallel,

$I_1+I_2+I_3=I_{total}$

Also, the voltage drop must be the same across all three

Using

Using algebraic subsitution we get:

$I_1+I_1 \frac{R_1}{R_2}+I_1 \frac{R_1}{R_3}=I_{total}$

Solving for

$\frac{I_{Total}}{1+\frac{R_1}{R_2}+\frac{R_1}{R_3}}=I_1$

$\frac{195/67}{1+\frac{2}{5}+\frac{2}{6}}=I_1$

Ohm's Law

Help Questions

Explanation

Explanation

Explanation

Explanation

Explanation

Explanation

Explanation

Explanation

Explanation

Explanation