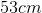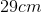AP Physics 1 - Torque | Practice Hub

Terry is pushing a vertical lever that is attached to the floor, and he pushes above the point of rotation. If he pushes with a force of at an angle of $60^{\text o}$ from the ground, what is the magnitude of torque that he is applying to the lever's hinge?

Explanation

Magnitude of torque can be found by relating the amount of force applied perpendicular to a lever arm about a point of rotation.

$\tau=rF$

In this case, the force is not perpendicular, so we must take the perpendicular aspect of the force to find torque.

$\tau=rFsin\theta$

Plug in and solve.

$\tau=1.5m(100N)sin(30^{\text o})$

$\tau=75Nm$

A symmetrical rectangle (, ) has four forces, all of the same magnitude, pulling at each corner as shown in the picture. Which of the following statements is true?

Net torque is not zero, but the net force is zero

Net force is not zero, but the net torque is zero

Both net torque and net force is zero

Neither net force nor net torque is zero

Explanation

First let's go on and define each of these terms...

Force: influence exerted

Torque: a way for us to measure of the effectiveness of a force which consists of a force and its perpendicular distance from the line of action amongst the axis of rotation

Each reference in which you find these definition may vary, but they should all have a common gist. Force is some type of implication on an object that can cause that object's mobility. Torque, however, is the capability of a specific force to create rotation. Therefore, torque is not a force, it's a characteristic of a force.

The forces shown in the diagram each have a reciprocal. In other words, $F_{1}$ is countered by $F_{3}$ , as $F_{2}$ is countered by $F_{4}$ . They each are equal, pulling in an opposite direction. With that said, the net force is zero. How? Well if we had a magazine (rectangle) and you and three of your friends each pulled on a corner as shown in the picture, the magazine wouldn't move. If you and a friend pulled on the same corners as $F_{1}$ and $F_{3}$ ,the magazine still wouldn't move (same goes for $F_{2}$ and $F_{4}$ ).

However, torques are slightly different. Torque is not (+) or (-), it is measured as clockwise or counter clockwise. So, looking at our diagram, all of the forces are in the same direction around the central pivot point (black circle). If three out of four of the forces shown were taken away, any of the remaining would cause the rectangle to rotate in the same manner (counter clockwise) around the pivot point. Therefore the net torque, or the total of the torques are all in the same direction and will NOT have a net value of zero, but rather a grand total of each force's torque separately.

A simple pendulum with length $L = 4\textup{ m}$ with a block of mass $m = 2\textup{ kg}$ attached to one end is initially at rest in the horizontal position. At time , the pendulum is released and allowed to rotate freely. What is the torque torque applied on the pendulum at $t = 2\textup{ s}$ ?

$g = 10\ \frac{\textup{m}}{\textup{s}^2}$

$80\textup{ N}\cdot \textup{m}$

$66\textup{ N}\cdot \textup{m}$

$37\textup{ N}\cdot \textup{m}$

$30\textup{ N}\cdot \textup{m}$

$18\textup{ N}\cdot \textup{m}$

Explanation

To calculate the torque on the pendulum, we need to know the position of the pendulum. We can find this using the following expression:

$\theta = \theta _{max}cos\left ( \sqrt{\frac{L}{g}}t\right )$

Note that we are using the cosine function because the pendulum begins at it's maximum angle. Plugging in our values:

$\theta =90^{\circ}cos\left ( \sqrt{\frac{(4m)}{\left ( 10\frac{m}{s^2}\right )}}(2s)\right )$

$\theta = 90^{\circ}$

The pendulum is still horizontal, but now on the other side. Now we can directly calculate the torque placed on the pendulum

$\tau = F\cdot r$

Where the radius is the length of the pendulum and the force is the weight of the block (since the pendulum is horizontal).

$\tau = mgL$

$\tau = (2kg)\left ( 10\frac{m}{s^2}\right )(4m)$

$\tau = 80N\cdot m$

Two masses hang below a massless meter stick. Mass 1 is located at the 10cm mark with a weight of 15kg, while mass 2 is located at the 60cm mark with a weight of 30kg. At what point in between the two masses must the string be attached in order to balance the system?

Explanation

This problem deals with torque and equilibrium. Noting that the string is between the two masses we can use the torque equation of $\tau_{ccw} = \tau _{cw}$ . We can use the equation $\tau = rFsin\theta$ to find the torque. Since force is perpendicular to the distance we can use the equation $\tau = rF$ (sine of 90o is 1). Force presented in this situation is gravity, therefore F=mg, and using the variable x as a placement for the string we can find r.

$\tau_{ccw} = \tau _{cw}$

$r_{1} (M_1) = r_{2}(M_2)$

x=43, thus the string is placed at the 43cm mark.

Marc, Paul, and David all apply forces to a pendulum consisting of a rigid rod. Marc applies a force a distance from the pivot. If David applies a force of a distance $\frac{d}{2}$ from the pivot in the same direction as Marc, how much force must Paul apply in the opposite direction a distance of from the pivot if he is to make the sum of the torques about the pivot equal zero? Assume all three apply forces perpendicular to the rod.

$\frac{5}{4}F$

$\frac{5}{2}F$

$\frac{F}{2}$

$\frac{2}{5}F$

Explanation

First, we must recall the formula for torque, which is

$\tau=rFcos\theta$

is the distance from the pivot, called the moment arm. is the force, and $\theta$ is the angle relative to the normal of the object.) Since all the forces are being applied perpendicular to the surface of the rod, $\theta=0$ . Thus,

$\tau =rF$

The sum of the torques must equal zero, so David's torque plus Marc's torque must be the same as Paul's torque because David and Marc are applying torques in the opposite direction as Paul. This gives us

$\left(\frac{d}{2}\right)(3F)+dF=2d(F_{p})$

$\frac{5dF}{2}=2dF_{p}$

Dividing both sides by , we get Paul's force $(F_{p})$ to be $\frac{5}{4}F$

of force is applied perpendicular to a wrench. Calculate the torque generated.

$22.5N\cdot m$

None of these

$31.3N\cdot m$

$18.7N\cdot m$

$2250N\cdot m$

Explanation

$\tau=F\times d$

$\tau=|F||d|sin\theta$

Converting to and plugging in values

$\tau=|150||.15|sin90^\circ$

$\tau=22.5N\cdot m$

A bolt connecting the main and rear frame of a mountain bike requires a torque of $15N\cdot m$ to tighten. If you are capable of applying of force to a wrench in any given direction, what is the minimum length of the wrench that will result in the required torque?

Explanation

The minimum length of the wrench will assume that the maximum force is applied at an angle of $90^{\circ}$ . Therefore, we can use the simplified expression for torque:

$T = F\cdot r$

Here, is the length of the wrench.

Rearranging for length and plugging in our values, we get:

$r = \frac{T}{F}=\frac{15N\cdot m}{40N} = 0.375 m$

A 3m beam of negligible weight is balancing in equilibrium with a fulcrum placed 1m from it's left end. If a force of 50N is applied on it's right end, how much force would needs to be applied to the left end?

Explanation

This a an example of rotational equilibrium involving torque. The formula for torque is $\tau = Fdsin\left ( \Theta \right )$ , where $\Theta$ is the angle that the force vector makes with the object in equilibrium and is the distance from the fulcrum to the point of the force vector. To achieve equilibrium, our torques must be equal.

$F_1d_1sin(\Theta_1)=F_2d_2sin(\Theta_2)$

Since the forces are applied perpendicular to the beam, $sin(\Theta)$ becomes 1. The distance of the fulcrum from the left end is 1m and its distance from the right end is 2m.

$\frac{(50N)(2m)}{1m}=100N=x$

Since the 50N force is twice as far from the fulcrum as the force that must be applied on the left side, it must be half as strong as the force on the left. The force on the left can be found to be 100N.

There is a weight to the left the center of a seesaw. What distance from the center on the right side of the seesaw should Bob sit so that the seesaw is balanced?

Bob's mass is

$g = 10 \frac{m}{s^2}$

Explanation

Torque is defined as $\tau = rFsin\Theta$ . In this case, $\Theta$ is zero because Bob and the weight are sitting directly on top of the seesaw; all of their weight is projected directly downward. Therefore, the torque that the weight applies is:

$\tau_{weight} = 3m\cdot(100kg\cdot10\frac{m}{s^2})=3000N$

In order for the seesaw to balance, the torque applied by Bob must be equal to .

$3000N=r\cdot(60kg\cdot10\frac{m}{s^2})$

Michael just created a large square pinwheel. He attaches his pinwheel to a pivot screw in the middle of the square (side = ) allowing it to spin in the wind. However, when he brings it outside, the pinwheel doesn't move. Frustrated, Michael gives the bottom corner a flick (). What is the torque of the force provided?

Explanation

It is important to remember that torque is not a force, it's a characteristic of a force.

$\tau = F \cdot r \cdot \sin \theta$

F is the force applied, r is the distance from the force's contact point and the object's center of mass, $\theta$ is the angle between and .

The trick to this problem is in two steps:

Find the using the Pythagorean theorem.
What's our $\theta$ ? Well we know that every square has 4 $90^{\circ}$ angles. If we drew a line from the corner of the square to the very middle (pivot point) of the pinwheel, we've just cut one of those angles in half! $\theta=45^{\circ}$