AP Physics 1 - Impulse and Momentum

A bullet weighing is fired at a velocity of $360\frac{m}{s}$ at a block weighing at rest on a frictionless surface. When the bullet hits the block, it becomes lodged in the block and causes the block to move. How fast does the block move after the collision?

$20.4 \frac{m}{s}$

$354 \frac{m}{s}$

$21.6\frac{m}{s}$

$4.52\frac{m}{s}$

$6.0\frac{m}{s}$

Explanation

Using the equation of momentum,

we can compare the initial and final scenarios and set them equal to each other to solve for the final velocity of the block (don't forget to convert the units of to !):

$m_{1}v_{1}=m_{2}v_{2}$

$.06\times360 = (.06+1)\times v_{2}$

$v_2\approx 20.4$

A object is moving along with the velocity given below. Calculate the magnitude of the momentum vector $\vec{p}$ .

$\vec{v}=5\hat{i}-2\hat{j}$

$162 kg\frac{m}{s}$

$90kg\frac{m}{s}$

$210kg\frac{m}{s}$

$58kg\frac{m}{s}$

$300kg\frac{m}{s}$

Explanation

We begin by writing down the definition of an object's linear momentum $\vec{p}$

$\vec{p}=m\vec{v}$

$\vec p=30kg\left(5\hat{i}-2\hat{j} \right )\frac{m}{s}$

$\vec p=\left( 150\hat{i}-60\hat{j}\right )kg\frac{m}{s}$

We then find the magnitude of the momentum by taking the square root of the sum of squares of its components.

$\left| \vec{p}\right| = \sqrt{p_x^2+p_y^2}$

$\left|\vec p\right|=\sqrt{150^2+60^2}kg\frac{m}{s}=162kg\frac{m}{s}$

A blue rubber ball weighing is rolling with a velocity of $2\frac{m}{s}$ when it hits a still red rubber ball with a weight of . After this elastic collision, what are the speeds and directions of the blue and red balls respectively?

$\frac{2}{3} \frac{m}{s}$ to the left, $\frac{4}{3} \frac{m}{s}$ to the right

$\frac{4}{3} \frac{m}{s}$ to the left, $\frac{2}{3} \frac{m}{s}$ to the right

$\frac{4}{3} \frac{m}{s}$ to the right, $\frac{2}{3} \frac{m}{s}$ to the left

At rest, $2 \frac{m}{s}$ to the right

At rest, $1 \frac{m}{s}$ to the right

Explanation

Because we are solving for two velocities (two unknowns), we need two equations. We can use the conservation of linear momentum:

$m_{1}v_{1}+m_{2}v_{2} = m_{1}v_{1}'+m_{2}v_{2}'$

Because we know that the collision is elastic, we know that kinetic energy is conserved:

$\frac{1}{2}m_{1}v_{1}^{2}+\frac{1}{2}m_{2}v_{2}^{2}=\frac{1}{2}m_{1}v_{1}'^{2}+\frac{1}{2}m_{2}v_{2}'^{2}$

The red ball starts at rest so

$v_{2}=0$

The above equations can then be simplified and one can solve for $v_{1}'$ and $v_{2}'$ .

$v_{1}'=\left ( \frac{m_{1}-m_{2}}{m_{1}+m_{2}} \right )v_{1}=\left ( \frac{20-40}{20+40} \right )2=-\frac{2}{3}$

Negative implies the ball is moving to the left.

$v_{2}'=\left ( \frac{2m_{1}}{m_{1}+m_{2}} \right )v_{1}=\left ( \frac{2(20)}{20+40} \right )2=\frac{4}{3}$

One car with a mass of 400kg is traveling east at $20\frac{m}{s}$ and collides with a car of mass 800kg traveling west at $15\frac{m}{s}$ . Assuming the collision is completely inellastic, what is velocity of the first car after the collision?

$3.33\frac{m}{s}\ \text{west}$

$3.33\frac{m}{s}\ \text{east}$

$1.0\frac{m}{s}\ \text{west}$

$1.0\frac{m}{s}\ \text{east}$

$0.0\frac{m}{s}$

Explanation

Since the collision is completely inelastic, momentum is conserved but energy is not. Furthermore, the two cars stick to each other and travel as one. The equation for conservation of momentum is as follows:

There are two inital masses with different velocities and one final mass with a single velocity. Therefore, we can write:

Rearranging for final velocity, we get:

$v = \frac{m_1v_1 + m_2v_2}{m}$

At this point, we can denote which direction is positive and which is negative. Since the car traveling west has more momentum, we will consider west to be positive. Substituting our values into the equation, we get:

$v = \frac{(400)(-20)+ (800)(15)}{400 + 800}$

$v = \frac{-800 + 12000}{1200} = \frac{4000}{1200} = 3.33\frac{m}{s}$

Since this value is positive, the final answer is $3.33\frac{m}{s}$ West.

A popular topic in early space exploration was how to safely return modules back to the surface of the earth. Early designs contained materials that could only withstand impulses of up to $4500 \frac{kg\cdot m}{s}$ before parts of the module became compromised. One such model of mass 500kg is approaching ocean waters and deploys its shoot, reducing its speed to $8 \frac{m}{s}$ . If the module decelerates to zero velocity in 0.9 seconds upon hitting the water, is the module structurally compromised?

$g=10\frac{m}{s^2}$

No; the impulse experienced is $4000\frac{kg\cdot m}{s}$

Yes; the impulse experienced is $4700\frac{kg\cdot m}{s}$

No; the impulse experienced is $3400\frac{kg\cdot m}{s}$

Yes; the impulse experienced is $5300\frac{kg\cdot m}{s}$

More information is needed to solve

Explanation

We need to use the equation for impulse to solve this problem. In fact, the time given is completely irrevelevant:

$I =F\cdot t = m \Delta v$

Plugging in our values:

$I = (500kg)(8\frac{m}{s}) = 4000 \frac{kg\cdot m}{s}$

This is less than the threshold, so no, nothing becomes structurally compromised

Which of the following explains why when we land on our feet, we instinctively bend our knees? Hint: think about the relationship between force, impulse, and time.

By bending our knees we extend the time it takes us to stop, which diminishes the impact force

By bending our knees we use a greater force to stop, which makes the impulse smaller

When we bend our knees we extend the time in which we apply the force that stops us, so our impulse is greater

When we bend our knees we extend the time in which we apply the force that stops us, so our impulse is smaller

By bending our knees we extend the time it takes us to stop, which increases the impact force

Explanation

Say that, when we hit the ground, we have a velocity , which is predetermined by whatever happens before the impact. When we hit the ground you will experience a force for some time. This force will cause the acceleration that reduces our velocity to zero and gets us to stop. Note that, regardless of how much time it takes us to stop, the change in momentum (impulse) is fixed, since it directly depends on how much our velocity changes:

$P_f=\frac{0kg\cdot m}{s}$ (since we come to a stop)

Note that the initial momentum does not depend on the impact force nor on how much time it takes to stop. The initial momentum depends on the velocity we have when we first hit the ground. This velocity is given by whatever happened before we hit the ground, which no longer concerns us since we only care about what happens from the moment we first hit the ground till the moment we stop. Yes, the time that passes for you to stop is very small, but it is impossible for it to be zero. So we have that the change in momentum (impulse) is a constant:

$\Delta P=-mv= constant$ , since is predetermined.

Remember that any change in momentum for a given mass occurs because its velocity changes. The velocity of the mass changes due to an acceleration and an acceleration is caused by a force. This gives us a relationship between force and impulse:

$F=\Delt\frac{\Delta P}{t}$

In our scenario, would be the impact force that stops us and the time it takes us to stop. From the equation above, it is easy to see that, since $\Delta P$ is fixed, when gets larger gets smaller, and the other way around. Therefore, we bend our knees to effectively increase the time it takes us to stop. Thus, diminishing the impact force as to avoid hurting ourselves.

Jennifer has a mass of . She is riding her skateboard east at $5\frac{m}{s}$ . She collides with Tommy, who is riding in the opposite direction at $4\frac{m}{s}$ . After they collide, they continue in Tommy's direction at $1\frac{m}{s}$ . Find the mass of Tommy.

Explanation

Using conservation of momentum

Solving for

$m_2=m_1\frac{(v_f-v_1_i)}{(v_2_i-v_f)}$

Plugging in values:

$m_2=70*\frac{(-1-5)}{(-4--1)}$

(A negative value is assumed for Tommy's direction for simplicity, a negative could have been used for Jennifer's instead, it will yield the same result.

A dump truck is traveling with a large load and a lot of momentum. The truck now travels faster, doubling its velocity. How does the momentum change after the truck doubles its velocity?

The momentum doubles

The momentum is zero

The momentum remains unchanged

The momentum quadruples

The momentum is halved

Explanation

Using the equation for momentum,

If the mass stays constant and the velocity doubles, the momentum must double as well to balance the equation.

Consider the following system:

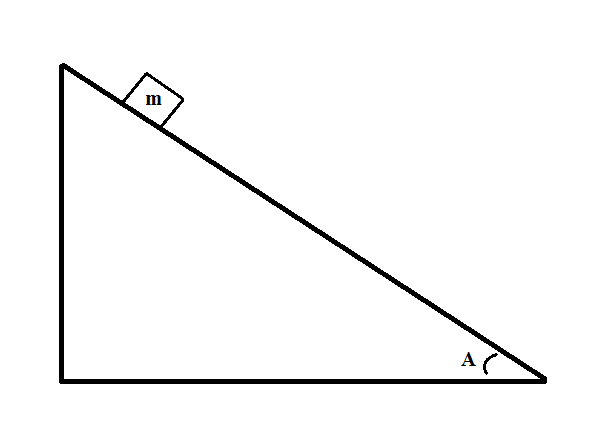
Slope_2

If the block has a mass of , the angle measures $50^{\circ}$ , and there is no friction between the block and slope, what is the momentum of the block after it has traveled a horizontal distance of ?

$309\frac{kg\cdot m}{s}$

$178\frac{kg\cdot m}{s}$

$54\frac{kg\cdot m}{s}$

$110\frac{kg\cdot m}{s}$

$550\frac{kg\cdot m}{s}$

Explanation

To calculate the momentum of the block, we first need to know the velocity of the block. This can be found using the equation for the conservation of momentum:

If we assume that the final height is zero, we can eliminate initial kinetic energy and final potential energy, getting:

Substituting expressions for each term, we get:

$mgh_i = \frac{1}{2}mv_f^2$

Cancel out mass and rearrange to solve for velocity:

$v_f = \sqrt{2gh_i} = \sqrt{2(10\frac{m}{s^2})(h_i)}$

We can use the horizontal distance traveled and the angle of the slope to determine the initial height:

$tan(A) = \frac{h_i}{horizontal}$

$h_i = tan(A)\cdot horizontal$

$h_i = tan(50^{\circ})*10m = 11.9m$

Now that we have the initial height, we can solve for final velocity:

$v_f = \sqrt{2(10\frac{m}{s^2})(11.9m)} = 15.4\frac{m}{s}$

Finally, we can now use the equation for momentum to solve the problem:

$p = m\Delta v$

$p = (20kg)(15.4\frac{m}{s})$

$p = 309 \frac{kg\cdot m}{s}$

A man is running at $2.1\frac{m}{s}$ . From that run, he jumps on a resting skateboard of mass of . Assuming no energy lost to friction, determine the final velocity of the man on the board.