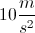AP Physics 1 - Fundamentals of Displacement, Velocity, and Acceleration

Given vector $\vec{A}$ has a magnitude of directed $35^{\circ}$ above the $+\hat{x}$ axis, and vector $\vec{B}$ has a magnitude of directed $70^{\circ}$ above the $+\hat{x}$ axis, calculate $\vec{A}\cdot \vec{B}$ .

Explanation

By definition, the dot product of two vectors can be related to their magnitudes and the angle between them as follows:

$\vec{A}\cdot\vec{B}=\left| \vec{A}\right| \left| \vec{B}\right|\cos{\theta}$

Given the angle between the two vectors is $\theta = 75^{\circ}-35^{\circ}=35^{\circ}$ , we can calculate the dot product to be written explicitly as:

$\vec{A}\cdot\vec{B}=5m \left( 8m\right)\cos{35^{\circ}}=32.8m^2$

Note that the unts are since the dot product involves multiplying two meters together.

A cannon is packed with gunpowder and a ball of mass 10kg. The cannon is angled at 30 degrees. When fired, the gunpowder releases 500J of energy, which is all transferred to the cannon ball. Neglecting air resistance and friction within the cannon, how far does the ball travel before hitting the ground?

Assume $g = 10\frac{m}{s^2}$

Explanation

There are two ways to solve this problem. The first and much easier way is to use the range equation. The second is using your kinematics equations.

Method 1: Range Equation

The range equation is the following:

$R = \frac{v_o^2sin(2\theta)}{g}$

We know everything ecvept for the initial velocity. However, we can calculate it knowing that the cannon transfers 500 J of energy to the ball. Therefore:

$K = 500 J = \frac{1}{2}mv^2$

Rearranging for velocity:

$v= \sqrt{\frac{2(500J)}{m}}= \sqrt{\frac{1000J}{10kg}} = 10\frac{m}{s}$

Now we can plug everything into the range equation:

$R = \frac{(10\frac{m}{s})^2sin(60^\circ)}{10\frac{m}{s^2}} = 8.7 \frac{m}{s}$

Method 2: Kinematics Equations

As in the first method, we can calculate the initial velocity of the ball:

$K = 500 J = \frac{1}{2}mv^2$

Rearranging for velocity:

$v= \sqrt{\frac{2(500J)}{m}}= \sqrt{\frac{1000J}{10kg}} = 10\frac{m}{s}$

We can then split this into it's components:

$v_{xi} = 10cos(30^{\circ}) = 8.66\frac{m}{s}$

$v_{yi} = 10sin(30^{\circ}) = 5\frac{m}{s}$

We can use the y-component to calculate how long the ball is in the air. We can do one of two things:

Calculate how long the ball takes to reach it's peak and then multiply by 2
Calculate how lon gthe ball takes to get a velocity of -5

We'll go with method 2:

Rearranging for t:

$t = \frac{v_f -v_i}{a} = \frac{-5\frac{m}{s^2}-5\frac{m}{s^2}}{-10\frac{m}{s^2}}$

Then we can multiply this time by the horizontal velocity (which stays constant because we are neglecting air resistance).

$x = v_x t = (8.66 \frac{m}{s})(1s) = 8.66 m$

The position of a particle can be described by:

The position is measured in , and the time is in . What is the average velocity for the particle in the time interval ?

$5 \frac{m}{s}$

$4 \frac{m}{s}$

$3 \frac{m}{s}$

$2 \frac{m}{s}$

$10 \frac{m}{s}$

Explanation

You can think of the average velocity of a particle as the difference between the final and initial states. Conventionally, we call this slope. Therefore, we need to plug in our two initial times into the position function, and use the equation for slope between two points to determine the average velocity.

Therefore, our two coordinates are:

Now, we use the slope equation:

$\frac{y_{2}-y_{1}}{x_{2}-x_{1}}=\frac{32-12}{4-0}=\frac{20}{4}=5\frac{m}{s}$

Imagine a decending elevator that is increasing it's speed. What is the direction of the acceleration of the elevator?

Down

Left

Right

Explanation

A trick that I often use is if something is speeding up, the acceleration and velocity point in the same direction. If something is slowing down. the acceleration and velocity point opposite directions. Since the elevator is speeding up, the acceleration must point in the same direction as it's velocity: downwards.

A box is placed on a 30o frictionless incline. What is the acceleration of the box as it slides down the incline?

$5\frac{m}{s^2}$

$10\frac{m}{s^2}$

$15\frac{m}{s^2}$

$3\frac{m}{s^2}$

$12\frac{m}{s^2}$

Explanation

To find the acceleration of the box traveling down the incline, the mass is not needed. Using the incline of the plane as the x-direction, we can see that there is no movement in the y-direction; therefore, we can use Newton's second, F = ma, in the x-direction.

There is only one force in the x-direction (gravity), however gravity is not just equal to “mg” in this case. Since the box is on an incline, the gravitational force will be equal to mgsin(30o). Substituting force into F =ma we find that mgsin(30o) = ma. We can now cancel out masses and solve for acceleration.

$F=ma\ and\ F=mgsin(\theta)$

$ma=mgsin(\theta)$

$ma=m(10\frac{m}{s^2})sin(30^o)=m(10\frac{m}{s^2})(0.5)$

$a=5\frac{m}{s^2}$

An object travels with a velocity for a period of time . Its velocity is instantaneously changed to a second velocity at which it travels for a period of time .

What is the correct expression for the object's average velocity during the entire two-part motion?

$\frac{(v_1t_1)+(v_2t_2)}{t_1+t_2}$

$\frac{(v_1t_1)(v_2t_2)}{t_1t_2}$

$\frac{(v_1+v_2)}{t_1+t_2}$

$\frac{(v_1t_1)+(v_2t_2)}{2}$

$\frac{(v_1)+(v_2)}{t_1-t_2}$

Explanation

Average velocity can be found by taking the total distance traveled in the two part motion and dividing by the total time of the two part motion as shown by the equation for velocity:

$v=\frac{\Delta x}{\Delta t}$

Where is velocity, is displacement, and is time.

Our average velocity then would be:

$v_a_v= \frac{x_1+x_2}{t_1+t_2}$

While we were not given the displacements for either part, we can solve for them by rearranging the velocity equation:

Substituting for the unknown displacements with equivalent terms comprised of the known velocities and times we find that the average velocity is:

$\frac{(v_1t_1)+(v_2t_2)}{t_1+t_2}$

A walker is walking at a constant rate of $1\frac{m}{s}$ on a circular track that is 400m in length. A runner is also on the track going in the same direction as the walker, running at an unknown constant speed. The runner and the walker are together, then meet each other again when the walker has completed $\frac{1}{2}$ of a lap, or 200m. What is the runner's speed?

$3.0\frac{m}{s}$

$2.0\frac{m}{s}$

$4.0\frac{m}{s}$

$3.5\frac{m}{s}$

$2.5\frac{m}{s}$

Explanation

The equation for speed is:

$speed=\frac{distance, traveled}{elapsed, time}$

The runner has gone around the track 1.5 times, thus his total distance traveled is:

We can find the elapsed time from the walker: Rearrange the speed equation to find time:
$elapsed,time=\frac{distance, traveled}{speed}=\frac{200m}{1\frac{m}{s}}=200s$

Now we have all the information we need to find the runner's speed:
$speed=\frac{distance, traveled}{elapsed, time}=\frac{600m}{200s}=3\frac{m}{s}$

A woman with a jet pack is above the ground. She drops a ball. If she waits until after she dropped the ball to accelerate downward to try and catch it, how fast will she have to accelerate to reach it at a height of ?

$108\frac{m}{s^2}$

$18.6\frac{m}{s^2}$

None of these

$254\frac{m}{s^2}$

$81\frac{m}{s^2}$

Explanation

Distance fallen by ball:

$.5at_{ball}^2=d_{ball}$

Distance fallen by woman:

$.5at_{woman}^2=d_{woman}$

Both distances need to be

If it fell

Since she waits to drop, $t_{ball}-2s=t_{woman}$

Combining equations:

$.5at_{ball}^2=d_{ball}$

Solving for $t_{ball}$

$t_{ball}=\sqrt{\frac{2*d_{ball}}{a}}$

Acceleration will be gravity

$t_{ball}=2.86s$

$t_{woman}=.86s$

$.5at_{woman}^2=d_{woman}$

$a_{woman}=108\frac{m}{s^2}$

A car is stopped at a red light. When the light turns green, it accelerates uniformly at a rate of $2 \frac{m}{s^{2}}$ . How fast is the car traveling after seconds?

$20 \frac{m}{s}$

$5 \frac{m}{s}$

$10 \frac{m}{s}$

$0.2 \frac{m}{s}$

$1 \frac{m}{s}$

Explanation

Acceleration is defined as a change in velocity over time:

$a = \frac{\Delta v}{t} = \frac{v_{f}-v_{i}}{t}$

Since the car is initially at rest at the stop light, $v_{i}=0$ . The acceleration is given as $2\frac{m}{s^{2}}$ and the problem is asking for the velocity at . Therefore,

$2\frac{m}{s^{2}} = \frac{\Delta v}{10s}$

$\Delta v=20\frac{m}{s}$

Two cars are racing side by side on a perfectly circular race track. The inner car is from the center of the track. The outer car is from center of the track.