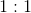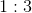AP Physics 1 - Coulomb's Law

An excess charge of is put on an ideal neutral conducting sphere with radius . What is the Coulomb force this excess charge exerts on a point charge of that is from the surface of the sphere?

$k=8.99*10^9\frac{m^2N}{C^2}$

Explanation

Two principal realizations help with solving this problem, both derived from Gauss’ law for electricity:

The excess charge on an ideal conducting sphere is uniformly distributed over its surface
A uniform shell of charge acts, in terms of electric force, as if all the charge were contained in a point charge at the sphere’s center

With these realizations, an application of Coulomb’s law answers the question. If $q_{2}$ is the point charge outside the sphere, then the force $F_{q2}$ on $q_{2}$ is:

$F_{q2} = \frac{kq_{sphere}q_{2}}{r^{2}}$

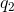
In this equation, is Coulomb’s constant, $q_{sphere}$ is the excess charge on the spherical conductor, and is total distance in meters of $q_{2}$ from the center of the conducting sphere.

Using the given values in this equation, we can calculate the generated force:

$F_{q2}=\frac{(8.99*10^9\frac{m^2N}{C^2})(10*10^{-6}C)(5*10^{-6}C)}{(0.5m)^2}$

$F_{q2}=\frac{0.4495m^2N}{0.25m^2}=1.798N$

Determine the strength of a force of proton on another proton in the nucleus if they are $10^{-15}m$ apart.

$k=8.99*10^9\frac{N}{m^2C^2}$

$e=1.602*10^{-19}C$

$230*10^{-15}N$

$230*10^{15}N$

Explanation

Use Coulomb's law:

$F_c=\frac{k*Q*q}{r^2}$ , where is Coulomb's constant, are charges of the two points and is the distance between the charges.

$F_c=\frac{8.99*10^9*(1.602*10^{-19})^2}{(10^{-15})^2}=230N$

Two protons are at a distance $r_{1}$ away from each other. There is a force $F_{1}$ acting on each proton due to the other. If the protons are moved so that they are now at a distance

$r_{2}=\frac{1}{2} r_{1}$ apart, what is the new force acting on each proton due to the other $\left (F_{2} \right )$ ?

$F_{2}=4 F_{1}$

$F_{2}=\frac{1}{2} F_{1}$

$F_{2}=2 F_{1}$

$F_{2}=\frac{1}{4} F_{1}$

Explanation

Coulomb's law shows that the force between two charged particles is inversely proportional to the square of the distance between the particles.

$F=k \frac{q_{1}q_{2}}{r^{2}}$

If the distance between the charges is reduced by $\frac{1}{2}$ , that means the $\frac{1}{2}$ is squared in the denominator and the will flip up to the top to give time the original force. More explicitly, if we plug in the given information the initial force will be:

$F_{1}=k \frac{q_{1}q_{2}}\left ( {r_{1}\right )^{2}}$

$F_{2}=k \frac{q_{1}q_{2}}\left ( {r_{2}\right )^{2}}=k \frac{q_{1}q_{2}}\left ( \frac{1}{2}{r_{1}\right )^{2}}$

$F_{2}=k \frac{q_{1}q_{2}}{ \frac{1}{4}\left (r_{1}\right )^{2}}=4 k \frac{q_{1}q_{2}}{\left (r_{1}\right )^{2}}$

$F_{2}=4 F_{1}$

If we have 2 charges, and , that are apart, what is the force exerted on by if we know that has a charge of $-13\mu C$ and has a charge of $-12\mu C$ ?

Explanation

Use Coulomb's law.

$F=\frac{kq_1q_2}{r^2}$

Plug in known values and solve.

$F=\frac{(9\cdot10^{9})(-12\cdot10^{-6})(-13\cdot10^{-6})}{(0.14^{2})}$

Note that this force is positive, which means it's repulsive.

If we have 2 charges, and , that are apart, what is the force exerted on by if we know that has a charge of $15\mu C$ and has a charge of $15\mu C$ ?

Explanation

Use Coulomb's law.

$F=\frac{kq_1q_2}{r^2}$

Plug in known values and solve.

$F=\frac{(9\cdot10^{9})(15\cdot10^{-6})(15\cdot10^{-6})}{(0.15^{2})}$

Note that the force between two charges of the same sign (both positive or both negative) is positive. This indicates the force is repulsive, which makes sense since both charges are positive.

Charges A and B are placed a distance of from one another. The charge of particle A is whereas the charge of particle B is . Charge B experiences an electrostatic force of from charge A. Similarly, charge A experiences an electrostatic force of from charge B.

What is the ratio of to ?

Explanation

This question is very simple if you realize that the force experienced by both charges is equal.

The definition of the two electrostatic forces are given by Coulomb's law:

$F=-k\frac{q_1q_2}{r^2}$

In this question, we can rewrite this equation in terms of our given system.

$F_a = -k\frac{q_a q_b}{r^2}=-k\frac{(0.003C)(0.006C)}{(1.5m)^2}=-k(8*10^{-6}\frac{C^2}{m^2})$

$F_b = -k\frac{q_b q_a}{r^2}=-k\frac{(0.006C)(0.003C)}{(1.5m)^2}=-k(8*10^{-6}\frac{C^2}{m^2})$

It doesn’t matter if the charges of the two particles are different; both particles experience the same force because the charges of both particles are accounted for in the electrostatic force equation (Coulomb's law). This conclusion can also be made by considering Newton's third law: the force of the first particle on the second will be equal and opposite the force of the second particle on the first.

Since the forces are equal, their ratio will be $\small 1:1$ .

Write, in vector notation, the force exerted on a positive charge of by a negative charge of , if the two charges sitting on the -axis, with the positive charge sitting to the right of the negative charge?

$\vec{F_e}=(-1.80\times10^6 N)\hat{i}+(0N)\hat{j}$

$\vec{F_e}=(-3.6\times10^6 N)\hat{i}+(0N)\hat{j}$

$\vec{F_e}=(0 N)\hat{i}+(-1.80\times10^6 N)\hat{j}$

$\vec{F_e}=(1.80\times10^6 N)\hat{i}+(0N)\hat{j}$

Explanation

Coulomb's law in vector notation is given as:

$F_{e}=\frac{kq_1q_2}{r^2}\hat{r}$ , where is Coulomb's constant, and are the two charges, is the distance between the charges squared, and $\hat{r}$ is the unit vector going from one charge to another.

To write this in vector notation, we have to know the unit vector going from the negative to the positive charge, since we're trying to determine the force on the positive charge. Since they are both sitting on the -axis, with the negative charge to the left of the positive, the unit vector will be going in the direction of positive :

$\hat{r}=<1,0>$

We know that $k=8.99\times10^9 Nm^2C^{-2}$

We know that , , and . Putting this together:

$\vec{F_e}=\frac{8.99\times10^9Nm^2C^{-2} \cdot1C\cdot-2C}{(100:m)^2}<1,0>$

$\vec{F_e}=-1.80*10^6N*<1,0>= <-1.80*10^6N,0N>$

We can rewrite this as:

$\vec{F_e}=(-1.80\times10^6N)\hat{i}+(0N)\hat{j}$

If we have 2 charges, and , that are apart, what is the magnitude of the force exerted on by if we know that has a charge of $10\mu C$ and has a charge of $-20\mu C$ ?

Explanation

Use Coulomb's Law

$F=\frac{kq_1q_2}{r^2}$

Plug in known values and solve.

$\frac{(9\cdot10^{9})(10\cdot10^{-6})(-20\cdot10^{-6})}{0.5^{2}}$

A negative value for electric force indicates an attractive force. This makes sense since our two charges have opposite signs. Since we're asked for magnitude, all answer choices are positive.

If the distance between two charged particles is doubled, the strength of the electric force between them will __________.

be quartered

be halved

quadruple

double

remain unchanged