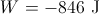AP Physics 1 - Conservation of Energy

Rollercoaster

The height at the top of the hill is

If the velocity of the train at the top of the loop is $28\frac{m}{s }$ , how high is the highest point of the loop?

Explanation

Due to conservation of energy, all energy is conserved throughout this problem. When the train is at the top of the hill, all energy is stored in the form of gravitational potential energy, represented by the equation:

$PE_{_{grav}}=mgh$

Once the train starts rolling down the hill some of that energy gets transferred to kinetic energy, which is represented by the equation:

$KE=\frac{1}{2}mv^{2}$

Because you are given the velocity at the top of the loop it is possible to find the height of the loop by connecting the two equations as follows:

$mgh_{0}=\frac{1}{2}mv^{2}+mgh_{f}$

Where $h_{0}$ is the height at the top of the hill, and $h_{f}$ is the height at any given point in the system. By plugging in the given values and cancelling out the for mass on both sides of the equation, it is possible to find the height at the top of the loop as follows:

$9.81*60=\frac{1}{2}(28^{2})+9.81h_{f}$

$h_{f}\approx20m$

Terry believes he can throw a ball vertically and hit a target above himself. If the ball weighs , how fast must it be traveling when it leaves his hand to just reach the target? Neglect air resistance.

$g=9.81\frac{m}{s^2}$

$31.32\frac{m}{s}$

$15.66\frac{m}{s}$

$22.15\frac{m}{s}$

$981\frac{m}{s}$

$245.25\frac{m}{s}$

Explanation

This problem deals with both potential energy and kinetic energy.

Potential energy is expressed as:

Kinetic energy is expressed as:

$KE=\frac{1}{2}mv^2$

Energy must be conserved, so set up the following equation:

The initial height can be treated as zero, as can the final velocity. Plug in these zero values into the above equation.

Solve for , the initial velocity the ball needs in order to reach a maximum height of .

$v_1=\sqrt{2gh_2}$

$v_1=\sqrt{2\left(9.81\frac{m}{s^2}\right)(50m)}$

$v_1=31.32\frac{m}{s}$

A ball starts rolling up a incline at speed of $17\frac{m}{s}$ . Using conservation of energy, find out how much work gravity does on the ball when it travels from the bottom to the maximum height.

38_deg._incline

$W=-389\ \text{J}$

$W=-846\ \text{J}$

$W=-239\ \text{J}$

$W=-73\ \text{J}$

$W=-736\ \text{J}$

Explanation

The energies involved in this problem are kinetic and potential energy. Conservation of energy shows that the initial energies will be equal to the final energies.

$mgh_i+\frac{1}{2}mv_i^2=mgh_f+\frac{1}{2}mv_f^2$

Choosing the bottom of the incline to be the zero height, the ball starts out with kinetic energy and zero potential energy. When the ball reaches maximum height, its velocity is zero (zero kinetic energy). This simplifies our energy equation.

$0+\frac{1}{2}mv_i^2=mgh_f+0$

Isolate the height variable and use the given values to solve for the maximum height.

$h_f=\frac{v_i^2}{2g}$

$h_f=\frac{(17\frac{m}{s})^2}{2(9.8\frac{m}{s^2})}$

$h_f=14.7\ \text{m}$

This is the vertical height. The work done by gravity is calculated as the product for force and distance.

$W=F_{gravity}h_f=-mgh_f$

The minus sign indicates that the force of gravity acts downward (negative direction).

$W=-(2.7kg)(9.8\frac{m}{s^2})(14.7m)$

$W=-389\ \text{J}$

At a large shipyard in the Atlantic ocean, cranes lift large cargo boxes off of incoming ships. Some of these cargo boxes have a staggering mass near that of . These cranes will then lift these boxes to a height of off the ground. If the cable attached to the cargo boxes were to break when the box was at half it's expected height, at what final velocity will the cargo box be traveling right before it contacts the ground below?

$34\frac{m}{s}$

$52\frac{m}{s}$

$40\frac{m}{s}$

$46\frac{m}{s}$

Explanation

For this question you may use one of two main methods. For this example, the conservation of energy method is shown.

$E_{i}=E_{f}$

Initially, all the energy is stored as gravitational potential energy. At the end of the fall all of the energy will be transformed to kinetic energy.

$mgh=\frac{1}{2}m(v^{2})$

Plug in and solve for the final velocity.

$5000Kg(9.8\frac{m}{s^{2}})(60m)=\frac{1}{2}(5000Kg)v^{2}$

$2,940,000j=2500Kg(v^{2})$

$v=34.4\frac{m}{s}$

The large cargo box will be traveling at $34\frac{m}{s}$ right before it contacts the ground below.

Consider the following system:

Spinning rod with masses at end

Two spherical masses, A and B, are attached to the end of a rigid rod with length l. The rod is attached to a fixed point, p, which is at the midpoint between the masses and is at a height, h, above the ground. The rod spins around the fixed point in a vertical circle that is traced in grey. $\angle c$ is the angle at which the rod makes with the horizontal at any given time ( $c=0^{\circ}$ in the figure).

The rod is spinning and mass A has an instantaneous velocity of $5\frac{m}{s}$ as it passes through the horizontal. What is the velocity of mass A as it passes through its highest point?

$g = 10\frac{m}{s^2}$

Neglect air resistance and internal friction forces.

$5\frac{m}{s}$

$12\frac{m}{s}$

$2\frac{m}{s}$

$1\frac{m}{s}$

$9\frac{m}{s}$

Explanation

This could be a lengthy and complex problem. However, both masses are the same. This simplifies the problem immensely since the total potential energy between the two masses never changes (they both change height at the same rate but in different directions, thus are always the same vertical distance away from point p). Therefore, kinetic energy is never going to change either and the velocity remains constant.

A man throws a pizza in the air. If he released it at a height of , determine the velocity when he released it.

$3.83\frac{m}{s}$

None of these

$4.11\frac{m}{s}$

$5.62\frac{m}{s}$

$6.11\frac{m}{s}$

Explanation

At the maximum height, velocity is zero.

Solving for

$v_i=\sqrt{g(h_f-h_i)}$

Plugging in values

$v_i=\sqrt{9.8(3-1.5)}$

$v_i=3.83\frac{m}{s}$

A block is released from rest on a frictionless ramp inclined at an angle of $40^{\circ}$ with respect to the horizontal. Using conservation of energy methods, calculate the final velocity of the block if it slides a distance of down the incline.

$13.75 \frac{m}{s}$

$15.0 \frac{m}{s}$

$17.16 \frac{m}{s}$

$9.73 \frac{m}{s}$

$6.88 \frac{m}{s}$

Explanation

To solve this problem, we must look at the total energy of the system at two different times: at the beginning before the motion starts, and at the end of the incline. From there, we can use the conservation of energy to solve for the speed of the object at the bottom of the incline.

$E_{initial}=E_{final}\Rightarrow mgh = \frac{1}{2}mv^2\Rightarrow v=\sqrt{2g\Delta x \sin \theta}$

$v=\sqrt{2(9.81\frac{m}{s^2})15m\sin(40^{\circ})}=13.75 \frac{m}{s}$

Conservation of energy is true for what case?

When there are no non-conservative forces $\vec{F}_{nc}$ acting

Conservation of energy is always true

If there are no forces $\vec{F}$ acting

When the direction of the force is perpendicular to the motion

Explanation

By definition, the total mechanical energy of a system is always be conserved except in the presence of non-conservative forces, namely friction and air resistance.

A pebble is dropped from a height of . What is its speed before it hits the ground? Disregard the effects of air resistance.