Fundamentals of Force and Newton's Laws - AP Physics 1

Card 0 of 476

Question

A block of mass moves down an inclined plane of angle $\theta$ with a constant velocity as shown below. The coefficient of friction between the block and the inclined plane is given by $\mu_k$ .

What is the value of $\mu_k$ in terms of , , , and $\theta$ ?

Answer

The free body diagram of the block is given above. This block has three forces acting on it. First, it's weight under the influence of gravity, which is given as . Second, the normal force of the plane, which is given as . Third, the friction force, which acts opposite to its direction of motion and is given as $\mu_kF_N$ . We choose a coordinate system so that our x-axis aligns with the motion of the block down the plane, and the y-axis aligns with the direction of the normal force. Thus the friction force points in the negative direction of the x-axis, and the normal force is aligned with the positive direction of the y-axis. However, the weight is not along either of these axes, so we resolve the force into its components, $mg\cos(\theta)$ along the negative y-axis, and $mg\sin(\theta)$ along the positive x-axis.

Now we can use Newton's 2nd law to relate the given forces above. Newton's 2nd law gives us two equations:

$\sum F_x=ma_x$ and $\sum F_y=ma_y$

Because the block is constrained to move along the surface of the inclined plane, there should be no acceleration in the y direction, and so . Also, because the block moves at constant velocity down the plane, Newton's 1st law assures us that there is no acceleration in the x direction as well, therefore . Plugging these accelerations in, we find that $\sum F_x=0$ and $\sum F_y=0$

Summing all the forces in the x-direction gives us

$\sum F_x=mg\sin(\theta)-\mu_kF_N$

Summing all the forces in the y-direction gives us

$\sum F_y=F_N-mg\cos(\theta)$

Plugging these values into the force equations above gives us the following equations:

$mg\sin(\theta)-\mu_kF_N=0$

$F_N-mg\cos(\theta)=0$

Solving for in the second equation gives us $F_N=mg\cos(\theta)$ . Thus the normal force is equal to the cosine component of the weight. Substituting $mg\cos(\theta)$ in for in the first equation will give us the following:

$mg\sin(\theta)-\mu_kmg\cos(\theta)=0$

Now we solve the equation for $\mu_k$ . Adding $\mu_kmg\cos(\theta)$ to each side gives us:

$mg\sin(\theta)=\mu_kmg\cos(\theta)$

Now we divide each side by $mg\cos(\theta)$ to obtain:

$\mu_k=\frac{mg\sin(\theta)}{mg\cos(\theta)}=\tan(\theta)$

The final result is obtained by canceling the factor and using the triginometric identity:

$\frac{\sin(\theta)}{\cos(\theta)}=\tan(\theta)$

Therefore we arrive at the conclusion that $\mu_k=\tan(\theta)$

Compare your answer with the correct one above

Question

All of the following statements are true. Which of them is NOT explained by Newton's first law of motion?

Answer

Newton's first law of motion refers to objects with no external forces acting on them. Objects with no external forces will maintain the same velocity, meaning that

(1) if they are not moving, they will continue not moving

(2) if they are moving, they will keep moving with the same speed and direction

The answer "Dropping a box causes it to accelerate downwards" refers to a box with a force acting upon it—the force of gravity. Also, the box is accelerating, unlike objects referred to by Newton's first law of motion, which have constant velocities.

Compare your answer with the correct one above

Question

You are traveling on an airplane at constant speed of 650mph. Your friend is traveling in his car at a constant speed of 60mph. Who experiences a larger acceleration?

Answer

Since both you and your friend are traveling at a constant speed, the acceleration of you and your friend is zero. Thus, neither you nor your friend experiences any acceleration. This can be shown mathematically using the equation for acceleration:

$a=\frac{\Delta v}{\Delta t}$

Since there is no change in velocity over time acceleration is zero. Also note that when acceleration is zero, so is the net force.

Compare your answer with the correct one above

Question

You are sitting in a car, at rest, when another car rear ends your vehicle. Why do you and the passengers experience a whiplash, in terms of Newton's laws of motion?

Answer

Because an object at rest tends to stay at rest, when your car is hit your body/neck will 'want' to stay where it was. This will cause your body and neck to 'whip' as it will take time for it to speed up from being hit.

Compare your answer with the correct one above

Question

A van with helium-filled party balloons is driving around when it approaches a red light. When the van is slowing down to come to a complete stop, in which direction do the balloons go?

Answer

According to Newton's First Law of Motion, something in motion will stay in motion unless acted on by another force. As the van slows down, we expect free object in the van to continue moving forward within the van. However, helium is lighter than air so the air in the van will continue to move forward, leaving the light balloons in the back of the van.

Compare your answer with the correct one above

Question

During time period , a rocket ship deep in space of mass travels from to . During time period , the rocket fires. During time period , the rocket travels from to .

Time periods , , and all took

Determine the average force during time period .

Answer

Finding initial momentum:

$\overrightarrow{P}=m\overrightarrow{v}$

$\overrightarrow{v}=\frac{<x_f-x_i,y_f-y_i>}{t}$

Combining equations:

$\overrightarrow{P}=m\frac{<x_f-x_i,y_f-y_i>}{t}$

Plugging in values:

$\overrightarrow{P}=2.5510^5\frac{<5000-0,5000-10000>}{10}$

$\overrightarrow{P_i}=<1.27510^8,-1.27510^8>\frac{kgm}{s}$

$\overrightarrow{P}=m\overrightarrow{v}$

$\overrightarrow{v}=\frac{<x_f-x_i,y_f-y_i>}{t}$

Combining equations:

$\overrightarrow{P}=m\frac{<x_f-x_i,y_f-y_i>}{t}$

Converting to and plugging in values:

$\overrightarrow{P}=2.5510^5\frac{<-30000+15000,-5000-0>}{10}$

$\overrightarrow{P}_f=<-3.82510^8,-1.27510^8>\frac{kgm}{s}$

Using

$Impulse=\Delta\overrightarrow{P}=\overrightarrow{P_f}-\overrightarrow{P_i}$ Plugging in values:

$\overrightarrow{\Delta P} =<-3.82510^8,-1.27510^8>-<1.27510^8,-1.27510^8>$

$\Delta\overrightarrow{P}=<5.110^8,0>\frac{kgm}{s}$

Using:

$\Delta \overrightarrow{P}=\overrightarrow{F}\Delta t$

Solving for $\overrightarrow{F}$ and plugging in values

$\overrightarrow{F}=\frac{<5.110^8,0>\frac{kgm}{s}}{10s}$

$\overrightarrow{F}=5.110^7\ \frac{\textup{m}}{\textup{s}}$

Compare your answer with the correct one above

Question

Consider the following system:

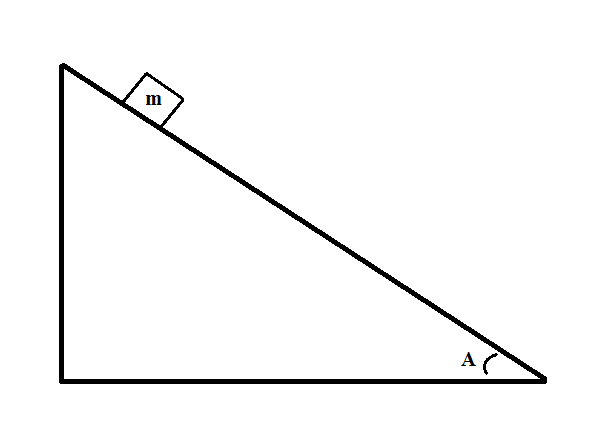
If the mass accelerates down the plane at a rate of $7\frac{m}{s^2}$ and the angle $A = 60^{\circ}$ , what is the coefficient of kinetic friction between the mass and slope?

$g = 10\frac{m}{s^2}$

Answer

Before we start using equations, we need to determine what forces are acting on the block in this system. The only relevant forces in this situation are gravity and friction. We are given the acceleration of the block, giving us the tools to find the net force.

Using Newton's second law, we can write:

$F_{net}=ma$

The force of friction is subtracted because it is in the opposite direction of the movement of the block. Substituting in expressions for each variable, we get:

$mgsin(\theta) - \mu_k mgcos(\theta) = ma$

Canceling out mass and rearranging for the coefficient of kinetic friction, we get:

$\mu_k = \frac{gsin(\theta)-a}{gcos(\theta)}$

We have values for each variable, allowing us to solve:

$\mu_k = \frac{(10\frac{m}{s^2})sin(60^{\circ})-7\frac{m}{s^2}}{(10\frac{m}{s^2})cos(60^{\circ})}$

$\mu_k = 0.33$

Compare your answer with the correct one above

Question

Consider the following system:

This system is set on a different planet, which has a gravitational constant different from that on Earth. If the angle measures $40^{\circ}$ , the coefficient of kinetic friction is , and the block is accelerating at a rate of $12\frac{m}{s^2}$ , what is the gravitational acceleration on this planet?

Answer

There are two relevant forces acting on the block in this scenario: gravity and friction. We can use Newton's second law to solve this problem:

$F_{net} = ma$

Substituting in expressions for each force, we get:

$mgsin(\theta) - \mu_kmgcos(\theta) = ma$

Eliminating mass and rearranging for , we get:

$g = \frac{a}{sin(\theta)-\mu_kcos(\theta)}$

At this point, we can plug in values for each variable and solve:

$g = \frac{12\frac{m}{s^2}}{sin(40^{\circ})-(0.35)cos(40^{\circ})}$

$g = 18.4\frac{m}{s^2}$

Compare your answer with the correct one above

Question

In the diagram, a massless string connects two blocks of mass 30 kg and 50 kg that are on a flat, frictionaless surface. A force pulls on the 50 kg block, as shown. If the force pulling on the 50 kg block is 100 N, what is the tension in the string connecting the two blocks?

Answer

Start by drawing in the forces acting on each block. You could also draw in the force of gravity and the normal force for each block, but they have been omitted from the image because they cancel each other out for each block and because there is no friction in this problem.

We are given in the question that the force is 100 N. Since the blocks are connected by a string, they will therefore accelerate at the same rate, and we can treat them as a system that moves as if it were one object of total mass 80 kg (30 kg plus 50 kg). Use Newton's second law:

$F_{net}=ma$

In this problem, the two tension forces form an action/reaction pair and therefore are equal in magnitude but opposite in direction (Newton's third law). So:

$100:N-T+T=80:kg\cdot a$

We can solve for acceleration, since the tensions cancel out.

$a=\frac{100:N}{80:kg}=1.25:\frac{m}{s^2}$

Now that we have acceleration, we need to write a new equation in which the tension force does not cancel out so that we can solve for the tension .

Do this by using Newton's second law again, except for only one of the blocks:

$F_{net}=ma$

Lets consider the 30 kg block. The only force acting on the 30 kg block is the tension , and the acceleration is what we found above.

$T=30:kg\cdot 1.25:\frac{m}{s^2}=38:N$

Compare your answer with the correct one above

Question

A ball with mass is on a ramp as illustrated below:

Find the magnitude of the ball's normal force.

Answer

The normal force is perpendicular to the plane:

First, we need to find $\theta$ .

We can solve for $\theta$ using the trigonometric equation that applies in this instance. We know the length of the side opposite of $\theta$ (5 m) and the length of the side adjacent to $\theta$ (10 m), so we can use the following equation to solve for $\theta$ :

$tan\theta=\frac{l_{opposite}}{l_{adjacent}}$

Rearranging to solve this equation for $\theta$ , you get

$\theta=arctan(\frac{l_{adjacent}}{l_{opposite}})$

Substituting in the side lengths of the given triangle, we can solve for $\theta$ .

$\theta = \arctan\left(\frac{5}{10} \right)=26.6^\circ$

Note that the normal force is one of the legs of another right triangle. The other leg is the parallel force, and the hypotenuse is the force of gravity.

Using trigonometry, we know that

$F_n=F_g \cos{\theta}$

because $cos\theta=\frac{l_{adjacent}}{l_{hypotenuse}}$ , or, in terms of this problem, $l_{adjacent}=cos\theta\cdot l_{hypotenuse}$ .

Substituting in the known values into this equation, we can solve for the normal force:

$F_n=(9.81\frac{m}{s^2}\cdot m) \cos{26.6^\circ}=8.77\frac{m^2}{s^2} \cdot m$

Compare your answer with the correct one above

Question

A man shoots a rifle and the force of the shot results in recoil. The magnitude of the force on the rifle the magnitude of force on the bullet, and the magnitude of acceleration of the rile that of the bullet.

Answer

Consistent with Newton's third law, which states that every force has an equal and opposite reaction, the force on the rifle is equal to the force on the bulet. However, the rifle has a larger mass, so the magnitude of its acceleration is less than that of the bullet.

Compare your answer with the correct one above

Question

$\theta=30^{\textup o}$

What is the acceleration of the block above if its mass is and the coefficient of kinetic friction is ?

$g = 10\frac{m}{s^s}$

Answer

$F=mg=5kg\left(10\frac{m}{s^2} \right)=50N$

The component of perpendicular to the slope is $mg\cdot cos\theta$ , where $\theta$ is the angle between the ground and the incline.

$50N\cdot cos(30^{\text o}) = 43.3N = -F_N$ where is the normal force.

The force of friction, which is in the direction opposing motion is:

$F_{fr}=\mu_k F_{N}=0.2\cdot43.3N=8.66N$

$\mu_k$ is the coefficient of kinetic friction.

The component of parallel to the slope is:

$mg\cdot sin\theta = 50N\sin 30^{\textup o} = 25N$

The net force on the block is:

$F_{net}=F_{perpendicular}-F_N+F_{parallel}-F_{fr}$

$F_{net}=43.3N-43.3N+25N-8.66N=16.34N$

$F_{net}=ma$

$16.34N=5kg\cdot a$

$a=3.37\frac{m}{s^2}$

Compare your answer with the correct one above

Question

$g=9.81\frac{m}{s^2}$

A mass is suspended by two cables. What is the magnitude of the tension in the left cable?

Answer

Begin by diagraming the forces acting on the mass in the problem:

The mass itself creates a force due to gravity in the downward direction:

$\overrightarrow{W}=-mg\widehat{j}=-35kg(9.81\frac{m}{s^2})\widehat{j}$

$\overrightarrow{W}=-343.4N\widehat{j}$

For the mass to remain stationary, the forces must be in equilibrium. Therefore the sum of forces in the x and y directions each must be zero:

$F_y=T_{1y}+T_{2y}-W=0$

$F_x=T_{2x}-T_{1x}=0$

The x and y tensions can be written in terms of the magnitude of the tension in each cable. Begin with the x direction:

$T_2cos(30^{\circ})-T_1cos(30^{\circ})=0$

Because the angle is the same for each, the tension in each angle must be equivalent. Use this property when performing the force balance in the y direction:

$T_1sin(30^{\circ})+T_2sin(30^{\circ})-W=0$

$2T_1sin(30^{\circ})=W$

Compare your answer with the correct one above

Question

$g=9.81\frac{m}{s^2}$

A mass is supported by two cables. What is the magnitude of tension in the right cable?

Answer

Begin by drawing a force diagram of forces acting on the mass:

The mass itself creates a force due to gravity in the downward direction.

For the mass to remain stationary, the forces must be in equilibrium. Therefore the sum of forces in the x and y directions each must be zero:

$F_y=T_{1y}+T_{2y}-W=0$

$F_x=T_{2x}-T_{1x}=0$

The x and y tensions can be written in terms of the magnitude of the tension in each cable. Begin with the x direction:

$T_2cos(60^{\circ})-T_1cos(60^{\circ})=0$

Because the angle is the same for each, the tension in each angle must be equivalent. Use this property when performing the force balance in the y direction:

$T_1sin(60^{\circ})+T_2sin(60^{\circ})-W=0$

$2T_2sin(60^{\circ})=W$

$2T_2sin(60^{\circ})=9.81\frac{m}{s^2}(50kg)$

$T_2=\frac{1}{2sin(60^{\circ})}9.81\frac{m}{s^2}(50kg)$

Compare your answer with the correct one above

Question

$g=9.81\frac{m}{s^2}$

A 50kg mass is supported by two cables. Find the magnitude of tension in the left cable.

Answer

Begin by diagraming the forces acting on the mass:

The mass itself creates a force due to gravity in the downward direction.

For the mass to remain stationary, the forces must be in equilibrium. Therefore the sum of forces in the x and y directions each must be zero:

$F_y=T_{1y}+T_{2y}-W=0$

$F_x=T_{2x}-T_{1x}=0$

The x and y tensions can be written in terms of the magnitude of the tension in each cable. Begin with the x direction:

$T_2cos(30^{\circ})-T_1cos(60^{\circ})=0$

$T_2=\frac{1}{2cos(30^{\circ})}T_1$

Because the angle is the same for each, the tension in each angle must be equivalent. Use this property when performing the force balance in the y direction:

$T_1sin(60^{\circ})+T_2sin(30^{\circ})-W=0$

$T_1sin(60^{\circ})+(\frac{1}{2cos(30^{\circ})}T_1)sin(30^{\circ})-W=0$

$T_1(sin(60^{\circ})+\frac{tan(30^{\circ})}{2})=W$

$T_1=\frac{1}{sin(60^{\circ})+\frac{tan(30^{\circ})}{2}}W$

$T_1=\frac{1}{sin(60^{\circ})+\frac{tan(30^{\circ})}{2}}(50kg)(9.81\frac{m}{s^2})$

Compare your answer with the correct one above

Question

Two forces are exerted on the center of an object. What angle between the two forces would provide the largest resultant force?

Answer

Imagine two men of equal strength pulling on ropes that are connected to a crate. In order to obtain the largest resulting force the two men should pull in the same direction at $0^{\circ}$ . Pulling on opposite ends at $180^{\circ}$ would result in zero resultant force and anything besides $0^{\circ}$ would cause the force to act in an unneeded direction.

Compare your answer with the correct one above

Question

Which of the following is true when an object has reached terminal velocity?

Answer

During terminal velocity:

Thus, by Newton's second law:

$F_{net}=ma=0$

$F_{net}=F_g+F_{air}=0$

Compare your answer with the correct one above

Question

Suppose that an object with a mass of is free-falling in the air. If we neglect the influence of friction, what upward force must be applied to the falling object if we want it to reach a constant velocity?

Answer

In this question, we're told that an object of a given mass is free-falling in the air with no air resistance. We're asked to determine the amount of upward force necessary to cause this object's velocity to become constant.

In order for an object's velocity to be maintained at a constant value, that object must not be accelerating. Therefore, we'll need to determine what force will allow this object to have a net acceleration of zero.

Looking at the falling object's motion in the downward direction, we know that it is falling due to the influence of gravity. Since we know its mass, we can calculate this downward force:

$F_{down}=ma_{down}$

$F_{down}=(15:kg)(9.8: \frac{m}{s^{2}})=147:N$

We've stated that in order to have a constant velocity, we need to have a net acceleration of zero. And since we know that the object is accelerating by $9.8: \frac{m}{s^{2}}$ in the downward direction, we will need it to accelerate upward by $9.8: \frac{m}{s^{2}}$ to cancel it to zero.

$F_{up}=ma_{up}$

$F_{up}=(15:kg)(9.8: \frac{m}{s^{2}})=147:N$

To conclude, we'll have to match the downward force by presenting an equal upward force in order to cancel out the object's acceleration and bring its velocity to a constant value.

Compare your answer with the correct one above

Question

If people lift a car, how much force would each person have to apply to hold the car steady off the ground?

Answer

Using definition of force and superposition of Forces

Each person is apply the same amount of force against gravity. The car is holding still so it has no acceleration.

Solving for and plugging in values, remembering that gravity points downwards and thus is negative.

$F_P=\frac{-2000*-9.8}{10}$

Compare your answer with the correct one above

Question

If three locomotives are pulling a train, how much force does each locomotive need to apply to accelerate the train at $1\frac{cm}{s^2}$ from rest?

Answer

Using

Converting $\frac{cm}{s^2}$ to $\frac{m}{s^2}$ and plugging in values.

Compare your answer with the correct one above

Tap the card to reveal the answer