Fundamental Theorem of Calculus and Techniques of Antidifferentiation - AP Calculus BC
Card 1 of 170
Evaluate:

Evaluate:
Tap to reveal answer
First, we will find the indefinite integral  using integration by parts.
using integration by parts.
We will let  and
and  .
.
Then  and
and  .
.






To find  , we use another integration by parts:
, we use another integration by parts:
 , which means that
, which means that  , and
, and
 , which means that, again,
, which means that, again,  .
.











Since
 , or,
, or,

for all real  , and
, and
 ,
,
by the Squeeze Theorem,
 .
.







First, we will find the indefinite integral 
We will let 

Then 

To find 




Since

for all real 

by the Squeeze Theorem,



← Didn't Know|Knew It →
Evaluate:

Evaluate:
Tap to reveal answer
First, we will find the indefinite integral,  .
.
We will let  and
and  .
.
Then,
 and
and  .
.

and







Now, this expression evaluated at  is equal to
is equal to
 .
.
At  it is undefined, because
it is undefined, because  does not exist.
does not exist.
We can use L'Hospital's rule to find its limit as  , as follows:
, as follows:

 and
and  , so by L'Hospital's rule,
, so by L'Hospital's rule,

Therefore,


![=\lim _{b\rightarrow 0}\left [ \left.\begin{matrix} $\frac{ x ^{2}$$\ln{x}$}{2} - $$\frac{x^{2}$$}{4} \ \ \end{matrix}\right| \begin{matrix} 1\ \ b \end{matrix} \right]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/180705/gif.latex)


First, we will find the indefinite integral, 
We will let 

Then,


and
Now, this expression evaluated at 

At 

We can use L'Hospital's rule to find its limit as 


Therefore,
← Didn't Know|Knew It →
Evaluate:

Evaluate:
Tap to reveal answer
Rewrite the integral as
 .
.
Substitute  . Then
. Then
 and
and  . The lower bound of integration stays
. The lower bound of integration stays  , and the upper bound becomes
, and the upper bound becomes  , so
, so


Since  , the above is equal to
, the above is equal to
 .
.
Rewrite the integral as

Substitute 




Since 

← Didn't Know|Knew It →
Evaluate  .
.
Evaluate 
Tap to reveal answer
By the Formula Rule, we know that  . We therefore know that
. We therefore know that  .
.
Continuing the calculation:



By the Power Rule for Integrals,  for all
for all  with an arbitrary constant of integration
with an arbitrary constant of integration  . Therefore:
. Therefore:



 .
.
So, 


 .
.


By the Formula Rule, we know that 

Continuing the calculation:
By the Power Rule for Integrals, 



So,

← Didn't Know|Knew It →
Tap to reveal answer
In order to evaluate this integral, we will need to use partial fraction decomposition.

Multiply both sides of the equation by the common denominator, which is 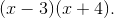


This means that  must equal 1, and
must equal 1, and 



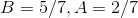
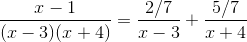
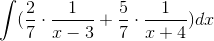



The answer is  .
.
In order to evaluate this integral, we will need to use partial fraction decomposition.
Multiply both sides of the equation by the common denominator, which is
This means that 
The answer is 
← Didn't Know|Knew It →
Integrate:

Integrate:
Tap to reveal answer
To integrate, we must first make the following substitution:

Rewriting the integral in terms of u and integrating, we get
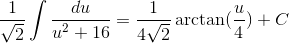
The following rule was used to integrate:

Finally, we replace u with our original x term:

To integrate, we must first make the following substitution:
Rewriting the integral in terms of u and integrating, we get
The following rule was used to integrate:
Finally, we replace u with our original x term:
← Didn't Know|Knew It →
Evaluate  :
:

Evaluate 
Tap to reveal answer
By the Fundamental Theorem of Calculus, we have that  . Thus,
. Thus,  .
.
By the Fundamental Theorem of Calculus, we have that 

← Didn't Know|Knew It →
Find the result:

Find the result:
Tap to reveal answer
Set  . Then
. Then  , and by the chain rule,
, and by the chain rule,



By the fundamental theorem of Calculus, the above can be rewritten as



Set 

By the fundamental theorem of Calculus, the above can be rewritten as
← Didn't Know|Knew It →
Suppose we have the function

What is the derivative,  ?
?
Suppose we have the function
What is the derivative, 
Tap to reveal answer
We can view the function  as a function of
as a function of  , as so
, as so

where  .
.
We can find the derivative of  using the chain rule:
using the chain rule:

where  can be found using the fundamental theorem of calculus:
can be found using the fundamental theorem of calculus:

So we get
![\small \small \small \small g'(x)=-\sin x\cdot F'(\cos x)=-\sin x\cdot[1+\sin(\cos x)]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/375920/gif.latex)
We can view the function 

where 
We can find the derivative of 
where 
So we get
← Didn't Know|Knew It →
Evaluate  when
when  .
.
Evaluate 

Tap to reveal answer
Via the Fundamental Theorem of Calculus, we know that, given a function ,
,  .
.
Therefore  .
.
Via the Fundamental Theorem of Calculus, we know that, given a function

Therefore 
← Didn't Know|Knew It →
Evaluate  when
when  .
.
Evaluate 

Tap to reveal answer
Via the Fundamental Theorem of Calculus, we know that, given a function  ,
,  . Therefore,
. Therefore,  .
.
Via the Fundamental Theorem of Calculus, we know that, given a function 


← Didn't Know|Knew It →
Given
 , what is
, what is  ?
?
Given


Tap to reveal answer
By the Fundamental Theorem of Calculus, for all functions  that are continuously defined on the interval
that are continuously defined on the interval ![[a,b]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/387903/gif.latex) with
with  in
in ![[a,b]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/387905/gif.latex) and for all functions
and for all functions  defined by by
defined by by  , we know that
, we know that  .
.
Thus, for
 ,
,
 .
.
Therefore,

By the Fundamental Theorem of Calculus, for all functions 
![[a,b]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/387903/gif.latex)

![[a,b]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/387905/gif.latex)



Thus, for


Therefore,
← Didn't Know|Knew It →
Given
 , what is
, what is  ?
?
Given


Tap to reveal answer
By the Fundamental Theorem of Calculus, for all functions  that are continuously defined on the interval
that are continuously defined on the interval ![[a,b]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/387910/gif.latex) with
with  in
in ![[a,b]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/387912/gif.latex) and for all functions
and for all functions  defined by by
defined by by  , we know that
, we know that  .
.
Given
 , then
, then
 .
.
Therefore,
 .
.
By the Fundamental Theorem of Calculus, for all functions 
![[a,b]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/387910/gif.latex)

![[a,b]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/387912/gif.latex)



Given


Therefore,

← Didn't Know|Knew It →
Evaluate 
Evaluate
Tap to reveal answer

Use the fundamental theorem of calculus to evaluate:
![$\frac{1}{3}$ $(6-3)^3$ - [ $$\frac{1}{3}$(0-3)^3$] = $\frac{1}{3}$ $(3)^3$ - $\frac{1}{3}$ $(-3)^3$](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/854677/gif.latex)

Use the fundamental theorem of calculus to evaluate:
← Didn't Know|Knew It →
Tap to reveal answer

Use the Fundamental Theorem of Calculus and evaluate the integral at both endpoints:


Use the Fundamental Theorem of Calculus and evaluate the integral at both endpoints:
← Didn't Know|Knew It →
Tap to reveal answer

Use the Fundamental Theorem of Calculus and evaluate the integral at both endpoints:
![$\frac{4}{3}$ $(3)^3$ - $\frac{1}{2}$ $(3)^2$ - [ $\frac{4}{3}$ $(-1)^3$ - $\frac{1}{2}$ $(-1)^2$]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/854844/gif.latex)
![= 36 - 4.5 - [ -$\frac{4}{3}$ - $\frac{1}{2}$ ] = 36 - 4.5 + 1. $\overline{3}$ + .5 = 33. $\overline{3}$](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/854845/gif.latex)
Use the Fundamental Theorem of Calculus and evaluate the integral at both endpoints:
← Didn't Know|Knew It →
Evaluate the following integral

Evaluate the following integral
Tap to reveal answer
Evaluate the following integral

Let's begin by recalling our "reverse power rule" AKA, the antiderivative form of our power rule.

In other words, all we need to do for each term is increase the exponent by 1 and then divide by that number.

Let's clean it up a little to get:

Now, to evaluate our integral, we need to plug in 5 and 0 for x and find the difference between the values. In other words, if our integrated function is F(x), we need to find F(5)-F(0).
Let's start with F(5)

Next, let's look at F(0). If you look at our function carefully, you will notice that F(0) will cancel out all of our terms except for +c. So, we have the following:


Finding the difference cancels out the c's and leaves us with 185.

Evaluate the following integral
Let's begin by recalling our "reverse power rule" AKA, the antiderivative form of our power rule.
In other words, all we need to do for each term is increase the exponent by 1 and then divide by that number.
Let's clean it up a little to get:
Now, to evaluate our integral, we need to plug in 5 and 0 for x and find the difference between the values. In other words, if our integrated function is F(x), we need to find F(5)-F(0).
Let's start with F(5)
Next, let's look at F(0). If you look at our function carefully, you will notice that F(0) will cancel out all of our terms except for +c. So, we have the following:
Finding the difference cancels out the c's and leaves us with 185.
← Didn't Know|Knew It →
Tap to reveal answer
In order to evaluate this integral, we will need to use partial fraction decomposition.

Multiply both sides of the equation by the common denominator, which is 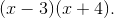


This means that  must equal 1, and
must equal 1, and 



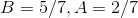
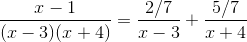
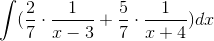



The answer is  .
.
In order to evaluate this integral, we will need to use partial fraction decomposition.
Multiply both sides of the equation by the common denominator, which is
This means that 
The answer is 
← Didn't Know|Knew It →
Integrate:

Integrate:
Tap to reveal answer
To integrate, we must first make the following substitution:

Rewriting the integral in terms of u and integrating, we get
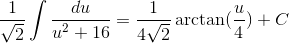
The following rule was used to integrate:

Finally, we replace u with our original x term:

To integrate, we must first make the following substitution:
Rewriting the integral in terms of u and integrating, we get
The following rule was used to integrate:
Finally, we replace u with our original x term:
← Didn't Know|Knew It →
Evaluate:

Evaluate:
Tap to reveal answer
First, we will find the indefinite integral  using integration by parts.
using integration by parts.
We will let  and
and  .
.
Then  and
and  .
.






To find  , we use another integration by parts:
, we use another integration by parts:
 , which means that
, which means that  , and
, and
 , which means that, again,
, which means that, again,  .
.











Since
 , or,
, or,

for all real  , and
, and
 ,
,
by the Squeeze Theorem,
 .
.







First, we will find the indefinite integral 
We will let 

Then 

To find 




Since

for all real 

by the Squeeze Theorem,



← Didn't Know|Knew It →


