Parametric, Polar, and Vector Functions - AP Calculus BC
Card 1 of 390
Find the vector form of  to
to  .
.
Find the vector form of 

Tap to reveal answer
When we are trying to find the vector form we need to remember the formula which states to take the difference between the ending and starting point.
Thus we would get:
Given  and
and 
![\overrightarrow{v}=[d-a, e-b, f-c]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/327010/gif.latex)
In our case we have ending point at  and our starting point at
and our starting point at  .
.
Therefore we would set up the following and simplify.
![\overrightarrow{v}=[6-0,3-1,1-3]=[6,2,-2]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/327013/gif.latex)
When we are trying to find the vector form we need to remember the formula which states to take the difference between the ending and starting point.
Thus we would get:
Given 
In our case we have ending point at 

Therefore we would set up the following and simplify.
← Didn't Know|Knew It →
Tap to reveal answer
In general:
If  ,
,
then 
Derivative rules that will be needed here:
- Taking a derivative on a term, or using the power rule, can be done by doing the following:

- Special rule when differentiating an exponential function:
 , where k is a constant.
, where k is a constant.
In this problem, 



Put it all together to get 

In general:
If 
then
Derivative rules that will be needed here:
- Taking a derivative on a term, or using the power rule, can be done by doing the following:
- Special rule when differentiating an exponential function:
, where k is a constant.
In this problem,
Put it all together to get
← Didn't Know|Knew It →

Calculate 
Calculate
Tap to reveal answer
Calculate the sum of vectors.
In general,



Solution:




Calculate the sum of vectors.
In general,
Solution:
← Didn't Know|Knew It →
Given points  and
and  , what is the vector form of the distance between the points?
, what is the vector form of the distance between the points?
Given points 

Tap to reveal answer
In order to derive the vector form of the distance between two points, we must find the difference between the  ,
,  , and
, and  elements of the points.
elements of the points.
That is, for any point
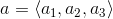 and
and  ,
,
the distance is the vector
 .
.
Subbing in our original points  and
and  , we get:
, we get:


In order to derive the vector form of the distance between two points, we must find the difference between the ,
, and
elements of the points.
That is, for any point
and
,
the distance is the vector
.
Subbing in our original points 

← Didn't Know|Knew It →
Given points  and
and  , what is the vector form of the distance between the points?
, what is the vector form of the distance between the points?
Given points 

Tap to reveal answer
In order to derive the vector form of the distance between two points, we must find the difference between the  ,
,  , and
, and  elements of the points.
elements of the points.
That is, for any point 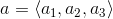 and
and  , the distance is the vector
, the distance is the vector  .
.
Subbing in our original points  and
and  , we get:
, we get:


In order to derive the vector form of the distance between two points, we must find the difference between the ,
, and
elements of the points.
That is, for any point and
, the distance is the vector
.
Subbing in our original points 

← Didn't Know|Knew It →
The graph of the vector function  can also be represented by the graph of which of the following functions in rectangular form?
can also be represented by the graph of which of the following functions in rectangular form?
The graph of the vector function 
Tap to reveal answer
We can find the graph of  in rectangular form by mapping the parametric coordinates to Cartesian coordinates
in rectangular form by mapping the parametric coordinates to Cartesian coordinates 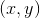 :
:


We can now use this value to solve for  :
:
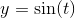

We can find the graph of 
:
We can now use this value to solve for :
← Didn't Know|Knew It →
The graph of the vector function  can also be represented by the graph of which of the following functions in rectangular form?
can also be represented by the graph of which of the following functions in rectangular form?
The graph of the vector function 
Tap to reveal answer
We can find the graph of  in rectangular form by mapping the parametric coordinates to Cartesian coordinates
in rectangular form by mapping the parametric coordinates to Cartesian coordinates 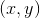 :
:




We can now use this value to solve for  :
:

We can find the graph of 
:
We can now use this value to solve for :
← Didn't Know|Knew It →
What is the derivative of  ?
?
What is the derivative of 
Tap to reveal answer
In order to find the derivative  of a polar equation
of a polar equation  , we must first find the derivative of
, we must first find the derivative of  with respect to
with respect to  as follows:
as follows:

We can then swap the given values of  and
and  into the equation of the derivative of an expression into polar form:
into the equation of the derivative of an expression into polar form:




Using the trigonometric identity  , we can deduce that
, we can deduce that  . Swapping this into the denominator, we get:
. Swapping this into the denominator, we get:



In order to find the derivative 



We can then swap the given values of 

Using the trigonometric identity 

← Didn't Know|Knew It →
What is the polar form of  ?
?
What is the polar form of 
Tap to reveal answer
We can convert from rectangular to polar form by using the following trigonometric identities: 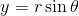 and
and  . Given
. Given  , then:
, then:


Dividing both sides by 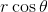 , we get:
, we get:





We can convert from rectangular to polar form by using the following trigonometric identities: and
. Given

Dividing both sides by , we get:
← Didn't Know|Knew It →
Rewrite in polar form:

Rewrite in polar form:
Tap to reveal answer
← Didn't Know|Knew It →
Graph the equation  where
where  .
.
Graph the equation 

Tap to reveal answer
At angle  the graph as a radius of
the graph as a radius of  . As it approaches
. As it approaches  , the radius approaches
, the radius approaches  .
.
As the graph approaches  , the radius approaches
, the radius approaches  .
.
Because this is a negative radius, the curve is drawn in the opposite quadrant between  and
and  .
.
Between  and
and  , the radius approaches
, the radius approaches  from
from  and redraws the curve in the first quadrant.
and redraws the curve in the first quadrant.
Between  and
and  , the graph redraws the curve in the fourth quadrant as the radius approaches
, the graph redraws the curve in the fourth quadrant as the radius approaches  from
from  .
.
At angle 



As the graph approaches 

Because this is a negative radius, the curve is drawn in the opposite quadrant between 

Between 



Between 



← Didn't Know|Knew It →
Draw the graph of  from
from  .
.
Draw the graph of 

Tap to reveal answer
Because this function has a period of  , the x-intercepts of the graph
, the x-intercepts of the graph  happen at a reference angle of
happen at a reference angle of  (angles halfway between the angles of the axes).
(angles halfway between the angles of the axes).
Between  and
and  the radius approaches
the radius approaches  from
from  .
.
Between  and
and  , the radius approaches
, the radius approaches  from
from  and is drawn in the opposite quadrant, the third quadrant because it has a negative radius.
and is drawn in the opposite quadrant, the third quadrant because it has a negative radius.
From  to
to  the radius approaches
the radius approaches  from
from  , and is drawn in the fourth quadrant, the opposite quadrant.
, and is drawn in the fourth quadrant, the opposite quadrant.
Between  and
and  , the radius approaches
, the radius approaches  from
from  .
.
From  and
and  , the radius approaches
, the radius approaches  from
from  .
.
Between  and
and  , the radius approaches
, the radius approaches  from
from  . Because it is a negative radius, it is drawn in the opposite quadrant, the first quadrant.
. Because it is a negative radius, it is drawn in the opposite quadrant, the first quadrant.
Then between  and
and  the radius approaches
the radius approaches  from
from  and is draw in the second quadrant.
and is draw in the second quadrant.
Finally between  and
and  , the radius approaches
, the radius approaches  from
from  .
.
Because this function has a period of 


Between 



Between 



From 



Between 



From 



Between 



Then between 



Finally between 



← Didn't Know|Knew It →
What is the following coordinate in polar form?

Provide the angle in degrees.
What is the following coordinate in polar form?
Provide the angle in degrees.
Tap to reveal answer
To calculate the polar coordinate, use



However, keep track of the angle here. 68 degree is the mathematical equivalent of the expression, but we know the point (-2,-5) is in the 3rd quadrant, so we have to add 180 to it to get 248.
Some calculators might already have provided you with the correct answer.
 .
.
To calculate the polar coordinate, use
However, keep track of the angle here. 68 degree is the mathematical equivalent of the expression, but we know the point (-2,-5) is in the 3rd quadrant, so we have to add 180 to it to get 248.
Some calculators might already have provided you with the correct answer.

← Didn't Know|Knew It →
What is the equation  in polar form?
in polar form?
What is the equation 
Tap to reveal answer
We can convert from rectangular form to polar form by using the following identities:  and
and  . Given
. Given  , then
, then  .
.
 . Dividing both sides by
. Dividing both sides by  ,
,




We can convert from rectangular form to polar form by using the following identities: 





← Didn't Know|Knew It →
What is the equation  in polar form?
in polar form?
What is the equation 
Tap to reveal answer
We can convert from rectangular form to polar form by using the following identities:  and
and  . Given
. Given  , then
, then  . Multiplying both sides by
. Multiplying both sides by  ,
,



We can convert from rectangular form to polar form by using the following identities: 




← Didn't Know|Knew It →
Convert the following function into polar form:

Convert the following function into polar form:
Tap to reveal answer
The following formulas were used to convert the function from polar to Cartestian coordinates:

Note that the last formula is a manipulation of a trignometric identity.
Simply replace these with x and y in the original function.



The following formulas were used to convert the function from polar to Cartestian coordinates:
Note that the last formula is a manipulation of a trignometric identity.
Simply replace these with x and y in the original function.
← Didn't Know|Knew It →
What is the equation  in polar form?
in polar form?
What is the equation 
Tap to reveal answer
We can convert from rectangular to polar form by using the following trigonometric identities:  and
and  . Given
. Given  , then:
, then:


Dividing both sides by  , we get:
, we get:




We can convert from rectangular to polar form by using the following trigonometric identities: 


Dividing both sides by 
← Didn't Know|Knew It →
What is the polar form of  ?
?
What is the polar form of 
Tap to reveal answer
We can convert from rectangular to polar form by using the following trigonometric identities: 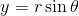 and
and  . Given
. Given  , then:
, then:


Dividing both sides by 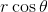 , we get:
, we get:




We can convert from rectangular to polar form by using the following trigonometric identities: and
. Given

Dividing both sides by , we get:
← Didn't Know|Knew It →
What is the polar form of  ?
?
What is the polar form of 
Tap to reveal answer
We can convert from rectangular to polar form by using the following trigonometric identities: 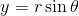 and
and  . Given
. Given  , then:
, then:

Dividing both sides by 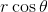 , we get:
, we get:




We can convert from rectangular to polar form by using the following trigonometric identities: and
. Given

Dividing both sides by , we get:
← Didn't Know|Knew It →
What is the polar form of  ?
?
What is the polar form of 
Tap to reveal answer
We can convert from rectangular to polar form by using the following trigonometric identities: 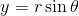 and
and  . Given
. Given  , then:
, then:




We can convert from rectangular to polar form by using the following trigonometric identities: and
. Given

← Didn't Know|Knew It →







