Estimating Limits from Graphs and Tables - AP Calculus BC
Card 1 of 170

Given the above graph of  , what is
, what is  ?
?

Given the above graph of 

Tap to reveal answer
Examining the graph, we can observe that ") does not exist, as  is not continuous at
is not continuous at 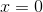 . We can see this by checking the three conditions for which a function
. We can see this by checking the three conditions for which a function  is continuous at a point
is continuous at a point 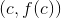 :
:
- A value
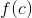 exists in the domain of
exists in the domain of 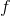
- The limit of
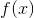 exists as
exists as 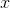 approaches
approaches 
- The limit of
 at
at  is equal to
is equal to 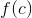
Given  , we can see that condition #1 is not satisfied because the graph has a vertical asymptote instead of only one value for
, we can see that condition #1 is not satisfied because the graph has a vertical asymptote instead of only one value for 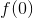 and is therefore an infinite discontinuity at
and is therefore an infinite discontinuity at 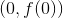 .
.
We can also see that condition #2 is not satisfied because ") approaches two different limits: from the left and
from the left and  from the right.
from the right.
Based on the above, condition #3 is also not satisfied because ") is not equal to the multiple values of 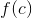 .
.
Thus, ") does not exist.
Examining the graph, we can observe that ") does not exist, as is not continuous at
. We can see this by checking the three conditions for which a function
is continuous at a point
:
- A value
exists in the domain of
- The limit of
exists as
approaches
- The limit of
at
is equal to
Given , we can see that condition #1 is not satisfied because the graph has a vertical asymptote instead of only one value for
and is therefore an infinite discontinuity at
.
We can also see that condition #2 is not satisfied because ") approaches two different limits: from the left and
from the right.
Based on the above, condition #3 is also not satisfied because ") is not equal to the multiple values of .
Thus, ") does not exist.
← Didn't Know|Knew It →

Given the graph of  above, what is
above, what is  ?
?

Given the graph of 

Tap to reveal answer
Examining the graph of the function above, we need to look at three things:
-
What is the limit of the function as it approaches zero from the left?
-
What is the limit of the function as it approaches zero from the right?
-
What is the function value at zero and is it equal to the first two statements?
If we look at the graph we see that as  approaches zero from the left the
approaches zero from the left the  values approach zero as well. This is also true if we look the values as
values approach zero as well. This is also true if we look the values as  approaches zero from the right. Lastly we look at the function value at zero which in this case is also zero.
approaches zero from the right. Lastly we look at the function value at zero which in this case is also zero.
Therefore, we can observe that  as
as  approaches
approaches  .
.
Examining the graph of the function above, we need to look at three things:
-
What is the limit of the function as it approaches zero from the left?
-
What is the limit of the function as it approaches zero from the right?
-
What is the function value at zero and is it equal to the first two statements?
If we look at the graph we see that as 


Therefore, we can observe that 


← Didn't Know|Knew It →

Given the graph of  above, what is
above, what is  ?
?

Given the graph of 

Tap to reveal answer
Examining the graph above, we need to look at three things:
-
What is the limit of the function as  approaches zero from the left?
approaches zero from the left?
-
What is the limit of the function as  approaches zero from the right?
approaches zero from the right?
-
What is the function value as  and is it the same as the result from statement one and two?
and is it the same as the result from statement one and two?
Therefore, we can determine that  does not exist, since
does not exist, since  approaches two different limits from either side :
approaches two different limits from either side :  from the left and
from the left and  from the right.
from the right.
Examining the graph above, we need to look at three things:
-
What is the limit of the function as
approaches zero from the left?
-
What is the limit of the function as
approaches zero from the right?
-
What is the function value as
and is it the same as the result from statement one and two?
Therefore, we can determine that 



← Didn't Know|Knew It →

Given the above graph of  , what is
, what is  ?
?
Given the above graph of 

Tap to reveal answer
Examining the graph, we want to find where the graph tends to as it approaches zero from the right hand side. We can see that there appears to be a vertical asymptote at zero. As the x values approach zero from the right the function values of the graph tend towards positive infinity.
Therefore, we can observe that  as
as  approaches
approaches  from the right.
from the right.
Examining the graph, we want to find where the graph tends to as it approaches zero from the right hand side. We can see that there appears to be a vertical asymptote at zero. As the x values approach zero from the right the function values of the graph tend towards positive infinity.
Therefore, we can observe that 


← Didn't Know|Knew It →

Tap to reveal answer
← Didn't Know|Knew It →

Tap to reveal answer
← Didn't Know|Knew It →

Tap to reveal answer
← Didn't Know|Knew It →

Tap to reveal answer
← Didn't Know|Knew It →

Tap to reveal answer
← Didn't Know|Knew It →

Tap to reveal answer
← Didn't Know|Knew It →

Tap to reveal answer
← Didn't Know|Knew It →

Tap to reveal answer
← Didn't Know|Knew It →

Tap to reveal answer
← Didn't Know|Knew It →

Tap to reveal answer
← Didn't Know|Knew It →

Tap to reveal answer
← Didn't Know|Knew It →

Tap to reveal answer
← Didn't Know|Knew It →
For the piecewise function:
 , find
, find  .
.
For the piecewise function:


Tap to reveal answer
The limit  indicates that we are trying to find the value of the limit as
indicates that we are trying to find the value of the limit as  approaches to zero from the right side of the graph.
approaches to zero from the right side of the graph.
From right to left approaching  , the limit approaches to 1 even though the value at
, the limit approaches to 1 even though the value at  of the piecewise function does not exist.
of the piecewise function does not exist.
The answer is  .
.
The limit 

From right to left approaching 

The answer is 
← Didn't Know|Knew It →
For the piecewise function:
 , find
, find  .
.
For the piecewise function:


Tap to reveal answer
The limit  indicates that we are trying to find the value of the limit as
indicates that we are trying to find the value of the limit as  approaches to zero from the right side of the graph.
approaches to zero from the right side of the graph.
From right to left approaching  , the limit approaches to 1 even though the value at
, the limit approaches to 1 even though the value at  of the piecewise function does not exist.
of the piecewise function does not exist.
The answer is  .
.
The limit 

From right to left approaching 

The answer is 
← Didn't Know|Knew It →

Given the graph of  above, what is
above, what is  ?
?

Given the graph of 

Tap to reveal answer
Examining the graph of the function above, we need to look at three things:
-
What is the limit of the function as it approaches zero from the left?
-
What is the limit of the function as it approaches zero from the right?
-
What is the function value at zero and is it equal to the first two statements?
If we look at the graph we see that as  approaches zero from the left the
approaches zero from the left the  values approach zero as well. This is also true if we look the values as
values approach zero as well. This is also true if we look the values as  approaches zero from the right. Lastly we look at the function value at zero which in this case is also zero.
approaches zero from the right. Lastly we look at the function value at zero which in this case is also zero.
Therefore, we can observe that  as
as  approaches
approaches  .
.
Examining the graph of the function above, we need to look at three things:
-
What is the limit of the function as it approaches zero from the left?
-
What is the limit of the function as it approaches zero from the right?
-
What is the function value at zero and is it equal to the first two statements?
If we look at the graph we see that as 


Therefore, we can observe that 


← Didn't Know|Knew It →

Given the graph of  above, what is
above, what is  ?
?

Given the graph of 

Tap to reveal answer
Examining the graph above, we need to look at three things:
-
What is the limit of the function as  approaches zero from the left?
approaches zero from the left?
-
What is the limit of the function as  approaches zero from the right?
approaches zero from the right?
-
What is the function value as  and is it the same as the result from statement one and two?
and is it the same as the result from statement one and two?
Therefore, we can determine that  does not exist, since
does not exist, since  approaches two different limits from either side :
approaches two different limits from either side :  from the left and
from the left and  from the right.
from the right.
Examining the graph above, we need to look at three things:
-
What is the limit of the function as
approaches zero from the left?
-
What is the limit of the function as
approaches zero from the right?
-
What is the function value as
and is it the same as the result from statement one and two?
Therefore, we can determine that 



← Didn't Know|Knew It →























