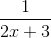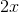Using e
Help Questions
Algebra 2 › Using e
Simplify:
Explanation
In order to eliminate the natural log on both side, we will need to raise both sides as a power with a base of 
The equation will become:
Subtract 
Simplify both sides.
Divide both sides by negative five.
The answer is:
Simplify:
Explanation
In order to solve for the x-variable, we will need to raise both sides as powers of base 

The equation becomes:
Add three on both sides.
Divide by four on both sides.
The equation is:
The answer is:
Solve for
Explanation
Step 1: Achieve same bases
Step 2: Drop bases and set exponents equal to eachother
Step 3: Solve for
Solve for
Explanation
Step 1: Achieve same bases
Step 2: Drop bases and set exponents equal to eachother
Step 3: Solve for
Simplify:
Explanation
In order to get rid of the natural log, we will need to use the exponential term 
The equation becomes:
Subtract nine from both sides.
Divide by three on both sides.
Simplify both sides.
The answer is:
Solve for
Explanation
Step 1: Achieve same bases
Step 2: Drop bases, set exponenets equal to eachother
Step 3: Solve for
Simplify:
Explanation
In order to cancel the natural logs, we will need to use 
The equation becomes:
Subtract 
The equation becomes:
Use the quadratic equation to solve for the possible roots.
Simplify the quadratic equation.
The answers are:
Solve for
Explanation
Step 1: Achieve same bases
Step 2: Drop bases, set exponents equal to eachother
Step 3: Solve for x
Solve:
The answer does not exist.
Explanation
To solve 

Since 


The answer is:
Solve for
Explanation
Step 1: Achieve same bases
Step 2: Drop bases, set exponents equal to eachother
Step 3: Solve for





















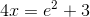


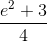




























































![2x-3 -[2x]+(3)=x^2-[2x]+(3)](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/840260/gif.latex)