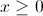Algebra II - Solving Inequalities

Solve for :

$3(x + 4) \leq x - 6$

$x \leq -9$

$x \leq 9$

$x \geq -9$

$x \geq 9$

$x \leq 3$

Explanation

The first step is to distribute (multiply) through the parentheses:

$3(x + 4) \leq x - 6$

$3x + 12 \leq x - 6$

Then subtract from both sides of the inequality:

$2x + 12 \leq -6$

Next, subtract the 12:

$2x \leq -18$

Finally, divide by two:

$x \leq -9$

Solve the inequality:

$\small x^2+4< 9$

$\small -\sqrt5< x< \sqrt5$

$\small x< \sqrt5$

$\small x< -\sqrt5$

$\small -\sqrt5> x\ or\ x> \sqrt5$

Explanation

$\small \small x^2+4< 9$

$\small x^2< 5$

$\small x< \left | (\pm\sqrt5) \right |$

$\small -\sqrt5< x< \sqrt5$

Solve for :

$5-3x\leq14$

$x\geq-3$

$x\geq3$

$x\geq9$

$x\leq3$

$x\geq0$

Explanation

Inequalities can be treated like any other equation except when multiplying and dividing by negative numbers. When multiplying or dividing by negative numbers, we just flip the sign of the inequality so that becomes , and vice versa.

$5-3x\leq14$

$-3x\leq9$

$\frac{-3x}{-3}\geq\frac{9}{-3}$

$x\geq-3$

Solve the inequality:

$x<-\frac{1}{18}$

$x>-\frac{1}{18}$

$\textup{No solution.}$

$x<-\frac{15}{18}$

$x>-\frac{15}{18}$

Explanation

Add on both sides to avoid dividing by a negative later in the calculation. Dividing by a negative value will require switching the sign.

The inequality becomes:

Subtract 8 from both sides.

Divide by 18 on both sides.

$\frac{-1}{18}>\frac{18x}{18}$

The answer is: $x<-\frac{1}{18}$

Solve this inequality.

$\left | \frac{4x+3}{x+6}\right |\eq>1$

$x \eq< -\frac{9}{5}, \hspace x \eq>1$

$x\eq>-\frac{9}{5}, x \eq<1$

$x\eq>-\frac{9}{5}, x\eq>1$

$x<-\frac{9}{5}, x\eq<1$

$x\eq<\frac{9}{5}, x\eq>-1$

Explanation

Split the inequality into two possible cases as follows, based on the absolute values.

First case: $\frac{4x+3}{x+6}\eq>1$

Second case: $\frac{4x+3}{x+6} \eq< -1$

Let's find the inequality of the first case.

$\frac{4x+3}{x+6} \eq>1$

Multiply both sides by x + 6.

$4x+3 \eq>x+6$

Subtract x from both sides, then subtract 3 from both sides.

$3x \eq>3$

Divide both sides by 3.

$x\eq>1$

Let's find the inequality of the second case.

$\frac{4x+3}{x+6} \eq< -1$

Multiply both sides by x + 6.

$4x+3 \eq< -1(x+6)$

Simplify.

Add x to both sides, then subtract 3 from both sides.

$5x\eq< -9$

Divide both sides by 5.

$x \eq<-\frac{9}{5}$

So the range of x-values is $x<-\frac{9}{5}$ and $x \eq>1$ .

Solve the following inequality for :

$\large -7x-2 \ge 12$

$x \le -2$

$\large x \ge -2$

$\large x \ge 2$

Explanation

Most of solving inequalities is straightforward algebra and we can manipulate them in the same way as equations in most cases.

$\large -7x-2 \ge 12$

$\large -7x \ge 14$

However, we must remember that when multiplying or dividing by negative numbers in inequalities, we have to switch the direction of the inequality. So we do the final division step and get the answer:

$\large x \le -2$

Solve the inequality for

$-2\leq \frac{1-3x}{4}\leq 4$

$-5\leq x\leq3$

$3\leq x\leq -5$

$3\leq x\leq 7$

$-5\leq x \leq 7$

$5\leq x \leq -7$

Explanation

$-2\leq \frac{1-3x}{4}\leq 4$

Inequalities can be algebraically rearranged using operations that are mostly identical to algebraic equations, although one notable exception is multiplication or division by -1. This reverses the inequality signs.

Multiply out by