Median
Help Questions
Algebra 2 › Median
Determine the median of the numbers:
Explanation
The numbers are already provided in chronological order.
The median of an even number of data is the average of the two central numbers of the data set.
Take the average of the two numbers.
The answer is:
Determine the median:
Explanation
Reorder the numbers from least to greatest.
The median of an even set of data is the average of the center two numbers in a chronological ordered set of numbers.
Average the two numbers.
The answer is:
What is the median of the following numbers?
12,15,93,32,108,22,16,21
Explanation
To find the median, first you arrange the numbers in order from least to greatest.
Then you count how many numbers you have and divide that number by two. In this case 12,15,16,21,22,32,93,108= 8 numbers.
So
Then starting from the least side of the numbers count 4 numbers till you reach the median number of
Then starting from the greatest side count 4 numbers until you reach the other median number of
Finally find the mean of the two numbers by adding them together and dividing them by two
to find the median number of 
Consider the following test scores from a typical high school class with 
The mean of this data set is , and the mode of this data set is .
Explanation
The mean is just the average of all the test scores, which is found by adding up the scores and dividing by the number of scores (



Find the median of the following numbers:
11, 13, 16, 13, 14, 19, 13, 13
None of the other answers are correct.
Explanation
Reorder the numbers in ascending order (from lowest to highest):
11, 13, 13, 13, 13, 14, 16, 19
Find the middle number. In this case, the middle number is the average of the 4th and 5th numbers. Because both the 4th and 5th number are 13, the answer is simply 13.
Find the median of the following data set:
Explanation
Find the median of the following data set:
Let's begin by putting our data in increasing order:
Now, the median should be pretty straightforward to find.
The median will simply be the number in the middle of all the terms.
In this case, it is the number in red below
So our answer is 67.
Determine the median of the numbers:
Explanation
In order to determine the median, we will need to rearrange the data set from least to greatest.
Since there is an even amount of numbers, the median is the average of the two central numbers.
The answer is:
A student has taken five algebra tests already this year. Her scores were 




Explanation
To find the median of a set of values, simply place the numbers in order and find the value that is exactly "in the middle." Here, we can place the test scores in ascending order to get 





Find the median:
Explanation
First regroup all numbers in chronological order.
Since there is an even amount of numbers in the dataset, 6 numbers total, the median will be the average of the third and fourth numbers.
Find the mean of the two numbers.
What is the median of the first six cubic numbers?
Explanation
Cubic numbers are numbers taken to the third power. The first six cubic numbers are: 

Since, the numbers are inceasing, count the numbers in the set. There are six. Then divide six by two. We do this because we will split the number set in half. Because six does divide evenly into two, this means we can't easily determine the median. Since six divided by two is three, we are going to eliminate three numbers from leftmost in number set toward the right direction and three numbers from rightmost in number set toward the left direction. The last number crossed out in both direction are 


![[-10,-3,9,14,26,1000]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/862606/gif.latex)







![[-3,-9,27,18]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/815527/gif.latex)





![[-3,-9,27,18]\rightarrow [ -9,-3,18,27]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/815528/gif.latex)












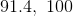


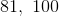












![[-1,-3,1,0,1,10]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/793642/gif.latex)





![[-1,-3,1,0,1,10]\rightarrow[-3,-1,0,1,1,10]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/793643/gif.latex)







![a=[-5,-1-1,0,-2,-9]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/549904/gif.latex)





![a=[-5,-1-1,0,-2,-9] = [-9,-5,-2,-1,-1,0]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/549905/gif.latex)





