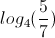Logarithms
Help Questions
Algebra II › Logarithms
Solve 
Explanation
First we start by subtracting 
Next, we rewrite the equation in exponent form:
Finally, we divide by 
Simplify the expression using logarithmic identities.
The expression cannot be simplified
Explanation
The logarithm of a fraction is equal to the logarithm of the numerator minus the logarithm of the denominator.
If we encounter two logarithms with the same base, we can likely combine them. In this case, we can use the reverse of the above identity.
Simplify the expression using logarithmic identities.
The expression cannot be simplified
Explanation
The logarithm of a fraction is equal to the logarithm of the numerator minus the logarithm of the denominator.
If we encounter two logarithms with the same base, we can likely combine them. In this case, we can use the reverse of the above identity.
Solve the following:
Explanation
When the base isn't explicitly defined, the log is base 10. For our problem, the first term
is asking:
For the second term,
is asking:
So, our final answer is
Solve:
Explanation
Change the base of the inner term or log to base ten.
According to the log property:
The log based ten and the ten to the power of will cancel, leaving just the power.
The answer is:
Solve the following:
Explanation
When the base isn't explicitly defined, the log is base 10. For our problem, the first term
is asking:
For the second term,
is asking:
So, our final answer is
Solve:
Explanation
Change the base of the inner term or log to base ten.
According to the log property:
The log based ten and the ten to the power of will cancel, leaving just the power.
The answer is:
Which is another way of expressing

Explanation
Use the rule:
therefore
Add the logarithms:
Explanation
When adding logarithms of the same base, all you have to do is multiply the numbers inside the function as shown below:
Add the logarithms:
Explanation
When adding logarithms of the same base, all you have to do is multiply the numbers inside the function as shown below: