Fractional Exponents
Help Questions
Algebra 2 › Fractional Exponents
Evaluate
Explanation
When dealing with fractional exponents, we rewrite as such:
in which 


Evaluate
Explanation
When dealing with fractional exponents, remember this form:
![\sqrt[a]{x^n}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/572997/gif.latex)



Evaluate
Explanation
When dealing with fractional exponents, remember this form:
![\sqrt[a]{x^n}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/573029/gif.latex)



Evaluate
Explanation
When dealing with fractional exponents, we rewrite as such:
in which 


Write 
Explanation
Fractional exponents are an alternate way to write a radical expression. The numerator of the fractional exponent becomes the exponent of the term inside the radical and the denominator of the fractional exponent determines the index of the radical.
So 
![\sqrt[5]{x^{2}}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/716923/gif.latex)
Simplify:
Explanation
When dealing with fractional exponents, we rewrite as such: ![x^{\frac{a}{b}}=\sqrt[b]{x^a}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/695410/gif.latex)



Find the value of
Explanation
When you have a number or value with a fractional exponent,
or
So then,
Simplify the expression:
Explanation
Remember that fraction exponents are the same as radicals.
A shortcut would be to express the terms as exponents and look for opportunities to cancel.
Either method, we then need to multiply to two terms.
Which of the following is equivalent to 
Explanation
Which of the following is equivalent to 
When dealing with fractional exponents, keep the following in mind: The numerator is making the base bigger, so treat it like a regular exponent. The denominator is making the base smaller, so it must be the root you are taking.
This means that 

![\sqrt[5]{b}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/559668/gif.latex)
So if we put it together we get:
Evaluate
Explanation
When dealing with fractional exponents, remember this form:
![\sqrt[a]{x^n}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/573003/gif.latex)









![x^\frac{a}{b}=\sqrt[b]{x^a}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/707002/gif.latex)







![2^{\frac{1}{2}}=\sqrt[2]{2^1}=\sqrt{2}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/573001/gif.latex)

![\sqrt[3]{3}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/572960/gif.latex)



![\frac{\sqrt[3]{3}}{3}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/572964/gif.latex)
![3^{\frac{1}{3}}=\sqrt[3]{3^1}=\sqrt[3]{3}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/573033/gif.latex)

![\sqrt[3]{324}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/706986/gif.latex)


![\sqrt[3]{54}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/706989/gif.latex)

![x^\frac{a}{b}=\sqrt[b]{x^a}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/707033/gif.latex)
![18^\frac{2}{3}=\sqrt[3]{18^2}=\sqrt[3]{324}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/707037/gif.latex)
![\sqrt[5]{x^{2}}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/716826/gif.latex)
![\sqrt[]{x^{5}}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/716827/gif.latex)
![\frac{1}{\sqrt[5]{x^{2}}}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/716828/gif.latex)

![2\sqrt[5]{x}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/716830/gif.latex)

![\sqrt[8]{3}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/695279/gif.latex)

![\frac{1}{\sqrt[8]{3}}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/695281/gif.latex)


![3^{\frac{1}{8}}=\sqrt[8]{3}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/695414/gif.latex)





![x^{\frac{a}{b}}=\sqrt[b]{x^a}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/329490/gif.latex)
![x^{\frac{a}{b}}=(\sqrt[b]{x})^a](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/329491/gif.latex)
![64^{\frac{4}{3}}=\sqrt[3]{64^4}=\sqrt[3]{2^{24}}=2^8=256](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/329492/gif.latex)

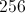




![256^{\frac{3}{4}}=\sqrt[4]{256^3}=64](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/113588/gif.latex)



![\sqrt[5]{b^4}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/559586/gif.latex)
![\sqrt[4]{b^5}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/559587/gif.latex)
![\sqrt[4]{b^{-5}}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/559588/gif.latex)

![\sqrt[5]{b^4}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/559669/gif.latex)

![\sqrt[3]{16}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/572971/gif.latex)


![\frac{\sqrt[3]{4}}{2}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/572974/gif.latex)
![\frac{\sqrt[3]{16}}{2}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/572975/gif.latex)
![4^{\frac{2}{3}}=\sqrt[3]{4^2}=\sqrt[3]{16}](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/573007/gif.latex)