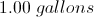Algebra II - Direct Proportionality

The distance of a cyclist is directly proportional to the time he has traveled. Suppose he has traveled 12 miles in 1.5 hours. How far does he travel in a half hour?

Explanation

Write the equation for direct proportionality.

$y=kx \rightarrow D=kT$

Substitute the distance and time given to solve for the constant of proportionality, .

Divide by 1.5 on both sides.

$\frac{12}{1.5} = \frac{k(1.5)}{1.5}$

Write the equation.

Substitute half an hour for the time to determine the distance the biker has traveled.

The biker traveled four miles in a half hour.

The answer is:

Sarah notices her map has a scale of $\frac{1}{4}; in=1; mile$ . She measures between Beaver Falls and Chipmonk Cove. How far apart are the cities?

Explanation

$\frac{1}{4}; in=1; mile$ is the same as

So to find out the distance between the cities

$12.5; in \cdot \frac{4; miles}{1;in }=50; miles$

If an object is hung on a spring, the elongation of the spring varies directly as the mass of the object. A 20 kg object increases the length of a spring by exactly 7.2 cm. To the nearest tenth of a centimeter, by how much does a 32 kg object increase the length of the same spring?

$11.5 \textrm{ cm}$

$4.5 \textrm{ cm}$

$18.4 \textrm{ cm}$

$9.1\textrm{ cm}$

$8.4 \textrm{ cm}$

Explanation

Let be the mass of the weight and the elongation of the spring. Then for some constant of variation ,

We can find by setting from the first situation:

$7.2 = k \cdot 20$

$k = 7.2 \div 20 = 0.36$

In the second situation, we set and solve for :

$L = 0.36 \cdot32 =11.52$

which rounds to 11.5 centimeters.

There are two similar buckets of cylindrical shape. Bucket A has a height of and a radius of . Bucket B has a height of . How much can Bucket B hold?

$14.14ft^{3}$

$11.86ft^{3}$

$8.57ft^{3}$

$9.42ft^{3}$

$1.77ft^{3}$

Explanation

First, we need to find the radius of Bucket B by setting up a proportion:

$\frac{.75ft}{1ft}=\frac{r}{2ft}$

Now we can plug the radius into the formula for the volume of a cylinder:

$V=\pi r^{2}h$

$V=\pi (1.5ft)^{2}(2ft)$

If an object is hung on a spring, the elongation of the spring varies directly with the mass of the object. A 33 kilogram object increases the length of a spring by exactly 6.6 centimeters. To the nearest tenth of a kilogram, how much mass must an object posess to increase the length of that same spring by exactly 10 centimeters?

$50 \textrm{ kg}$

$100 \textrm{ kg}$

$200 \textrm{ kg}$

$80 \textrm{ kg}$

$40 \textrm{ kg}$

Explanation

Let be the mass of the weight and the elongation of the spring, respectively. Then for some constant of variation ,

We can find by setting :

$6.6 = k \cdot 33$

$k = 6.6 \div 33 = 0.2$

Therefore .

Set and solve for :

$M = 10 \div 0.2 = 50$ kilograms

Sally currently has 192 books. Three months ago, she had 160 books. By what percentage did her book collection increase over the past three months?

Explanation

To find the percentage increase, divide the number of new books by the original amount of books:

She has 32 additional new books; she originally had 160.

$\frac{32}{160} = \frac{16}{80} = 0.20=20%$

The quantity x varies directly with y. If x is 26 when y is 100, find x when y is 200.

104

6.5

Explanation

We must set up a proportion. Since x varies directly with y, when y is multiplied by 2, x is also multiplied by 2. 26 times 2 is 52.

Direct variation: $\frac{x_1}{x_2}=\frac{y_1}{y_2}$

$\frac{26}{x_2}=\frac{100}{200}$

$\frac{26}{x_2}=\frac{1}{2}$

On a map of the United States, Mark notices a scale of $\small in = 250$ . If the distance between New York City and Los Angeles in real life is , how far would the two cities be on Mark's map?

Explanation

If the real distance between the two cities is , and = , then we can set up the proportional equation:

$\frac{1 in}{250 miles}=\frac{xin}{2400 miles}$

Sunshine paint is made by mixing three parts yellow paint and one part red paint. How many gallons of yellow paint should be mixed with two quarts of red paint?

(1 gallon = 4 quarts)

Explanation

First set up the proportion:

$\frac{3; parts ; yellow}{1 ; part; red}=\frac{x ; quarts ; yellow}{2 ; quarts ; red}$

x =

Then convert this to gallons:

$6 ; quarts; \cdot \frac{1 ; gallon}{4; quarts}= 1.50; gallons$

A man wants to find the height of a building. Being unable to climb the building to measure its height directly, he waits until it's a sunny day and stands so that the top of his shadow lines up with the top of the building's shadow. He know's that he's tall, and that he's from where the shadows stop. He them measures that he's from the edge of the building. What is the building's height?

Explanation

First, let's make the height of the building . We're looking for a ratio of the height of the object to the length of its shadow. For the man, we know both of these things, so we can express the ratio:

$\frac{6ft}{4ft}$

We don't know the building's height, so let's just use as a stand-in for the ratio for now. Also, the length of the building's shadow is the length of the man's shadow plus the distance he is from the building: