Arithmetic Series
Help Questions
Algebra 2 › Arithmetic Series
A sequence begins as follows:
Which statement is true?
The sequence may be arithmetic.
The sequence may be geometric.
The sequence cannot be arithmetic or geometric.
The sequence may be arithmetic and geometric.
None of these
Explanation
A geometric sequence is one in which each term is generated by multiplying the previous term by the same number - the common ratio. As can be seen here, the ratio of each term to the previous one is not constant:
These ratios can be immediately seen to be unequal as they are of different sign.
An arithmetic sequence is one in which each term is generated by adding the same number - the common difference - to the previous term. As can be seen here, the difference between each term and the previous term is the same:
The sequence could be arithmetic.
A sequence begins as follows:
Which statement is true?
The sequence may be geometric.
The sequence may be arithmetic.
The sequence cannot be arithmetic or geometric.
Explanation
An arithmetic sequence is one in which each term is generated by adding the same number - the common difference - to the previous term. As can be seen here, the differences between each term and the previous term is not constant from term to term:
The sequence cannot be arithmetic.
A geometric sequence is one in which each term is generated by multiplying the previous term by the same number - the common ratio. As can be seen here, the ratio of each term to the previous one is the same:
The sequence could be geometric.
Given the sequence below, what is the sum of the next three numbers in the sequence?
Explanation
By taking the difference between two adjacent numbers in the sequence, we can see that the common difference increases by one each time.
Our next term will fit the equation 

After 


Finally, after 

The question asks for the sum of the next three terms, so now we need to add them together.
What is the common difference of the following arithmetic series?
Explanation
What is the common difference of the following arithmetic series?
To find the common difference, we need to find the difference between any two consecutive terms.
Try with the first two:
To be sure, try it with the 2nd and 3rd
We keep getting the same thing, -8. It must be negative, because our sequence is decreasing. Therefore, we have our answer: -8
Given the sequence: ![[5,11,17,...]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/850736/gif.latex)
Explanation
Write the formula for the arithmetic sequence.
The first term is:
The common difference is the same for each term, which is increasing by six every term:
Substitute and simplify the formula.
To find the hundredth term, plug in 
The answer is:
List the first 4 terms of an arithmetic sequence with a first term of 3, and a common difference of 5.
Explanation
An arithmetic sequence is one in which the common difference is added to one term to get the next term. Thus, if the first term is 3, we add 5 to get the second term, and continue in this manner.
Thus, the first four terms are:
Which number is needed to complete the following sequence:
1,5,_,13,17
Explanation
This is a sequence that features every other positive, odd integers. The missing number in this case is 9.
For the sequence of numbers 
a) An explicit formula for the nth term
b)
a)
b)
a)
b)
a)
b)
a)
b)
a)
b)
Explanation
a) The general formula for an arithmetic sequence of terms 


For the sequence to be a true arithmetic sequence, the common difference must be the same for any two adjacent terms in the sequence.
For our sequence:
and so on...
An explicit formula can now be written,
We can now test this formula for the first few terms (columns 1-3 in the table below).
b) In the table below, columns 4-5 show the calculations for the 


Solve the series:
Explanation
Write the n-th term formula.
The 

The 

Solve for 
Divide by two on both sides.
The formula for n-terms in a arithmetic sequence is:
Substitute the known terms.
The answer is:
Which of the following cannot be three consecutive terms of an arithmetic sequence?
Explanation
In each group of numbers, compare the difference of the second and first terms to that of the third and second terms. The group in which they are unequal is the correct choice.
The last group of numbers is the correct choice.
















































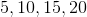







































![\sum_{1}^{n}a_i=(\frac{n}{2})[a_1+a_n]](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/729950/gif.latex)
![(\frac{n}{2})[a_1+a_n] = (\frac{22}{2})[2+44] = (11)(46)=506](https://vt-vtwa-assets.varsitytutors.com/vt-vtwa/uploads/formula_image/image/729951/gif.latex)










